基于任务耦合和角度近似的高精度旋转目标检测
基于任务耦合和角度近似的高精度旋转目标检测¶
介绍一篇最近被 ISPRS&RS接收的遥感旋转目标检测工作:Task Interleaving and Orientation Estimation for High-precision Oriented Object Detection in Aerial Images。该工作讨论了旋转目标检测中分类标签和角度编码的优化。论文实际上是两个子工作的合集,分别涉及了高精度的旋转包围框编码方式以及定位引导的分类标签再划分。介本文只介绍方法思路,详细内容,公式和实现见原论文。
论文地址:https://ming71.github.io/Files/papers/TIOE.pdf
代码:https://github.com/ming71/TIOE
1. Motivation¶
Motivation主要分为两个部分:分类回归的不一致,以及更准确的角度编码,二者最终都是为高精度旋转目标检测服务的。
- 分类回归的不一致问题。
这个话题老生常谈了,如下图中,给出高分类分数的检测结果并不能保证更准确的检测结果;相反,高质量的检测结果可能得到相对低的分类分数。根本原因之一是当前label assignment中multi-candidates的优秀匹配机制导致的。这一机制的好处是:1. 回归收敛更快 (反面教材是最初的yolov3,training epoch是真的多;此外one-to-one match多少也有这个问题)2. 更多的候选框参与回归因而最终输出能有更大的容错。坏处是在高分段的conf中会有明显的分类回归不一致。
通常的检测器通过合适的训练策略能使这些predictions都不太差,因而随便输出一个分类置信不算很低的检测框定位都还算挺准。但是有两个坏处:1. 检测器需要更长训练时间和精妙设计的训练策略以保证高质量的稳定输出(这和收敛快是两码事) 2. 高精度检测结果中性能下降还是很严重。目前主流的遥感旋转目标数据集只统计AP50,IoU在0.5以上皆为良品,这个指标无法反应高精度遥感目标检测性能。

- 分类标签的不准确。
实验中进一步统计了训练过程中检测结果的IoU平均分布及其在所有样本区间的位置。下图中可以发现,其实输出的检测结果中高质量样本确实大有人在,只是通过分类置信我们没有挖掘出来而已。因此需要更加合理的分类分数来引导NMS结果。
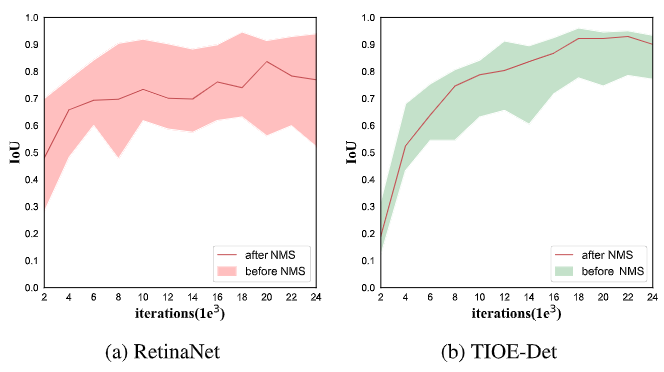
- 更加准确的角度编码。
之前很多类似工作(CSL[1],DCL[2])都讨论过准确的角度预测对旋转目标检测的重要性。尤其是对于具有大宽高比的旋转目标而言,小的角度偏差就能导致很大的IoU下降,因此角度预测尤为重要,对高精度的遥感目标检测更是如此。此外,当前角度表示还存在边角交换性导致的损失跳变等问题也是很常见的(如下图),一些工作中进行了讨论(SCRDet[3],GWD[4], KLD[5],RIDet[6]),感兴趣可以看文末的相关论文不再赘述。
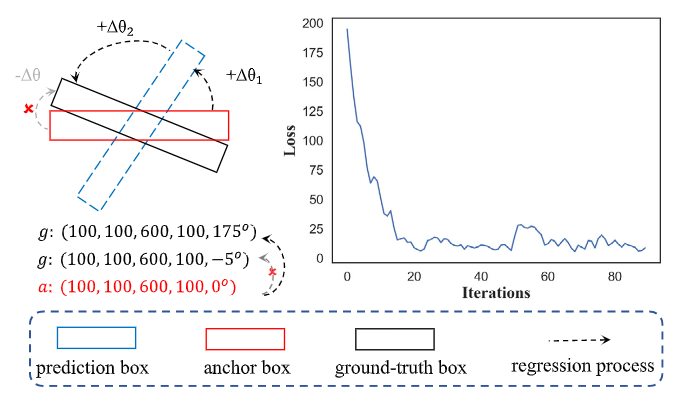
2. Methods¶
2.1 Overview¶
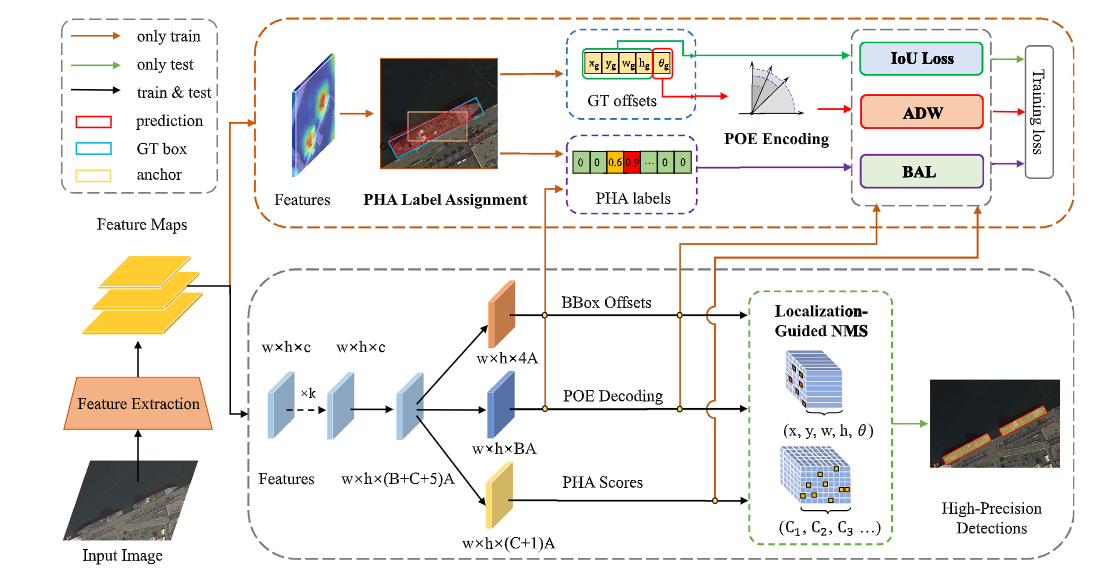
整体的结构图如上所示,TIOEDet主体包含两个部分:PHA label assignment以及POE coding。此外还有基于这两个机制衍生的损失函数和NMS。
2.2 Posterior Hierarchical Alignment Label¶
出发点其实很朴素,就是将定位信息引入分类分数,实现IoU-guided classification就能缓解这个问题。当前的binary labels直接按照设定的IoU阈值给标签,受益最大的metric必然是这个阈值附近的AP。可以认为binary labels是分类回归任务不对齐的祸首之一。为了实现更高精度的识别结果,应该实现连续的定位质量识别,而非仅仅二极管式地一刀切判别。最直观的方式就是将IoU直接加权到分类分数上。但这样有三个问题:
-
IoU代表的语义信息比较模糊,精确的IoU预测比较困难。很多进行IoU预测的模型如IoUNet,MaskScoring RCNN等都用了额外的分支或者专门的训练策略来优化IoU学习,过于麻烦。
-
对低质量样本的准确IoU学习是没必要的。一方面这些样本在IoU学习过程中引入极大的不确定性,海量的困难样本会导致无法收敛;另一方面,界定负样本的定位精度意义不太大,我们需要的是精确的检测结果而不是细致的背景判定。
-
连续IoU的表征会显著加大学习难度,但是带来的性能提升是微乎其微的,如下图,也许IoU为0.5的预测结果相比0.8的看上去差很多,但是IoU为0.8以及0.85的几乎看不出什么区别。IoU的表征粒度和性能增益是边际递减的。
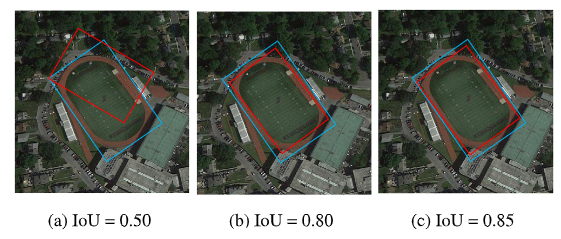
结合上述观察,我们提出了后验层级化的分类标签。这里“后验”指的是输出IoU为导向,区别于以前的输入(anchor)IoU为导向的分数。具体做法就是将正样本的后验IoU区间划成细粒度的分数,我们只学习这些细粒度分数,而不是连续的IoU,给定位信息的预测增大了容错空间;同时相比anchor IoU的分配方式又更加细腻可靠。但是后验IoU信息在训练前期是不可靠的(之前的工作DAL[7]中提过),因此这里借鉴课程学习的方法采用了渐进的粒度增长策略保持稳定的训练结果,逐步提升性能。
进一步,在此基础上将focal loss进行简单改造用于这个分类分支的训练。
推理时,我们就能根据更加准确的分类分数进行可靠的NMS从而实现更好的性能。
2.3 Progressive Orientation Estimation¶
用角度分类实现更加精确的方法在CSL[1]开始已经有一些工作了。角度分类编码代替回归的主要问题集中在:
- 编码没有实际意义,难以学习(如DCL[2]中格雷码性能就是差一截)
- 编码无法度量角度距离。例如,00000和10000只差了一位,但是角度差了很远,角度编码损失无法体现这一点
- 编码的内部重要性度量缺失。例如,八位二进制编码的首位和末尾上,同等的预测偏差造成的数值偏离是大不相同的,现在的方法没有强调这一点。
为了解决上述问题1,我们采用n元码作为角度编码的基础并进行了启发式的解读;对于问题2和3,我们提出了新的损失函数来实现准确的角度损失度量。
首先是n元码的理解,其可以认为是基于区间划分的角度编码方式。如下图,以二进制码为例,在角度编码过程中其物理含义就是对角度定义范围的逐渐二元划分,是对真实角度的逐渐逼近。因此n元码具有一定的可解释性,学习较易。
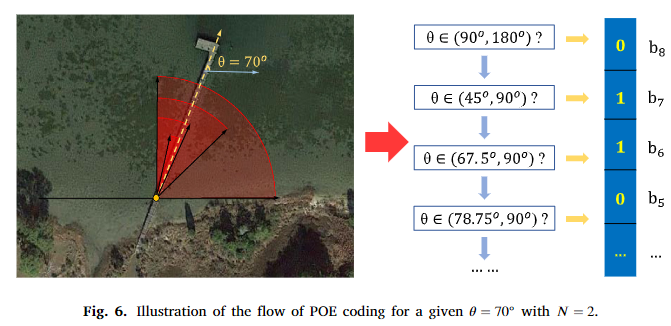
对于角度损失函数,我们针对问题2和问题3分别涉及了不同的模块AOM和EOM:
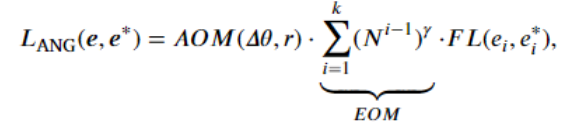
其中,EOM在编码内部不同的位在计算损失时加以不同的权重以区别不同位的影响。后面位的表征都是基于前面的准确预测的,前面的预测出现偏差会导致角度预测大相径庭,后面的位失去意义。但也注意权重设置不能过于畸形,否则模型只关注大区划分而忽略细粒度定位,这就背道而驰了。
AOM则是整体上对角度距离进行了把控和约束。在DCL[2]中的损失函数中也有类似的思想。此外我们在此处考察了宽高比的影响,因为对于越是大ratio的物体角度预测更加重要。AOM函数总结而言应该具有以下优良性质:
- AOM应该是ratio的增函数
- AOM应该是角度误差的增函数
- AOM对角度误差的梯度应该是角度误差的增函数
前两点好理解,第三点是由于角度误差越小,应该保证梯度是逐渐减小或者不变的,否则难以优化。满足上述条件的选择有很多,可以自由发挥。部分结果如下。
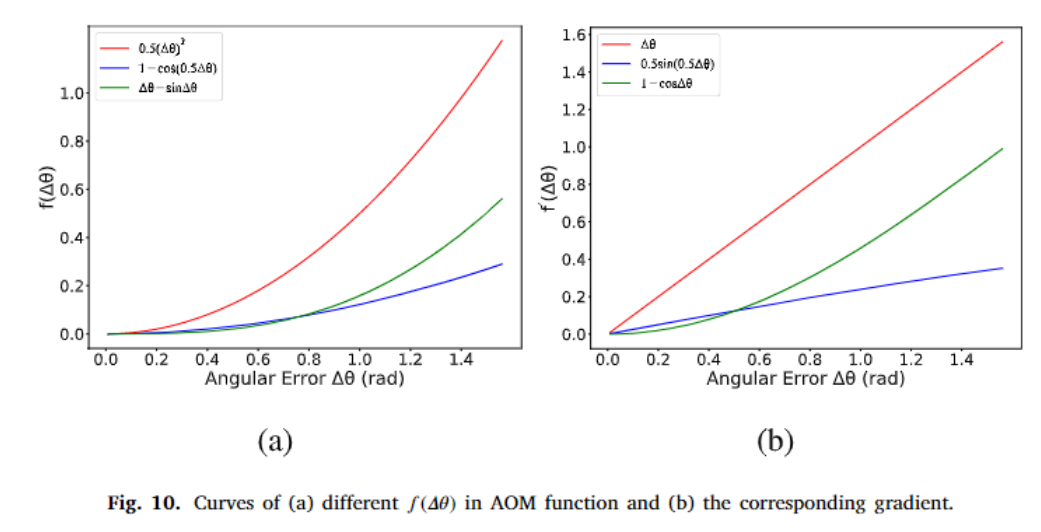
Experiments¶
实验结果部分我们首先通过大量的消融实验逐模块地详细验证了提出方法的有效性。评测指标类似coco采用了AP50:90,同时还用了mAoE来度量角度误差。
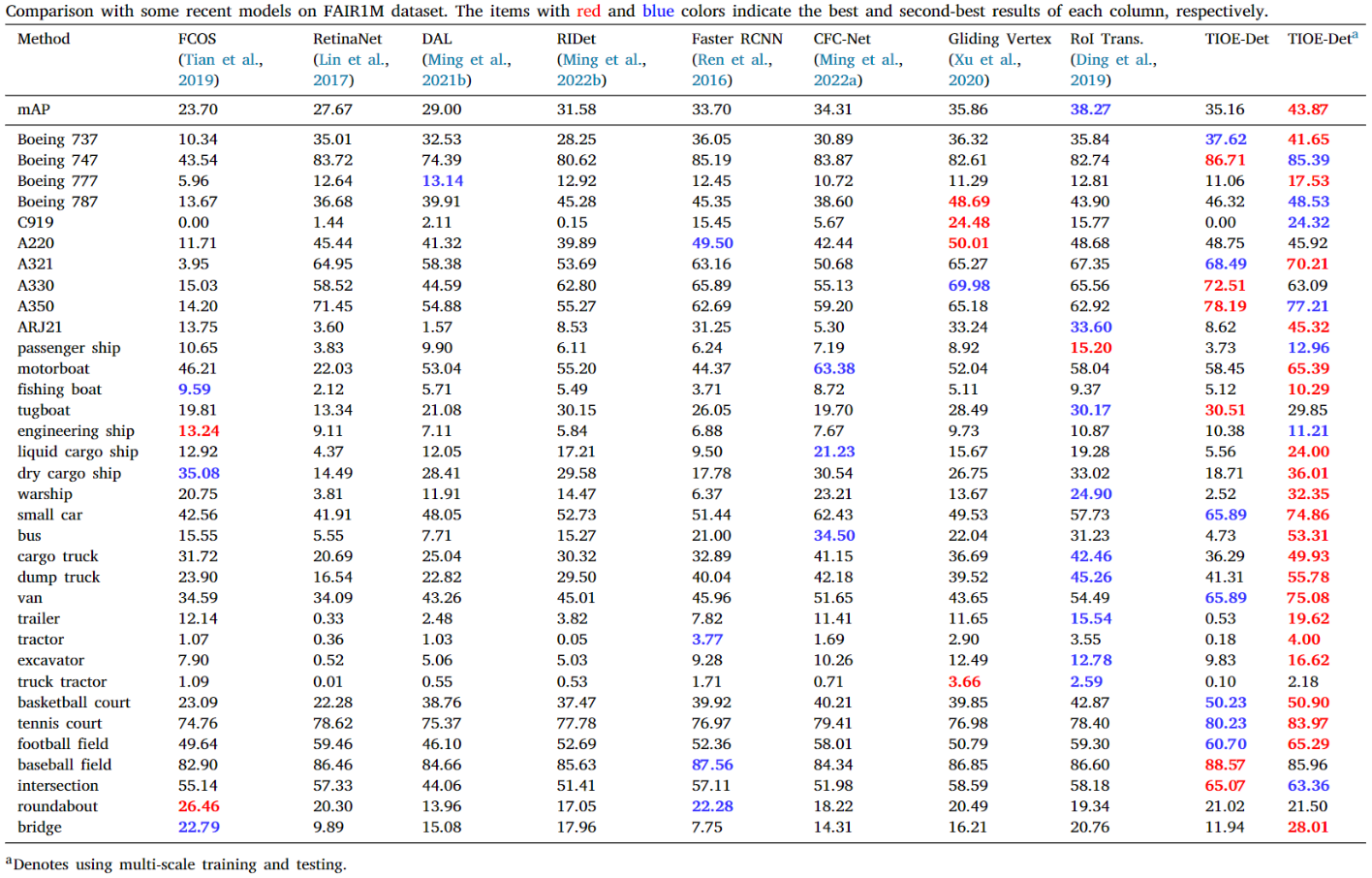
此外,我们在当前主流的遥感数据集上都进行了实验,均能取得不错的效果。也最新的大规模细粒度遥感数据集FAIR1M[8]和DIOR-R[9]上进行了实验。部分结果如下:
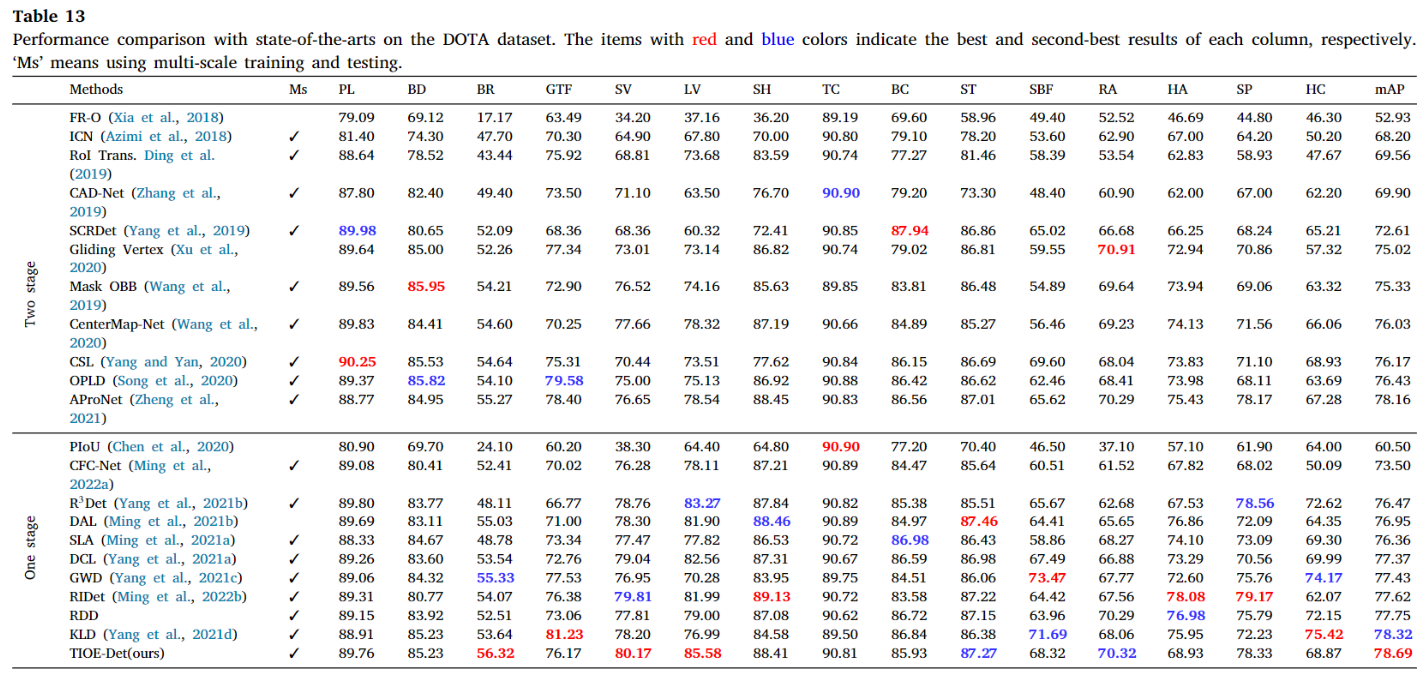

由于之前投会议被质疑方法过于简单偏工程,后面直接合并转期刊了,导致其到发表耗时快两年,实验结果现在已经不算sota(DOTA现在自称sota得上80+),思路仅供借鉴。最后代码基于yolov5-obb实现的,感谢胡凯旋大佬的codebase。贴张检测图:

Reference¶
[1] Yang X, Yan J. Arbitrary-oriented object detection with circular smooth label[C]//Computer Vision–ECCV 2020: 16th European Conference, Glasgow, UK, August 23–28, 2020, Proceedings, Part VIII 16. Springer International Publishing, 2020: 677-694.
[2] Yang X, Hou L, Zhou Y, et al. Dense label encoding for boundary discontinuity free rotation detection[C]//Proceedings of the IEEE/CVF conference on computer vision and pattern recognition. 2021: 15819-15829.
[3] Yang X, Yang J, Yan J, et al. Scrdet: Towards more robust detection for small, cluttered and rotated objects[C]//Proceedings of the IEEE/CVF International Conference on Computer Vision. 2019: 8232-8241.\
[4] Yang X, Yan J, Ming Q, et al. Rethinking rotated object detection with gaussian wasserstein distance loss[C]//International Conference on Machine Learning. PMLR, 2021: 11830-11841.
[5] Yang X, Yang X, Yang J, et al. Learning high-precision bounding box for rotated object detection via kullback-leibler divergence[J]. Advances in Neural Information Processing Systems, 2021, 34: 18381-18394.
[6] Ming Q, Miao L, Zhou Z, et al. Optimization for arbitrary-oriented object detection via representation invariance loss[J]. IEEE Geoscience and Remote Sensing Letters, 2021, 19: 1-5.
[7] Ming Q, Zhou Z, Miao L, et al. Dynamic anchor learning for arbitrary-oriented object detection[C]//Proceedings of the AAAI Conference on Artificial Intelligence. 2021, 35(3): 2355-2363.
[8] Sun X, Wang P, Yan Z, et al. FAIR1M: A benchmark dataset for fine-grained object recognition in high-resolution remote sensing imagery[J]. ISPRS Journal of Photogrammetry and Remote Sensing, 2022, 184: 116-130.
[9] Li K, Wan G, Cheng G, et al. Object detection in optical remote sensing images: A survey and a new benchmark[J]. ISPRS journal of photogrammetry and remote sensing, 2020, 159: 296-307.
本文总阅读量次