深度学习Int8的部署推理原理和经验验证
深度学习Int8的部署推理原理和经验验证¶
论文出处:《Integer Quantization for Deep Learning Inference Principles and Empirical Evaluation》
时间:2020.April
单位:NVIDIA
0.前言¶
这篇paper主要的共享是工程上的经验分享,做了比较充足的实验,基本误差在1%以内,也给出了比较workable的int8量化部署的workflow。而且对以前比较多paper”避而不谈“的mobilenet系列和BERT模型的int8量化做了详尽的实验。
1、Introduction¶
这部分我不一一细说,就总结几点很显而易见的量化的好处:
1、32-bit的乘加变成了8-bit的乘加,同样的硬件单元下可以speed up;
2、32-bit的参数变成了8-bit,显然是model size变小了,需要的空间也变少了,ROM和RAM都减少了;
3、因为内存的要求降低了,对cache的利用率等其他内存系统操作等效率也会提高。
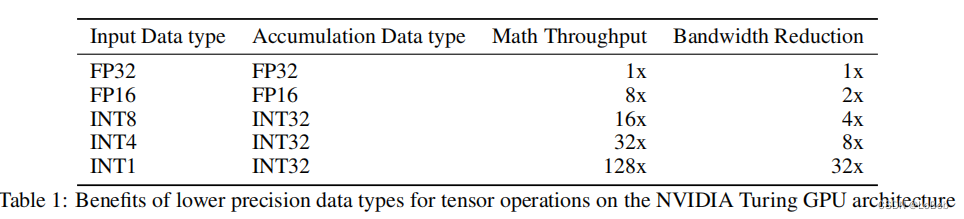
Table 1给出了理论位宽对吞吐、带宽等的要求,有用的信息是累加的数据类型,这一点在做量化部署实现的时候非常重要,其他数值只是个理论值,实际用处不大。
2、相关工作¶
这部分总结得非常好,有必要我也总结一下。
1、《Quantization and training of neural networks for effificient integer-arithmetic-only inference》,也就是做量化必须看的paper,也是tflite的实现,也是目前QAT的做法的主流参考。这篇说的是如何用全整形进行推理,这部分我用c代码全部实现了(下次一定写稿)。
2、《Quantizing deep convolutional networks for effificient inference: A whitepaper》,白皮书,无需多言,必看paper,也是google出品。
3、《 Discovering low-precision networks close to full-precision networks for effificient embedded inference.》这篇说的是,在imagenet上,量化成int8后只需要1个epoch就会恢复到float-32的精度;一个trick即采用退火学习率调度和最后的学习率需要很小;截断阈值采用的百分比的策略。
4、《 Pact: Parameterized clipping activation for quantized neural networks.》,PACT讲的是激活函数的值域范围是可学习的。
然后很多低于8-bit的量化工作,比如1-bit、2-bit等,一些非均匀分布的量化算法(这种实际应用中对速度有比较大的影响,大部分情况都不使用)。
上述基本都是图像领域的,也例举了一些nlp领域的,比如Q8bert。最近关于BERT的量化的工作有以下:Q8BERT、Q-BERT、TernaryBERT、BinaryBERT、BiBERT等。
3、量化基础¶
均分量化即Uniform quantization分两步: 1、选择要量化的数值(浮点)的范围并截断,截断即大于数值范围的就让其为数值范围的最大值,反正就变成数值范围的最小值,min(range_min, max(x, range_max));
2、将截断后的数值映射到整数上,这一步有round的操作。 如图所示:
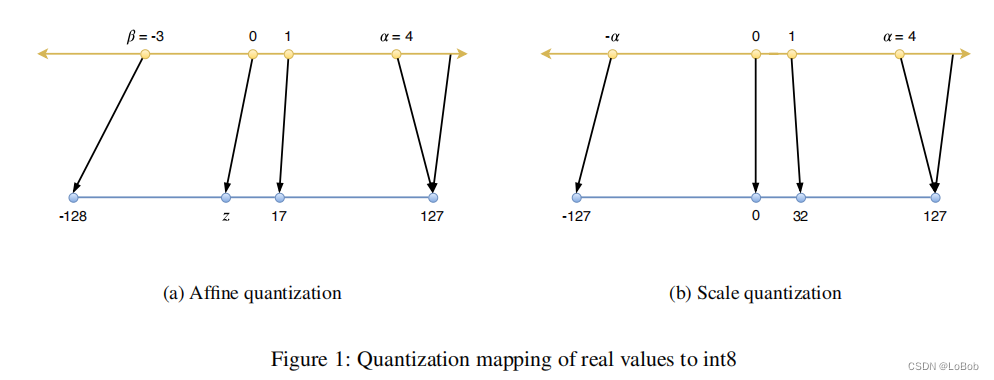
描述在代码和论文中常见的称呼:
Quantize:将一个实数转换为一个量化的整数, 即可float32 变成int8
Dequantize:将一个数从一个量化的整数表示形式转换为一个实数,即int8变成float32
Range Mapping:即一组数值的范围 [β, α]
Affifine Quantization: f(x) = s · x + z ,即非对称量化,s是缩放因子,z是零点,对于int8,那么int8的值域范围就是[0,255]
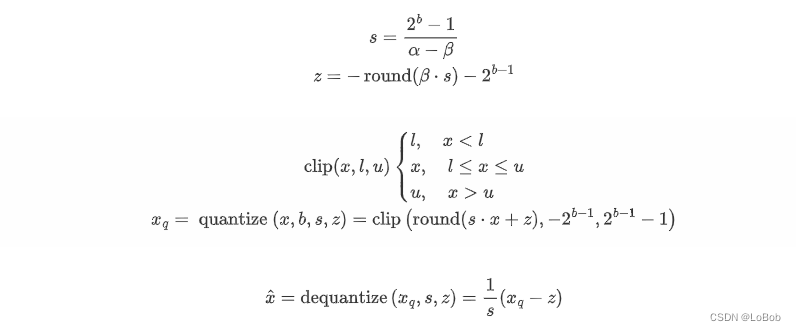
Scale Quantization : f(x) = s · x, 即对称量化,对于int8,那么int8的值域范围就是[-127, 127],不适用128这个数值,原因在IAQ论文说了是为了能用16-bit的累加器来存int8*int8,因为永远不存在-128 × -128,也就是改乘法的结果的绝对值不会超过2^14,可以保证用16-bit的累加器来存这个乘法结果。
Tensor Quantization Granularity:per-tensor & per-channel: 这里更加细致地分析了颗粒度如何从per-tensor变到per-channel,还有中间心态的颗粒度,但实际并不会做太多骚操作,感兴趣的朋友们可以翻原文来了解。per-tensor就是整个神经网络层用一组量化参数(scale, zero-point),per-channel就是一层神经网络每个通道用一组量化参数(scale, zero-point)。那么就是per-channel需要存更多的量化参数,对gemm的计算也有一点影响。
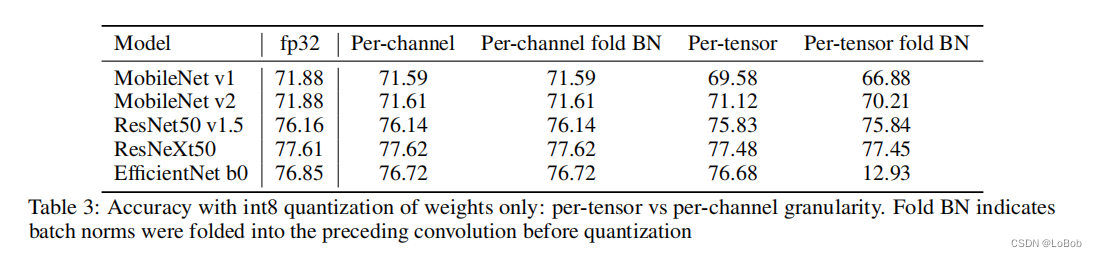
下图表示了这两种颗粒度的实验。值得注意的是,table3的实验是只量化weight的对比实验,可以看到per-channel和per-tensor精度上基本没什么区别,但per-tensor对fold BN在轻量化网络会有比较的性能影响,而per-channel不会有这个情况。
个人观点,这个图并不能下结论:per-channel和per-tensor在int8量化推理下没有太大的差异,因为这只量化weight,而没有考虑其他,比如量化activation。
Affifine Quantization即非对称量化在做矩阵乘法的时候比对称量化多了好几项:
下面是非对称量化的乘法,即y=w × x,这里不考虑bias。
而对称量化的乘法:
多的两项为:
这项可以提前算好,因为w和z的数值是事先知道的。
这项只能运行中计算,因为x是神经网络中的激活值。
那么,实际应用为了提高推理速度,更加愿意用对称量化; 这样又有新的问题了:非对称量化多了这么些操作,有什么增益吗?
答:在激活函数是relu的时候,激活值全大于0,这个情况下还是用对称量化就会浪费一个bit的表示能力,只能[0, 127];
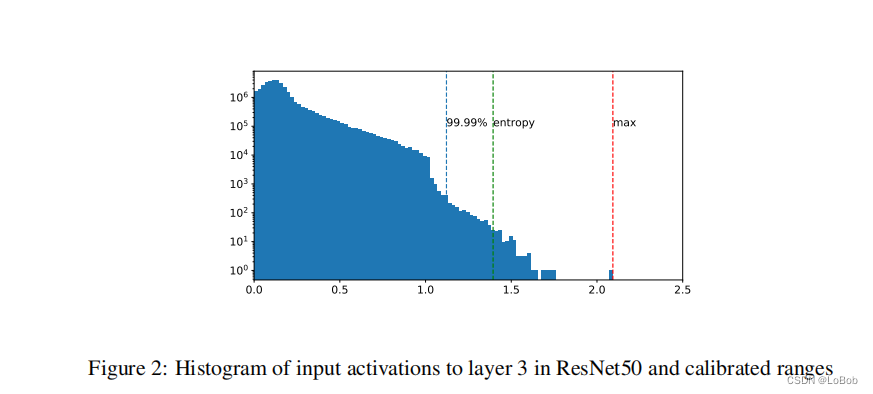
Calibration:Calibration是用来选模型参数和激活值的最大值和最小值,用来做截断。
又三种校准的策略:
max-min:tensor的最大值和最小值,这个策略没有截断。
KL散度(KL divergence):最小化量化后int8与float32数据的KL散度,tensorrt采用这个策略。
百分比(Percentile):选取tensor的99%或者其他百分比的数值,其余的截断。
4、PTQ:训练后量化¶
即对训练好的模型做量化,但不finetune。
前面发现per-tensor的量化,在有折叠BN的情况下会有比较大的精度损失,故作了table4的实验,可以发现在只量化weight的情况下,per-channel量化和max-min的校准策略,折叠BN并不会带来影响,证明了在这个策略下可以使用折叠BN。折叠BN的好处就是算子融合,把之前需要2层即conv+bn变成了1层,减少了计算和取值。
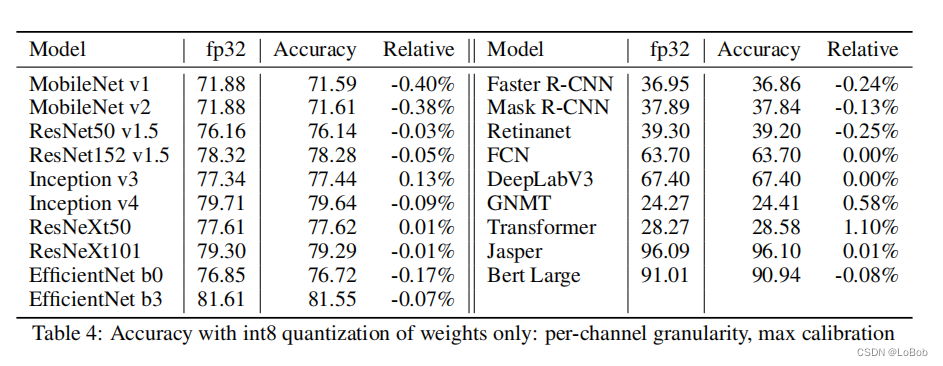
tabel 4仅仅只是weight量化那肯定是不够的,需要对activation也量化做的量化才是实际部署使用的,效果如下图table 5,可以看到不用的模型/任务(分类/检测/NLP),需要采用的校准策略是不一样的,也就是校准策略没有哪一中可以称霸。基本int8的量化,在分类、检测、NLP上精度损失都不大,是可以真实落地使用的量化比特位。
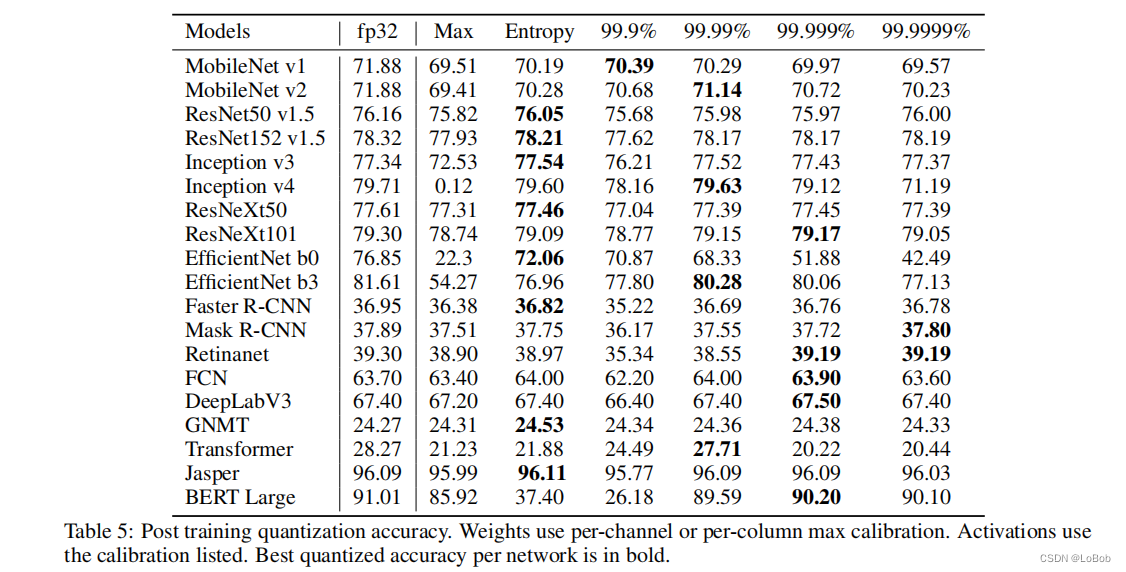
5、恢复精度的技术:Partial Quantization(部分量化)和QAT(量化中训练)¶
Partial Quantization:量化后对模型效果影响比较大(也就是更加敏感)的就用高比特来表示,用float32/float16/int16。这个敏感度判别采用最直接简单的方法:每次只量化一层跑一遍,看模型效果的影响,影响大的就更敏感,反之就不敏感。
因为前面的实验发现efficientNet精度影响比较大,用他来实验partial quantization
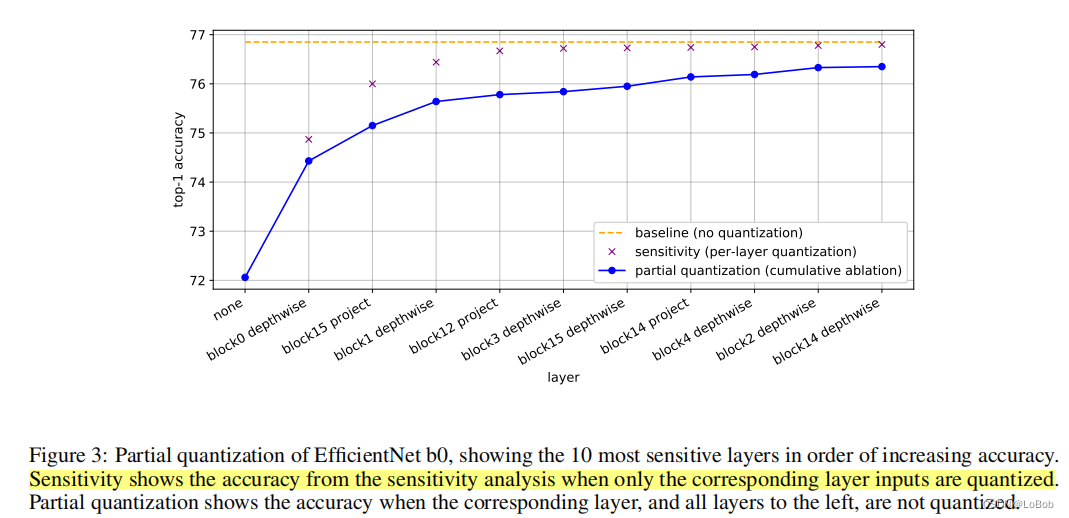
可以看出,最开始的层和最后的层对精度影响很大,另外depthwise conv对精度的影响也比较大。depthwise conv的问题可以使用weight equalization来缓解精度损失。
Quantization-Aware Training(QAT): QAT就是在训练中插入fake quantize节点 做dequantize(quantize(x, b, s), b, s),对quantize这个节点因为导数为0,采用STE(即梯度为0)来解决。QAT的实验如下table 7,会发现有些情况下QAT-int8比float32还好一丢丢,这时候论文作者的描述格局非常大:”Likewise, we do not interpret cases where accuracy is higher than fp32 as quantization acting as a regularizer, it is more likely to be noise or the result of the additional fifine-tuning.“,意思就是这只是实验中的“噪声”,也就是并不是方法多么sota,就只是实验的随机性罢了。大格局!
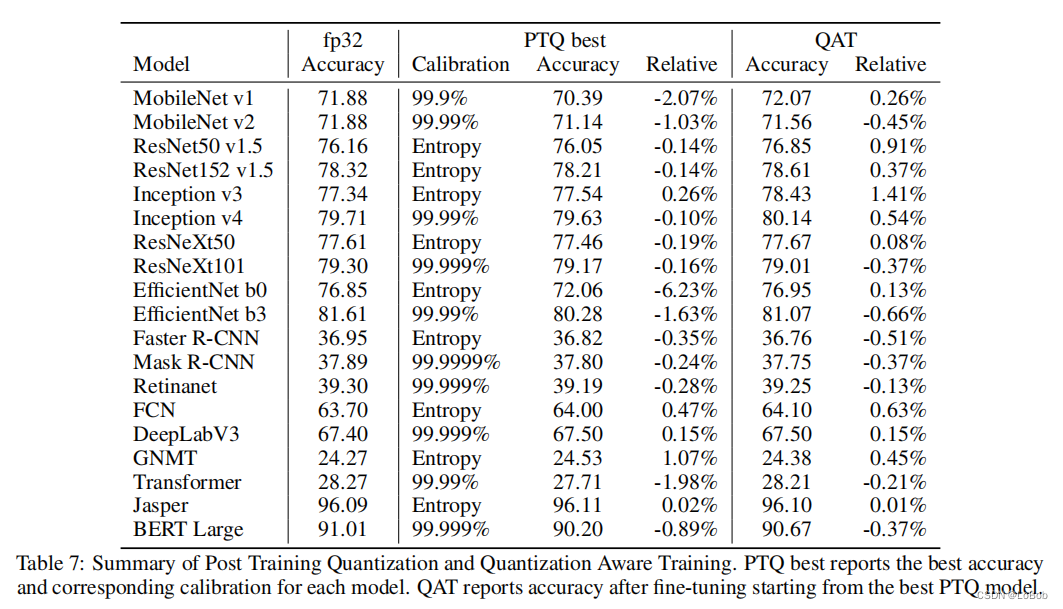
可学习的量化参数:作者实验了PACT的方法,学习截断值域。结论是:当预设的range合理的时候,PACT几乎没有增益,也就是告诉大家不用迷信这种方法。
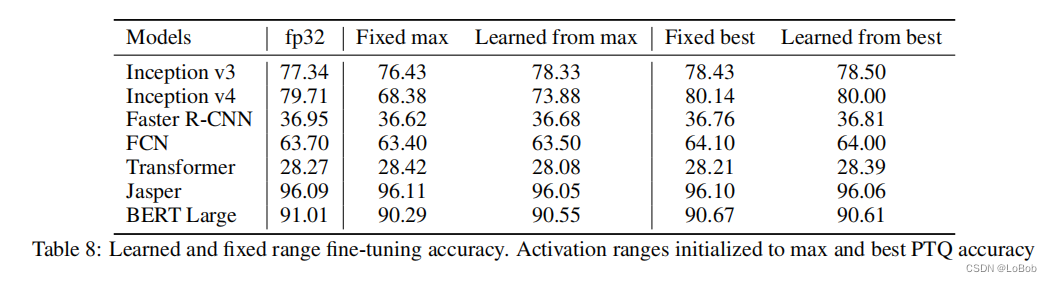
6. 推荐的量化的流程图¶
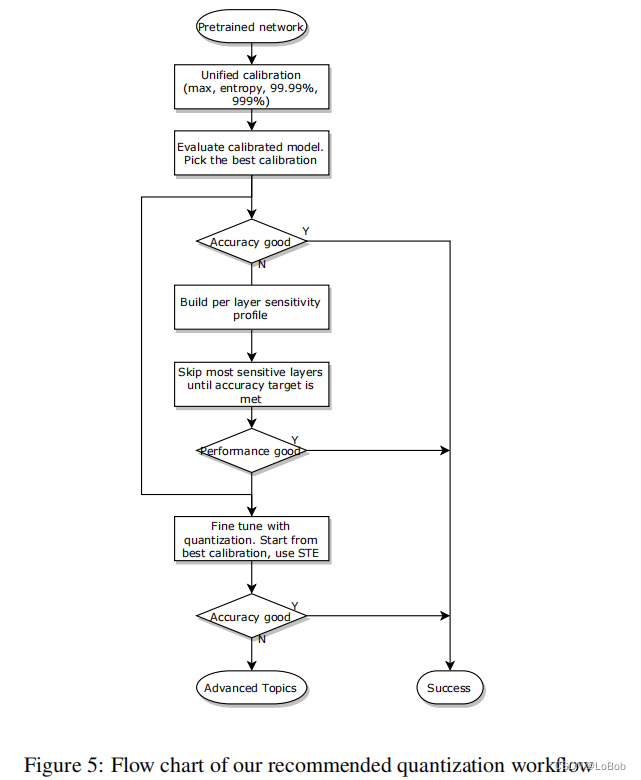
weight:对称量化+per-channel+max-min校准策略+[-127, 127] activation:per-tensor+对称量化
先进行PTQ,即可量化所有层,校准策略遍历完,max-min、KL散度、百分比99.99%/99.999%,达不到要求做部分量化;
Partial Quantization:只量化某一层跑推理,记录模型效果并且排序,用来选择敏感度,敏感度大的用高精度;,还是达不到要求用QAT;
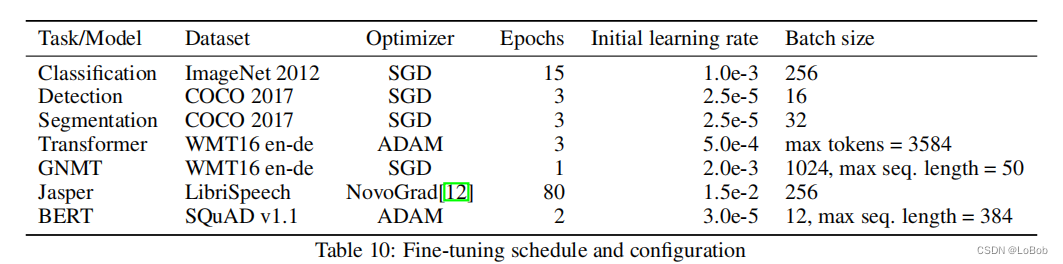
QAT:加载效果最好的量化模型参数,插入伪量化节点,用原来初始学习率的1%做完QAT的初始学习率,采用退化学习率衰减器。
论文附录有炼丹配方
本文总阅读量次