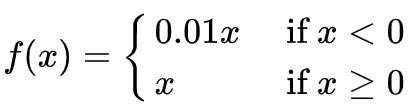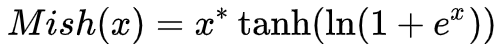工程部署(一)_ 移动端算子的选择_陈e
前言:本文首发于GiantPandaCV,未经允许请勿转载
此篇博客源于此前和朋友的讨论,在端侧部署、算力较为匮乏的板子上,普遍喜欢使用Relu和LeakyReLU激活函数,而我们常说的类似Sigmoid,Mish函数开销大指的是什么?这篇博客将从实验层面进行剖析,也是之前从零开始学CV之一激活函数篇:https://zhuanlan.zhihu.com/p/380237014的延伸。
以下仅代表个人观点,若有不当之处,欢迎批评指出。
一、激活函数¶
对于激活函数的详解,网上的资料实在是太多了,在我们日常工作中,经常见到的激活函数有relu, leakyrelu, sigmoid, swish, hardswish, selu, mish等等。举几个常见的,对于YOLO系列,YOLOv3使用的激活函数为LeakyReLU,YOLOv4则通过Mish函数提高模型性能,但带来的是高昂的开销,YOLOv5作者使用的是SiLU函数1,作为速度与精度的均衡。
可以说不同的激活函数带来的增益不尽相同,但并不是说开销越大,计算越昂贵的激活函数就一定最work,这里借一张v5s关于不同激活函数的消融图进行对比:
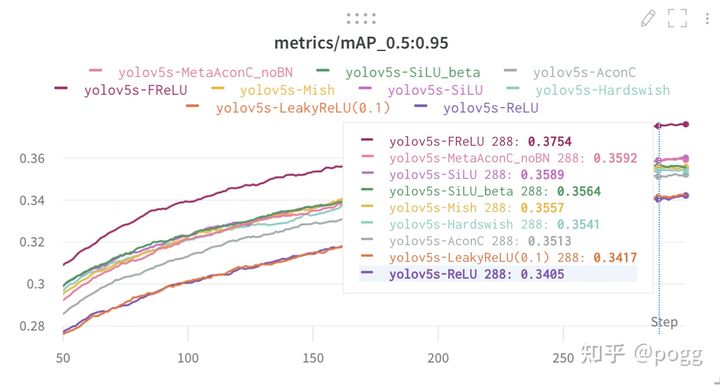
上图是在v5的issue中看到的一张作者对比不同激活函数的性能图,可以看到,虽然Mish函数的开销极大,但对于v5s这类小模型而言,带来的增益却并非最优,相比之下,swish函数复现的效果要超过Mish函数,同时,Swish函数也比Mish函数快了15-20%:
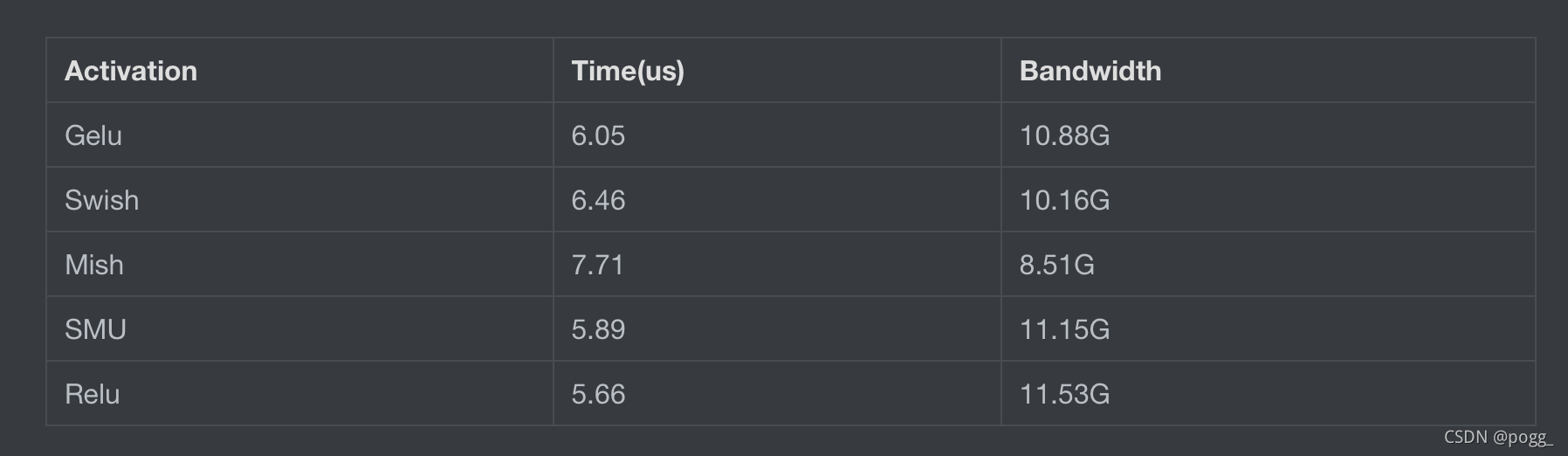
Test on Nvidia A100 - From oneflow zzk
上图为A100显卡上,不同激活函数的latency和Bandwidth的对比。
二、激活函数底层算子对比¶
但这篇博客更想对比的是模型部署时,不同算子的性能差异,我们通过调用ncnn向前推理框架的底层算子进行测试。
在对比前,为了保证Mat参数输入的随机性,我们采用仅含5个卷积层和3个池化层的模型对参数进行点乘运算,而后将这个输出结果送进激活函数算子进行运算:

static int init_net3x3(ncnn::Net* net, int* target_size)
{
net->opt.num_threads = 4;
//Test for multi thread
int ret = 0;
const char* net_param = "5xConv3x3x128.param";
const char* net_model = "5xConv3x3x128.bin";
*target_size = 224;
ret = net->load_param(net_param);
if (ret != 0)
{
return ret;
}
ret = net->load_model(net_model);
if (ret != 0)
{
return ret;
}
return 0;
}
static ncnn::Mat forward_net3x3(const cv::Mat& bgr, int target_size, ncnn::Net* net)
{
int img_w = bgr.cols;
int img_h = bgr.rows;
ncnn::Mat in = ncnn::Mat::from_pixels_resize(bgr.data, ncnn::Mat::PIXEL_BGR2RGB, bgr.cols, bgr.rows, target_size, target_size);
ncnn::Extractor ex = net->create_extractor();
ex.input("input.1", in);
ncnn::Mat out;
ex.extract("18", out);
return out;
}
static int ReLU(const ncnn::Mat& bottom_top_blob, const ncnn::Option& opt)
{
int w = bottom_top_blob.w;
int h = bottom_top_blob.h;
int channels = bottom_top_blob.c;
int size = w * h;
#pragma omp parallel for num_threads(opt.num_threads)
for (int q = 0; q < channels; q++)
{
ncnn::Mat ptr = bottom_top_blob.channel(q);
for (int i = 0; i < size; i++)
{
// fprintf(stderr, "Tensor value: %f ms \n", ptr.channel(q)[i]);
if (bottom_top_blob.channel(q)[i] < 0)
{
ptr.channel(q)[i] = 0;
}
}
}
return 0;
}
static int Swish(const ncnn::Mat& bottom_top_blob, const ncnn::Option& opt)
{
int w = bottom_top_blob.w;
int h = bottom_top_blob.h;
int channels = bottom_top_blob.c;
int size = w * h;
#pragma omp parallel for num_threads(opt.num_threads)
for (int q = 0; q < channels; q++)
{
ncnn::Mat ptr = bottom_top_blob.channel(q);
for (int i = 0; i < size; i++)
{
float x = ptr[i];
ptr[i] = static_cast<float>(x / (1.f + expf(-x)));
}
}
return 0;
}
/*
...The content is too long, omit the remaining 100 lines of code...
*/
int main(int argc, char** argv)
{
int target_size = 224;
ncnn::Net net3x3;
int ret = init_net3x3(&net3x3, &target_size);
cv::Mat m = cv::imread("C:/Users/chen/Desktop/3dd980d7f22fd0607c80f5ebc2c1c2e.jpg", 1);
ncnn::Mat out = forward_net3x3(m, target_size, &net3x3);
ncnn::Option opt;
opt.num_threads = 1;
int forward_times = 100000;
double tanh_start = GetTickCount();
for (int i = 0; i < forward_times; i++)
Tanh(out, opt);
double tanh_end = GetTickCount();
fprintf(stderr, "Forward %d times. Tanh cost time: %.5f ms \n", forward_times, (tanh_end - tanh_start));
/*
...The content is too long, omit the remaining 100 lines of code...
*/
return 0;
}
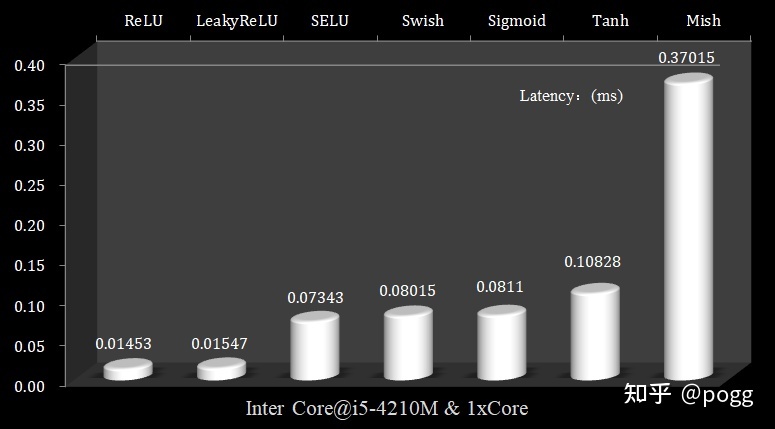
可以看出,ReLU和LeakyReLU的耗时最少,而Mish函数的耗时最久,且远远超过其他激活函数,以ReLU和LeakyReLU作为基准,我们可以看到这两个函数的复杂度为常数级别,即只进行加减乘除单一操作:
ReLU函数式:
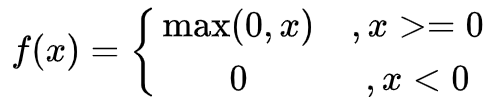
两个算子的图像:
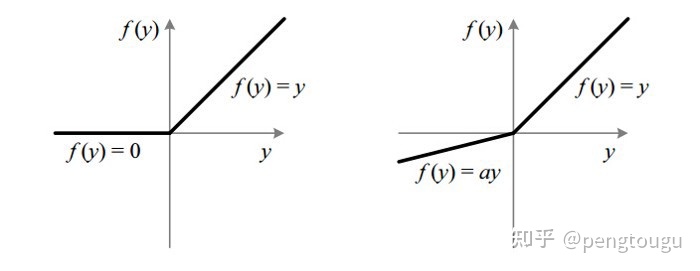
左图为ReLU,右图为LeakyReLU.
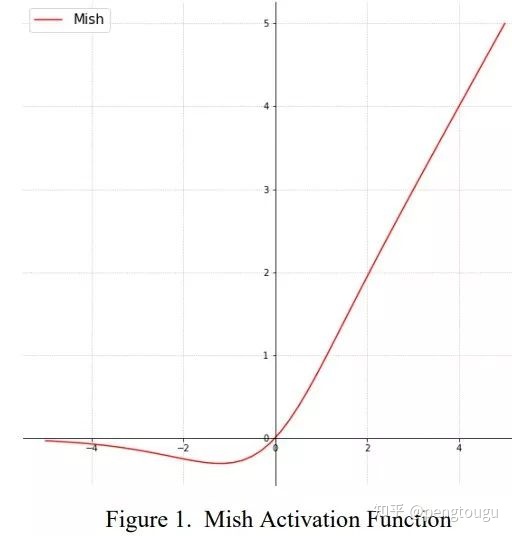
Mish函数式:
函数图像:
不仅如此,我们将参数量扩大为原来的4倍(331024),进行10万次forward,得出每次推理Latency:
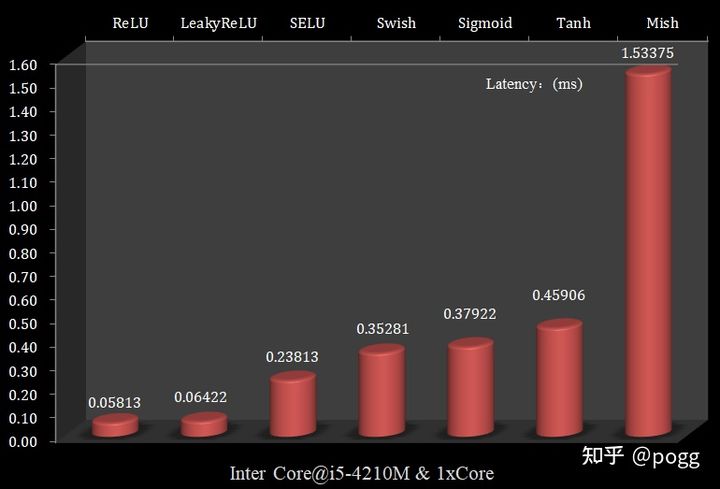
可以看到,当参数量增多,指数量级激活函数与常数量级激活函数的延迟比会越来越大,在参数量为33128时,
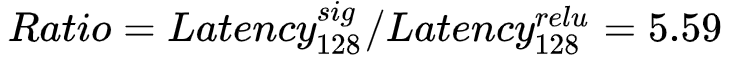
而参数量翻到4倍时:
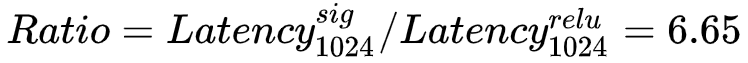
当输入参数量增多时,单次向前推理浮点运算增加,函数所占用的内存增多,而带来的直接影响是板子超频功能不稳定,可能玩过板子的朋友们知道,内存频率直接影响了计算平台的带宽,而函数/模型的运行效率受限于板子或计算平台的带宽资源,这也可能是指数运算操作在输入参数大幅增加后运行效率略受影响的原因。
下图为不同激活函数运算时所占用内存大小:
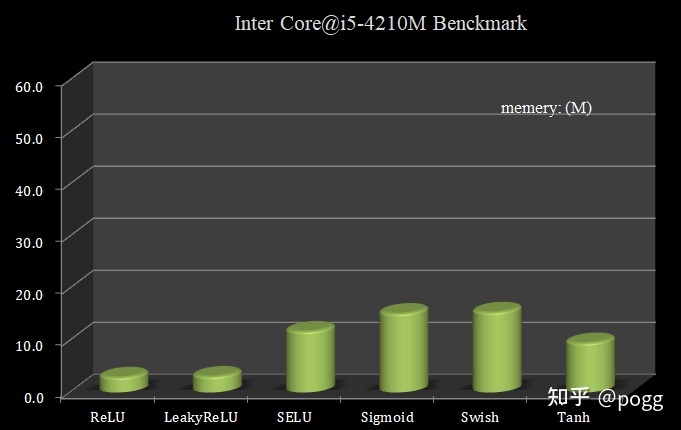
对于ReLU和LeakyReLU等激活函数,是我们在轻量级网络和移动端部署最常见的(目前还没见过带Mish函数的轻量级网络),一方面,作为常数量级算子,耗时延迟低,计算快;另一方面,不涉及指数操作等大量复杂运算指令,算子对于处理参数暴涨的情况,也能从容应对,对于算力资源极度匮乏的板子来说非常合适。
本文总阅读量次