F8Net只有8比特乘法的神经网络量化

F8Net:只有8比特乘法的神经网络量化¶

【GaintPandaCV导语】

F8Net用定点化量化方法对DNN进行量化，在模型推理只有8-bit的乘法，没有16-bit/32-bit的乘法，采用非学习的方法即标准差来定小数位宽。目前是我看到的第一篇硬件层面全8-bit乘法的模型推理的方法。

论文出处：ICLR2022 Oral《F8Net: Fixed-Point 8-bit Only Multiplication for Network Quantization》

问题1：什么是定点化(fixed-point)?¶

答曰：这个链接讲的非常好浮点数的定点化 - 知乎 (zhihu.com) ，我复述(抄一下)一下：

1.定点转换¶

以两个16位的浮点数相乘为例
2.918 × 3.1415926 = 9.1671672068
将此浮点数定点化，定点要求为Qn=12（这里Qn=12表示小数位数占12bit），取符号位为1bit，则整数部分为3bit。
2.918 × 2^12 = 11952.168  定点化后取整为： 11952;
3.1415926× 2^12 = 12867.8632896 定点化后取整为： 12868;
以上做舍入误差后取整数。

2.定点数相乘：¶

11952 * 12868 = 153798336.

3.定点数还原为小数¶

153798336 / (2^24) = 9.167095184326171875
两个12bit的数相乘，结果为24bit，因此除以2^24可以还原原数据，由于存在舍入误差

还有2个小点“量化误差与量化精度”和“无损定点化”，请大家去链接上面看，记得得作者点赞！！！

问题2：为什么要做这样的量化，跟之前的量化有什么不同？¶

请看图，因为目前“常识”中的量化推理有int32的乘法，IAQ(也就是tflite的量化推理)把scale用定点化来逼近，需要int16或者int32的乘法，也就是说现有的量化推理还是需要int32的乘法，F8Net想做的事情就是在量化推理中只有int8的乘法，没有16bit/32bit的乘法。

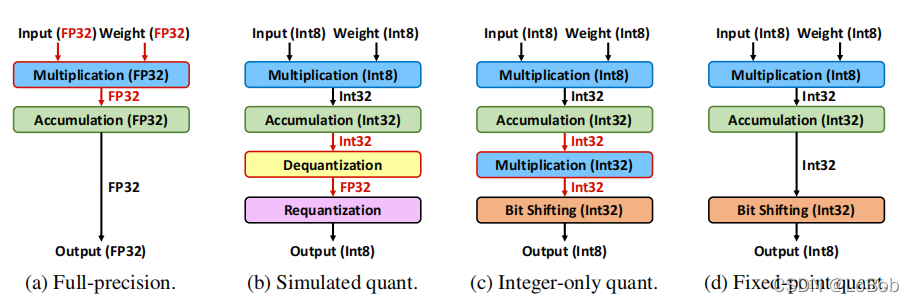
首先来总结一下，F8Net做了什么事情：

1、模型量化推理只有8-bit位宽的乘法；
2、提出一个选择小数位宽的方法，对weight和activation都做定点化；
3、采用PACT的方法优化定点化的参数，把定点化和PACT的方法结合，推导出这样的优化公式；
4、定点化有效权重和有效偏差，有效权重和有效偏差指的是fold bn的con-bn的参数；
5、对残差块的d定点化参数对齐方法的实验和探究；
6、高精度的乘法对神经网络的性能来说，不是必须的。

如何选择小数位宽：用标准差来选择小数位宽¶

看到这里的大家肯定有疑问，“就这？？？这论文是水文啊？？用标准差来选择位宽，这个太naive吧。” emmm，别急，好好看他怎么做的。

首先，作者用高斯分布(这里有个小问题，为什么用高斯呢)生成一堆随机数。采用均值为0，不同的方差来生成随机数，然后用不同的小数位宽来做定点化，计算他的相对量化误差。

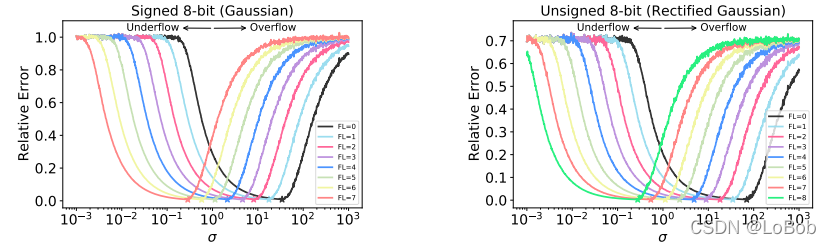
看这个图，横坐标是不同数值的标准差，纵坐标是相对量化误差。可以发现不同的FL(小数位宽)，都有自己相对误差最小时候的标准差，也就是说，可以根据标准来选择小数位宽。

那么这里就会有质疑：这是因为你用了假设，这个假设是高斯分布。这个读者可以思考一下，这种假设是否合理。我的观点是：合理！

ok，那么找到了一个选位宽的标准了，接下来呢，这个数值怎么计算呢？看另外一张图。

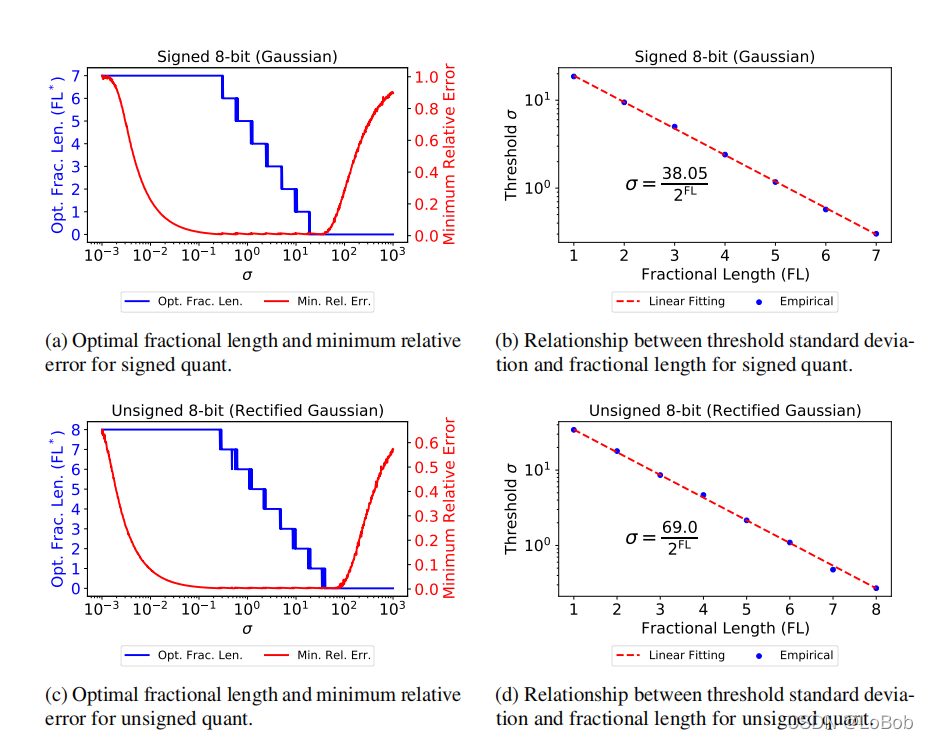
把图2转换成图3(a)和©，这个转换非常好理解，就不描述了。然后找蓝色线的阶梯和红色线的关系，找到每个阶梯对应标准差的阈值。作者把他取log后，发现这个阈值与位宽是接近线性的，那么得出图3(b)和(d)的阈值经验公式。那么小数位宽的选择阈值已经找到了。这个F8Net的最主体的部分已经完成了。

这里大家又有疑问了：为什么要用取log？这就是传说中的调参吗？

分享一下我的理解：看图3(a)和©阶梯对应的红色线，这个尺度下，你只能看出随着阶梯下降，红色线有一点点上升的趋势。这个尺度下你看不清楚，要怎么办？换个尺度，而log就是非常常用的方法。

与PACT方法结合：找截断阈值¶

这里先抛出问题：为什么要用PACT？做量化不外乎：什么量化方法(线性量化/非线性，对称量化/非对称量化等等)，以及这么找数值阈值(也就是截断阈值)。PACT就是非常简单又非常使用的方法。我在做量化训练的时候也是用了PACT。PACT YYDS！

这里公式非常好理解，也非常好推导，也就是简单的变换而已，这里就不做公式推导，因为推导非常简单。

有效权重weight与有效偏差bias¶

什么是有效weight和有效bias？这里说的是conv和bn融合后的conv_bn的weight和bias。

既然是对融合后的conv_bn做定点化，那么这个就有QAT一直有的一个细节，这个BN的参数这个更新或者怎么算。因为通常是先做conv，后面再做bn；也就是说fold bn的时候conv层需要的gamma和beta还没有算，那么怎么办呢？MQBench对QAT的fold BN的几种方法做了很详细的分析，大体有forward一次和forward两次这两种方法，Pytorch和MQBench采用了forward一次，F8Net采用了forward两次。第一次forward是用来更新bn的参数，第二次forward是用来定点化和更新参数。

Fix scalling factor定义为:

对于两个连接层的activation，定点化activation公式（也就是conv_bn的输出，也就是y=wx+b）如下：

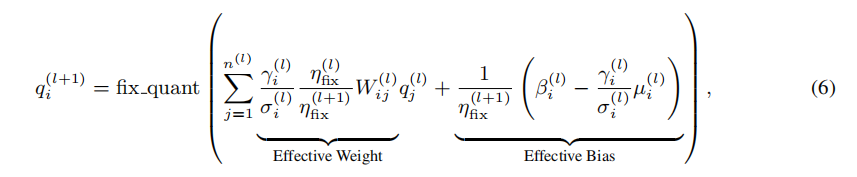
公式中，α是全精度的可训练浮点数，所以Fix scaling factor也是全精度的。所以这个全精度的α要消除or融入到其他操作，不然就不是全int8的乘法模型推理了。F8Net选择融入有效权重中。γ， β，σ，μ都是BN层的参数，这个BN的参数更新用两次forward。

对于输入的小数位宽采用缓存更新，动量设置为0.1，也就是最新的值要乘以0.1，这个操作更BN层参数是一样，但bn层是最新的值要乘以0.9。

残差层的Fix scalling Factor¶

看公式(6)，$\eta_{\text {fix }}^{(l+1)}$我们在当前层的时候是不知道的，因为在下一层才能算出来，所以这里作者用存在buffer中的小数位宽来计算$\eta_{\text {fix }}^{(l+1)}$。

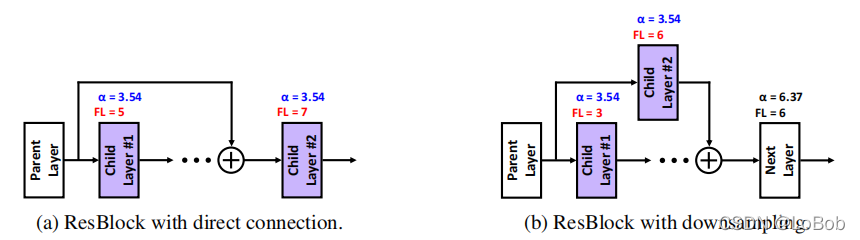
那么看上图的残差模块，对于残差，父层有多个子层，那么这个$\eta_{\text {fix }}^{(l+1)}$要选择哪一个子层(也就是哪个小数位宽)来计算呢父层的有效weight呢？ - 答曰：用主子层，就是直接连接的。

子层的小数位宽呢，要统一还是各种不一样呢？实验得出，如果小数位宽一样，精度损失比较大；子层有各自的小数位宽，精度就与全精度的接近。这里作者的解释是：小数位宽有两个作用，一个是计算fix scaling factor，一个是表征值域（截断值域），那么各自子层有自己的小数位宽相当于有各自的截断值域。

总结一下：对于父层后面有多个子层的网络结构，父层和子层共享截断阈值α；计算父层的有效weight和bias用主子层的小数位宽；计算各个子层的有效weight和bias的时候，使用各自的小数位宽。

OK，全文的方法都介绍完了。

实验情况¶

1、传统的QAT：先训练一个全精度的模型；再加载这个pre-trained的模型参数，用完全相同的超参数来重新训练；使用F8Net的方法来选择小数位宽。

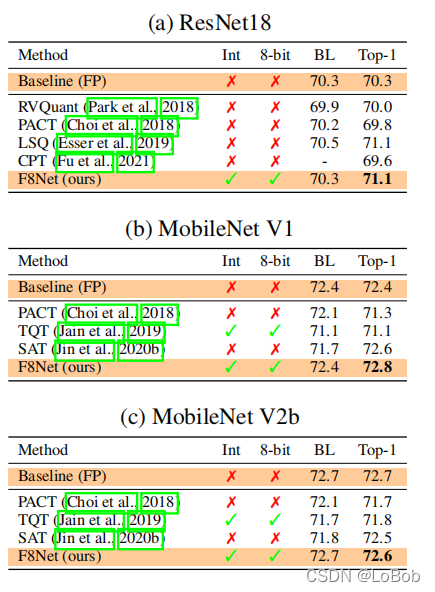
2、Tiny fine-tuning的方法，来自于HAWQ_V3：加载一个pre-trained，保持很小的学习率(1e-4)，用

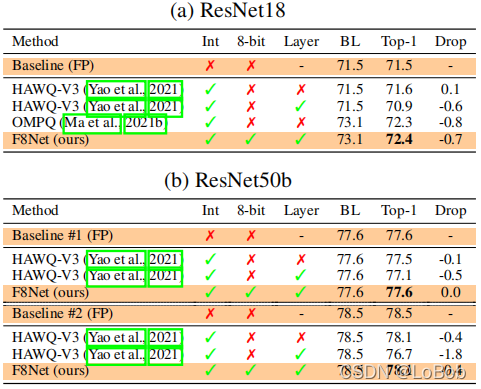
128个数据训练500个iteration；使用网格搜索确定小数位宽。 在MobileNet的量化效果非常不错，基本可以达到无损量化。

采用F8Net训练好后的小数小数位宽的情况：

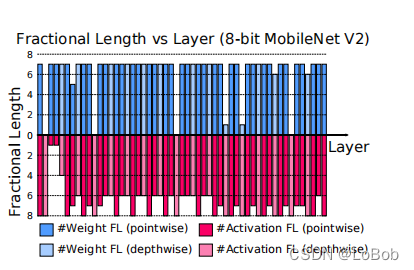
可以发现对于weight来说，pointwise的conv小数位宽基本都比较大，而depthwise的小数位宽有比较小的。

总结¶

F8Net首先是用IEEE 754标准定点化成8bit，用标准差来选择weight和activation的小数位宽，用PACT的方式来找截断阈值，把PACT的浮点类型的截断阈值融入有效weight和有效bias， 用有效weight和有效bias，对齐不同层的量化参数(这里指的是小数位宽和截断阈值)。个人觉得是个很优秀的工作，虽然一开始用标准差来定小数位宽，这第一眼看很简单，但认真一看，当中有很多细节需要解决。

有效weight和有效bias这个方式其实就是fold BN，forward两次解决QAT参数更新是已有的方法，多个子层的量化参数对齐问题，是工程上非常重要的问题。

Btw：看了openreview的“讨论”，我觉得这边工作还是很solid的。

F8Net: Fixed-Point 8-bit Only Multiplication for Network Quantization | OpenReview