EWSG 基于元素级梯度缩放_LoBob

EWGS：基于(element-wise)元素级梯度缩放的网络量化

论文出处：《NetworkQuantizationwithElement-wiseGradientScaling》时间：2021CVPR 单位：YonseiUniversity

0. 前言¶

做量化训练的时候，要加入量化节点，即dequantize(quantize(x,b,s),b,s)，那么在后向传播的时候发现这个quantize的操作导数处处为0，那么直接不管的话，梯度在quantize的round这个op之后就为0了，就没法训练下去了。2013年的时候，Bengio用straight-throughestimator(STE，直通估计)来解决quantize导数为0的问题，其实就是bypass。直接就忽略quantize这个操作的误差了，得到的梯度也是mismatch的，必然是次优的解决办法。STE存在问题有大佬已经写过了，可以看看这个连接，我就不copy-pasty了，量化训练之补偿STE：DSQ和QuantNoise-知乎(zhihu.com)。那怎么修改STE的问题呢？一个最简单的想法就是，找一个可导的quantize，这个idea在2017-2019有部分论文在做块工作，比如HWGQ、Lq-Net、DSQ等。2020后做可导quantize的工作没怎么关注了，因为不好落地，对speedup有影响。这篇工作EWGS的思路和方法很简单，很符合直觉，个人觉得是值得阅读的文章。

1、EWGS公式¶

一句话说EWGS：给出离散值(也就是量化值)的梯度，EWGS会根据量化误差来自适应缩放梯度，让做梯度更新的时候方向和模值更加准确。

总结EWSG的工作：

1、考虑了quantize输入和输出的误差，自适应的放大或者缩小梯度

2、将比例因子与任务损失二阶导数联系起来，使用Hessian矩阵的迹来估计因子

3、不需要广泛的超参数搜索。

l和u是一组fp32数的最大值和最小值，下面的公式就是把输入x映射到0，1的浮点数值

$x_{n}=\operatorname{clip}\left(\frac{x-l}{u-l},0,1\right)(1)$

把上一步归一化后的数值乘上int数值可以表征的大小，就做完了从fp32到in8的量化，round的操作是取整，分子是做fp32->int8，分布是把int8转回去fp32，因为这是做量化训练。这x_n和x_q是有误差的，来源于round这个操作。

$x_{q}=\frac{\operatorname{round}\left(\left(2^{b}-1\right)x_{n}\right)}{2^{b}-1}(2)$

之后就可以输入量化后的输出了Q_w和Q_a,Q_a因为经过了Relu后是非负数，那么就直接用x_q表示；而Q_w是对称量化，有负数的，那么先-0.5就把x_q的移到了[-0.50.5]，乘以2就表示正确了。

$Q_{W}(x)=2\left(x_{q}-0.5\right),Q_{A}(x)=x_{q}(3)$

这里有一个很重要的细节，就是对量化后卷积层/全连接层的输出加了一个α缩放因子，这一点trick。

这个公式就是EWSG的公式了

$g_{x_{n}}=g_{x_{q}}\left(1+\delta\operatorname{sign}\left(g_{x_{q}}\right)\left(x_{n}-x_{q}\right)\right)(4)$

STE是这样的， $\mathcal{G}_{\mathbf{x}_{n}}=\mathcal{G}_{\mathbf{x}_{q}}$ , 直接将导数为0或者不可导的变成了1，直接直通。因为这些下标太难打了，我直接截图了。一个是公式(1)的梯度，一个是公式(2)的梯度。δ是大于0的数值，当δ等于0的时候，EWSG就是STE了。

STE是次优的原因：

（1）多个 $x_n$ 可以产生相同的 $x_q$ ，大白话就是多个fp32的数值变成同一个int值；

（2） $x_n$ 提供的相同梯度对每个 $x_q$ 都有不同的影响，大白话就是虽然梯度 $x_n$ 的一样的，但是对应的 $x_q$ 是不一样的，这个就是mismatch的问题。

2、如何确定δ数值，基于海森矩阵的方法¶

这边就是公式推导了。

将EWSG公式(即可公式4)展开，凑成有导数的形式，x_n-x_q就是量化误差了，也就是符号ℇ

$\begin{aligned} g_{x_{n}}&=g_{x_{q}}+\frac{g_{x_{n}}-g_{x_{q}}}{x_{n}-x_{q}}\left(x_{n}-x_{q}\right)\\ &=g_{x_{q}}+\frac{g_{x_{q}+\epsilon}-g_{x_{q}}}{\epsilon}\left(x_{n}-x_{q}\right)\\ \end{aligned}\\$

$g_{x_{n}}\approx g_{x_{q}}+g_{x_{q}}^{\prime}\left(x_{n}-x_{q}\right)$

$g_{x_{n}}\approx g_{x_{q}}\left(1+\frac{g_{x_{q}}^{\prime}}{\left|g_{x_{q}}\right|}\operatorname{sign}\left(g_{x_{q}}\right)\left(x_{n}-x_{q}\right)\right) g_{x_{q}}^{\prime}=\frac{\partial g_{x_{q}}}{\partial x_{q}}$

其中，这项就是导数的导数也就是二阶信息，也是常说的海森信息

$g_{x_{q}}^{\prime}=\frac{\partial g_{x_{q}}}{\partial x_{q}}$

所以，δ的数值就确定了

$\delta=\frac{g_{x_{q}}^{\prime}}{\left|g_{x_{q}}\right|}$

海森矩阵的公式推导基于了一个假设(没怎么看懂，也不想深入探究，摆烂)，得出这么个公式，

$\mathbb{E}\left[\mathbf{v} \mathbf{v}^{T}\right]=I$

代入并且进行变换，

$\begin{aligned} \operatorname{Tr}(H) &=\operatorname{Tr}(H I)=\operatorname{Tr}\left(H \mathbb{E}\left[\mathbf{v}^{T}\right]\right) \\ &=\mathbb{E}\left[\operatorname{Tr}\left(H \mathbf{v} \mathbf{v}^{T}\right)\right]=\mathbb{E}\left[\mathbf{v}^{T} H \mathbf{v}\right] \end{aligned}$

最后δ的公式如下：N是海森矩阵中对角线元素的个数，G是由梯度Gx的分布决定的梯度表示。

但这个变换对于计算的意义我还是没看懂，因为这样还是要计算海森矩阵，估计也是用pyHessian的library算的，是用其他近似的方法求个海森矩阵，具体在HAWQ(v1、v2、v3)（下次一定写这三篇工作）。

个人觉得这个变换很凑数，也可能自己没看看懂那个假设，有看懂的大佬麻烦指正我！。

$\delta=\frac{\operatorname{Tr}(H) / N}{G} (5)$

实验中发现梯度很多是0，这样梯度的平均值偏向于0，把G设置成偏大的数：

$3 \sigma\left(\mathcal{G}_{\mathbf{x}_{q}}\right)$

3、实验¶

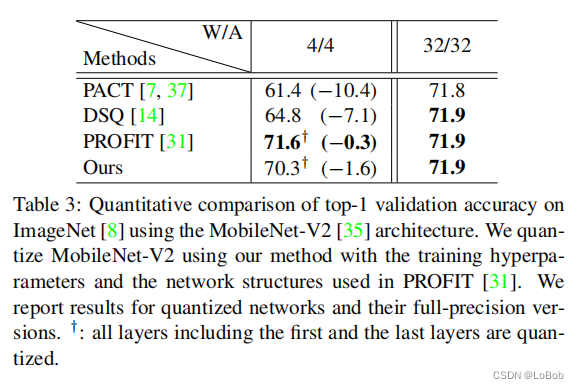
实验我就不贴ResNet的效果了，因为大差不差，直接STE+trick也能有差不多的性能，直接看mobilenet的实验，是比PROFIT(ECCV2020)的差，打不过啊。但EWGS的好处在于简单，且推理的时候并没有增加其他操作，戏虐说辞"无痛涨点"。其他的实验图意义不大，就不看了。

4、总结¶

EWGS结果没有超过前人的工作，我比较欣赏的是他的方法很简单，而且不给推理增加负担，是篇好工作。CVPR2020也有一篇做量化训练的时候修改梯度的，UnifiedINT8，通过修改梯度的方向和数值来缓解mismatch带来的影响。但EWGS从数学上个人觉得更加可解释和合理。故记录一下。

本文总阅读量次