ICML2022——Out-of-Distribution Detection with Deep Nearest Neighbors¶

0. 论文信息¶

标题：Out-of-Distribution Detection with Deep Nearest Neighbors

作者：Yiyou Sun, Yifei Ming, Xiaojin Zhu, Yixuan Li (University of Wisconsin - Madison)

原文链接：https://arxiv.org/pdf/2204.06507.pdf

代码链接：https://github.com/deeplearning-wisc/knn-ood

1. 介绍¶

由于经典的机器学习方法通常假设模型训练和测试的数据是独立同分布的(IID, Independent Identical Distribution)，这里训练和测试的数据都可以说是 In Distribution(ID)。在实际应用当中，模型部署上线后得到的数据往往不能被完全控制的，会出先一些样本外的数据，也就是说模型接收的数据有可能是 Out-of-Distribution (OOD) 样本，也可以叫异常样本(outlier) 指的是模型能够检测出 OOD 样本，而 OOD 样本是相对于 ID 样本来说的。如今的深度模型常常会对一个 OOD 样本认为是ID样本中的某一个类，并给出高的置信度，这显然是不合理的。举个通俗的例子，我们利用一个包含“猫”和“狗”两类的数据集训练一个二分类器。如果测试的时候，出现了“人”的样本，如果利用传统的softmax对输出的logit进行处理，那么我们会认为该样本属于“猫”或“狗”的一类，这显然对模型的部署是有影响的，所以我们希望我们的模型能够不把它判定为“猫”或者“狗”，而是判定它为OOD。如何让模型识别出 OOD 样本对 AI 的发展有很重要的意义，特别是 AI 安全。

最近出现了一系列丰富的 OOD 检测算法，其中基于距离的方法 (distance-based methods) 显示出非常卓越的性能。 基于距离的方法(Lee et al., 2018 ; Tack et al., 2020; Sehwag et al., 2021) 利用从模型中提取的特征嵌入(feature embedding)，并假设：在测试中OOD的样本相对训练中的ID样本相对来讲更远。但这些方法都把feature embedding的空间空间分布建模为多变量的混合高斯分布 (mixture of multivariate Gaussian distributions GMM)，这显然是作用有限的，因为很显然视觉信息非常复杂，不是用一个很简单的GMM就能描述的，所以可能这种方式叶比较受阻。其实利用参数相关的分布假设来描述真实世界中的各种分布显然是非常有挑战的。马毅老师也在表达过高维空间特征的复杂性。

所以本文提出了一个问题：

Can we leverage the non-parametric nearest neighbor approach for OOD detection?

我们可以利用非参数最近邻方法进行 OOD 检测吗？既然基于参数估计的分布假设可能不work，那我们能不能基于一些很简单的非参数方式来解决OOD问题？来自University of Wisconsin - Madison的团队设计了一种非常简洁的方式，给出了肯定的回答。

为了检测 OOD 样本，我们计算第 k 个嵌入之间的最近邻 (KNN) 距离测试输入和训练集的嵌入和使用基于阈值的标准，用于确定输入是否为 OOD与否。 简而言之，提出的方法进行非参数的估计，基于深度k-NN distance将数据分成两组（ID vs. OOD）。

方法具有以下几个优点：

• 无分布假设：非参数最近邻方法不对底层特征空间施加分布假设。因此，KNN 提供了更强的灵活性和通用性，即使在特征空间 不符合高斯混合。-

• 不依赖OOD数据：测试过程不依赖未知数据的信息。距离阈值仅根据 ID 数据进行估计。

• 易于使用：近似最近邻搜索的现代实现允许我们在几毫秒内完成此操作，即使数据库包含数十亿张图像（Johnson 等人，2019 年）。相比之下，马氏距离需要计算协方差矩阵的逆矩阵，这在数值上可能是不稳定的。

• 模型无关：测试过程适用于各种模型架构，包括 CNN 和最近的基于 Transformer 的 ViT 模型。

此外，该工作说明了 KNN 也与训练过程无关，并且与在不同损失函数下训练的模型兼容（cross-entropy loss和contrastive loss）。但可以看到基于对比学习的方式，由于特征聚合的更加紧凑，显然依照k-NN的性能也更优。

2. 方法¶

方法也非常简单：就是直接根据正常的训练模式（用交叉熵或者对比学习的损失函数都可以，单纯训练一个分类模型）一个模型编码器 $\phi$ 来编码得到训练集的特征 $\mathbb{Z}_{n}=\left(\mathbf{z}_{1}, \mathbf{z}_{2}, \ldots, \mathbf{z}_{n}\right)$，把这些特征作为ID的特征，来基于距离来判断测试样本是否为OOD。然后就是测试阶段，用同样的编码器来提取该样本的特征，经过正则化后（除以normalization），计算与$\mathbb{Z}_{n}=\left(\mathbf{z}_{1}, \mathbf{z}_{2}, \ldots, \mathbf{z}_{n}\right)$的距离，并按照距离大小进行增大排序，即得到$\mathbb{Z}_{n}^{\prime}=\left(\mathbf{z}_{(1)}, \mathbf{z}_{(2)}, \ldots, \mathbf{z}_{(n)}\right)$ ，直接把与第k小的距离作为输出的score，依照该score找到一个阈值来判断是不是OOD，这个阈值 $\lambda$ 自然要根据召回率和查全率的平衡来选择。

3. 实验¶

值得一提的是， 工作使用 Faiss ，FAIR设计的一个用于高效最近邻搜索的库。具体来说，该份工作使用 faiss.IndexFlatL2 作为欧式距离的索引方法。 在实践中，我们预先计算所有图像的嵌入并将它们存储在一个键值映射，使 KNN 搜索高效。 ID数据的嵌入向量只需要在之后提取一次训练完成。

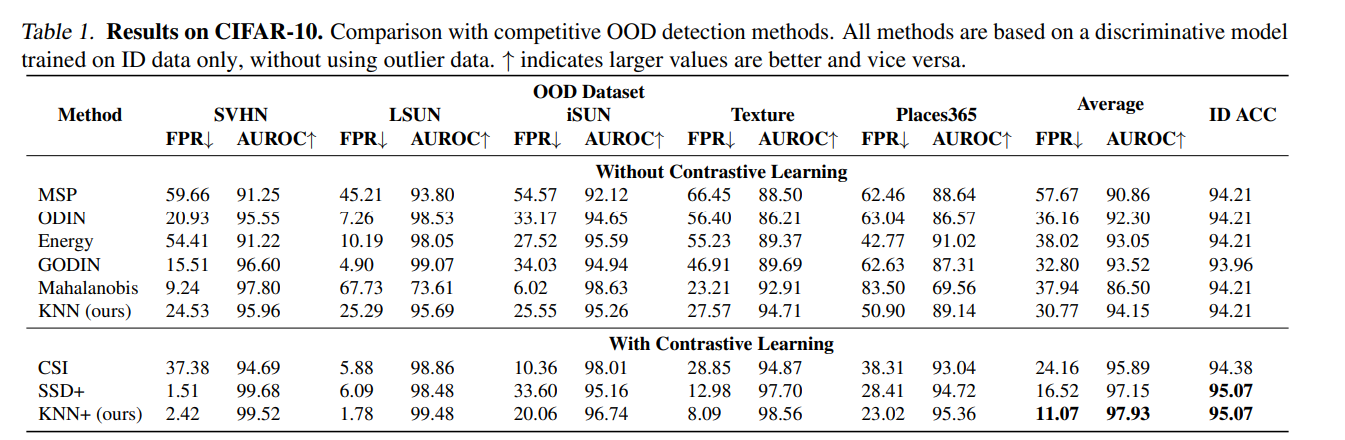
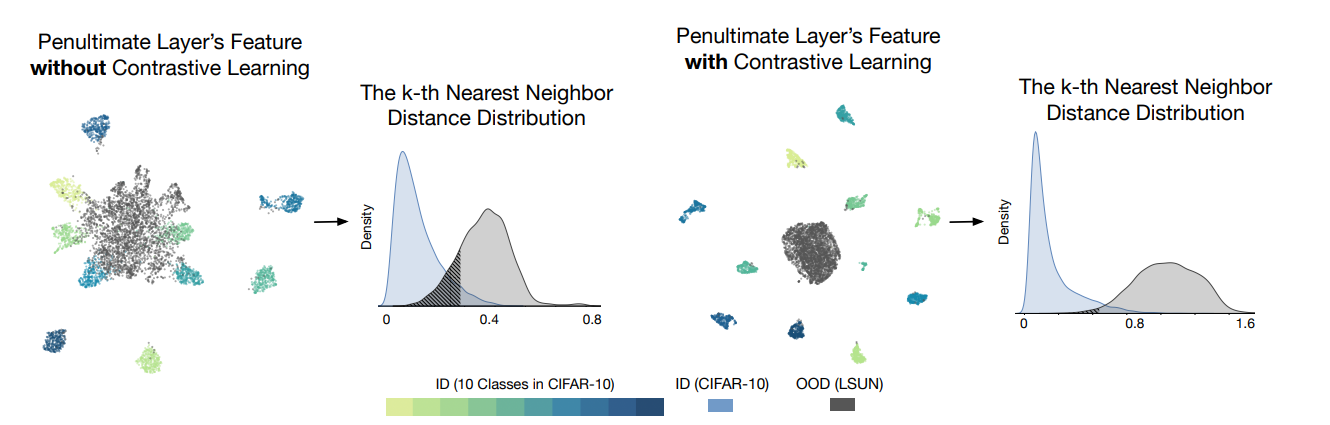
首先可以看到，这种不需要训练、不需要收集任何OOD数据的模型，在CIFAR-10上超过了采用特定的有参分布来描述ID数据的方法。正如上图可视化也可以发现，基于对比学习的方式能很好的对ID数据进行聚合（拉近正样本之间的距离，拉开负样本之间的距离），所以其性能显而易见的要高于不采用对比学习的方式。

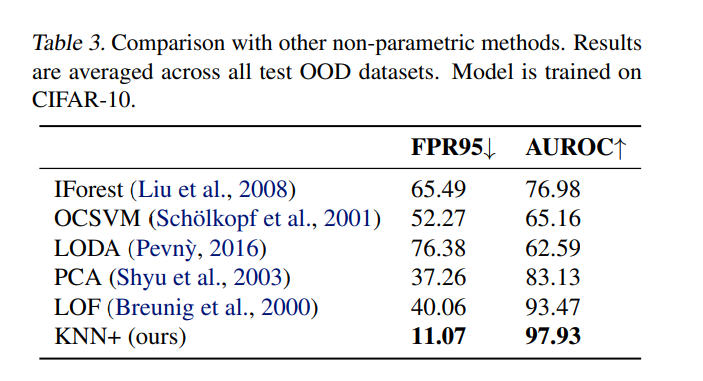
在CIFAR-10上这种简单的方法也显著好于其他无参估计的方法。

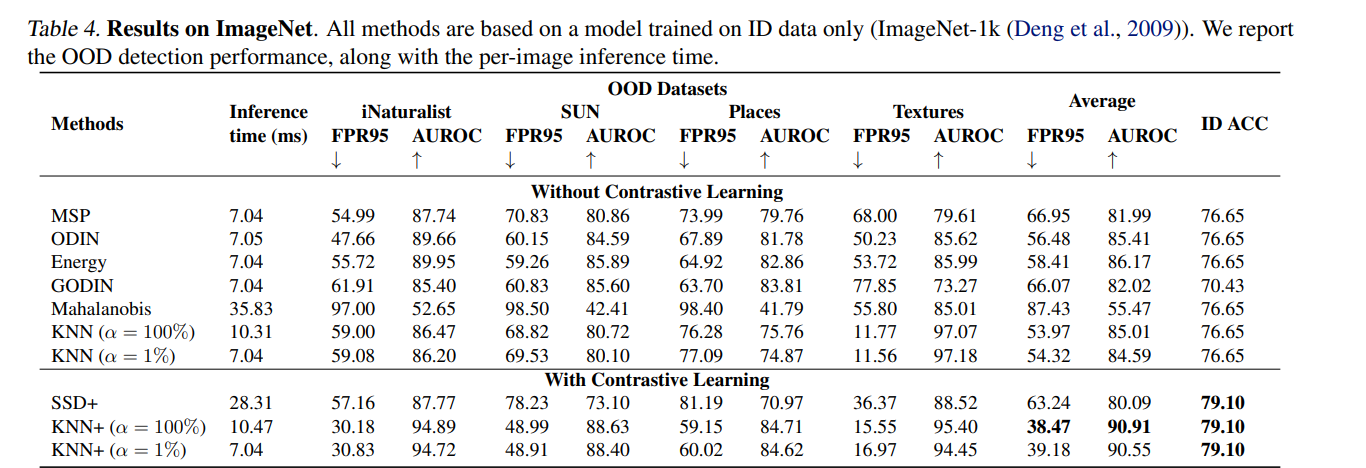
偏ML的论文经常会被诟病泛化性不足，只能在一些小数据集上进行实验，而到更大规模的数据集上就歇菜了。但该方法上升到更scale up的数据集，如ImageNet上，仍然可以表现地非常好。

其中的$\alpha$表示在类似ImageNet大数据集只随机采用一定比例的训练集来进行计算，从而减少noise对分类的影响。论文也对关键性的超参数进行了分析。由于该方法只是测试阶段采用，训练阶段没有任何不一样的地方。

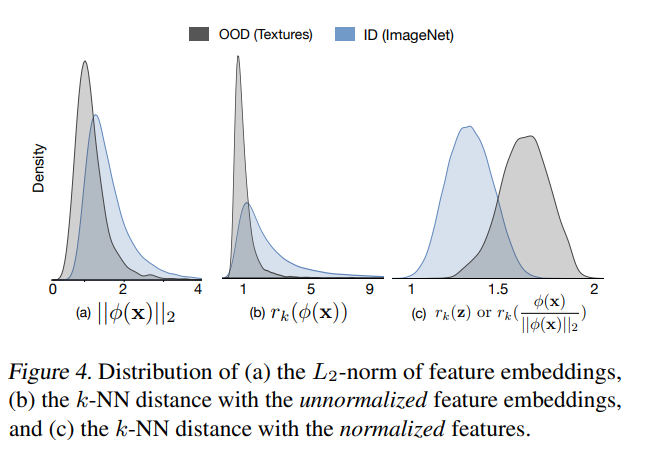
另外对于为何要对OOD数据进行正则化，论文也做出了分析：因为测试集和训练集提取出的特征模长显著不一样，但距离跟模长又非常相关，所以进行正则化可以避免不同集合模长不同对于检测效果的影响。

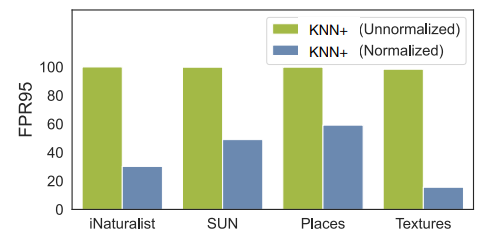
可以观察到，采用正则化的vector也可以非常显著的提升模型性能。

4. 理论阐释¶

论文展示了这种基于 KNN 的 OOD 检测器可以拒绝与估计的贝叶斯二进制等效的输入决策功能，从而完成OOD的检测。 一个小的 KNN 距离$r_{k}(z_{i})$直接转化为 ID 的概率很高，反之亦然。具体推导如下：

With the setup specified above, if $\hat{p}_{\text {out }}\left(\mathbf{z}_{i}\right)=\hat{c}_{0} 1\left\{\hat{p}_{\text {in }}\left(\mathbf{z}_{i} ; k, n\right)<\frac{\beta \varepsilon \hat{c}_{0}}{(1-\beta)(1-\varepsilon)}\right\}$, and $\lambda=$ $-\sqrt[m-1]{\frac{(1-\beta)(1-\varepsilon) k}{\beta \varepsilon c_{b} n \hat{c}_{0}}}$, we have

（其中有很多参考文献，和相应的理论背景。考虑到理论推导的部分向来比较复杂，建议参考原文和相应的参考文献慢慢理解，就不做过多展开。该部分还是非常有意思的，解释了为什么这种非常直觉的方法可以取得这么好的效果。）

5. 结论¶

本文引入了第一个探索和证明非参数KNN方式，来研究OOD 检测的距离。 与以前的工作不同，非参数方法没有对底层特征空间施加任何分布假设，因此提供了更强的灵活性和通用性。该工作提供重要的高质量的特征嵌入和合适的距离测量是两个不可或缺的组成部分用于OOD检测任务。 大量实验表明基于 KNN 的方法可以显着提高性能在几个 OOD 检测基准上，取得了卓越的结果。 我们希望我们的工作能激发未来的研究使用非参数方法进行OOD检测。