YOLOv7来临：图解网络结构模块

【前言】此篇续上篇论文解读《YOLOv7来临：论文解读附代码解析》，对YOLOv7网络结构中的一些重要模块进行讲解。

一、ReOrg 操作¶

这个模块其实是对输入的信息进行切片操作，和YOLOv2的PassThrough层以及YOLOv5的focus操作类似，对输入图层尽可能保持原信息并进行下采样，相关代码如下:

class ReOrg(nn.Module):
    def __init__(self):
        super(ReOrg, self).__init__()

    def forward(self, x):  # x(b,c,w,h) -> y(b,4c,w/2,h/2)
        return torch.cat([x[..., ::2, ::2], x[..., 1::2, ::2], x[..., ::2, 1::2], x[..., 1::2, 1::2]], 1)

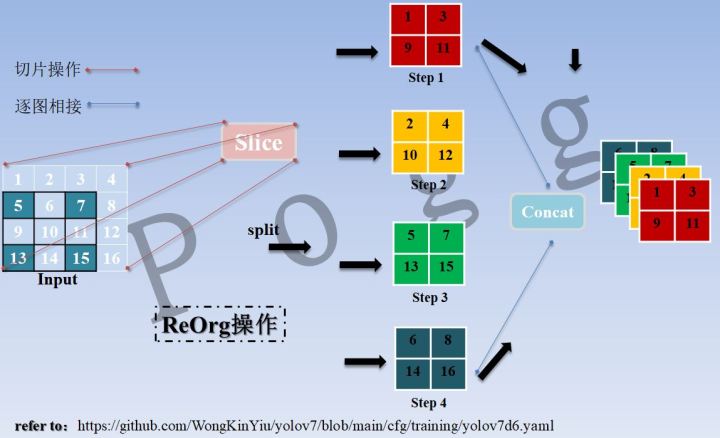
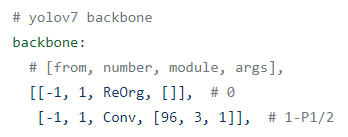
在YOLOv7仓库中，通过观察YOLOv7.yaml可以发现，原始的640 × 640 的图像进入ReOrg操作，先变成320 × 320的特征图，在通过拼接（Concat）后，会经过一次卷积（CBL）操作，最终变成320 × 320 × 96的特征图。

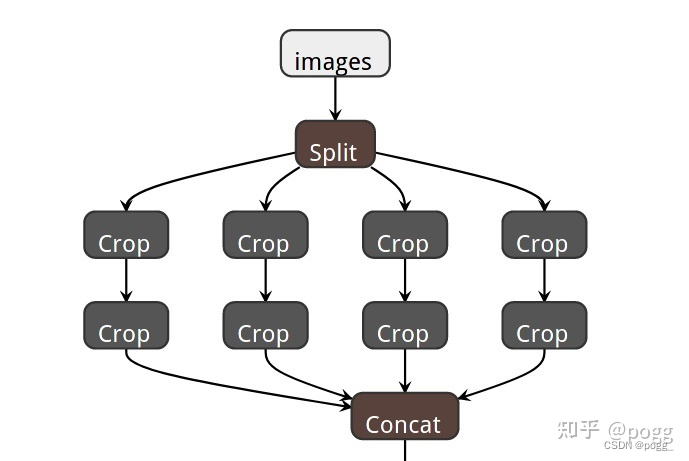
这个其实和YOLOv5几乎一致，不过从YOLOv5第六版开始后，已舍弃该操作，v5作者认为第一层采用6×6，stride＝2的常规卷积产生的参数更少，效果更好，原始的Focus层如下图:

二、多路卷积模块¶

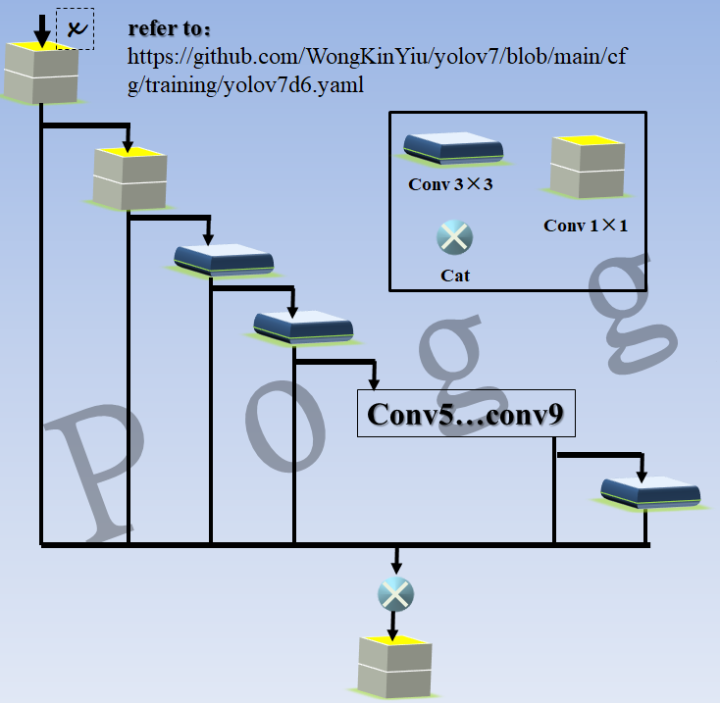
其实看到这里还是蛮震惊的，毕竟在论文中，作者在相关调研工作开展后，发现" Starting from the characteristics of memory access cost, Ma et al. [55] also analyzed the influence of the input/output channel ratio, the number of branches of the architecture, and the element-wise operation on the network inference speed. "，有一条提到多分支操作必然会降低运行效率（也有可能v7的作者是CSPNet的作者，能用该结构说明实验效果还是不错的)，这个多支路模块定义在yolov7d6.yaml配置文件中:

将上图的结构配置进行图解，类似下图，主要还是大量复用1×1的point conv和3×3的standard conv，每个conv的输出不仅作为下一个conv的输入，还会和所有其他的conv输出进行concat操作，这个操作和DenseNet类似（但是笔者认为这样的模块势必会造成训练耗时的增加)。

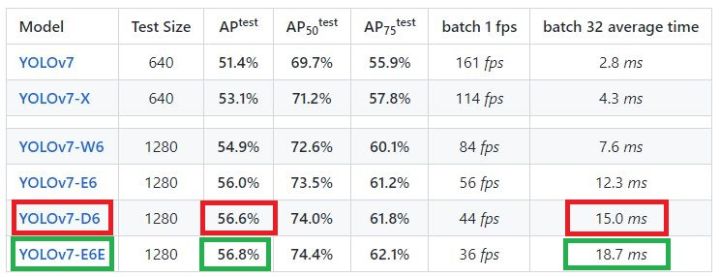
另外，可以看到下面一张关于各个模型的Benchmark性能图，input size=1280的模型普遍都使用了4个分支检测头，在模型列表中，显然包含了10 concat卷积的模块和E_ELAN模块的模型精度最高，但毫无疑问，多支路也造成了模型训练和推理耗时的增加，至于部署上线应该使用哪个模型比较合适，就仁者见仁智者见智了。

三、DownC模块¶

在讲这个模块前，需要先了解作者对同种最大池化层的两种定义:

• 对于定义一，将kernel_size和stride设为2的MaxPool2d称为MP；
• 对于定义二，将kernel_size设为3，stride设为1，并且填充padding的MaxPool2d称为SP

class MP(nn.Module):
    def __init__(self, k=2):
        super(MP, self).__init__()
        self.m = nn.MaxPool2d(kernel_size=k, stride=k)

    def forward(self, x):
        return self.m(x)

class SP(nn.Module):
    def __init__(self, k=3, s=1):
        super(SP, self).__init__()
        self.m = nn.MaxPool2d(kernel_size=k, stride=s, padding=k // 2)

    def forward(self, x):
        return self.m(x)

class DownC(nn.Module):
    # Spatial pyramid pooling layer used in YOLOv3-SPP
    def __init__(self, c1, c2, n=1, k=2):
        super(DownC, self).__init__()
        c_ = int(c1)  # hidden channels
        self.cv1 = Conv(c1, c_, 1, 1)
        self.cv2 = Conv(c_, c2//2, 3, k)
        self.cv3 = Conv(c1, c2//2, 1, 1)
        self.mp = nn.MaxPool2d(kernel_size=k, stride=k)

    def forward(self, x):
        return torch.cat((self.cv2(self.cv1(x)), self.cv3(self.mp(x))), dim=1)

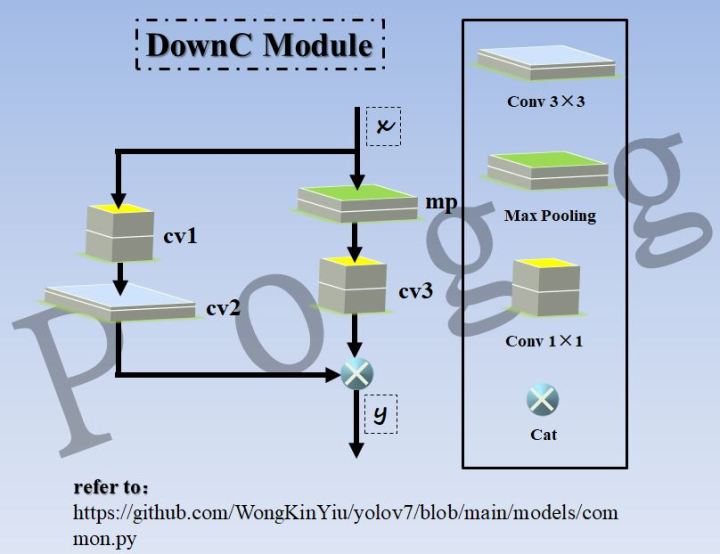
通过代码可以看到，DownC模块会用到三种最基本的结构，包括1×1的point conv，3×3的standard conv，以及mp操作的MaxPool，使用这三种基础模块组装成DownC大模块，对代码进行图解，如下:

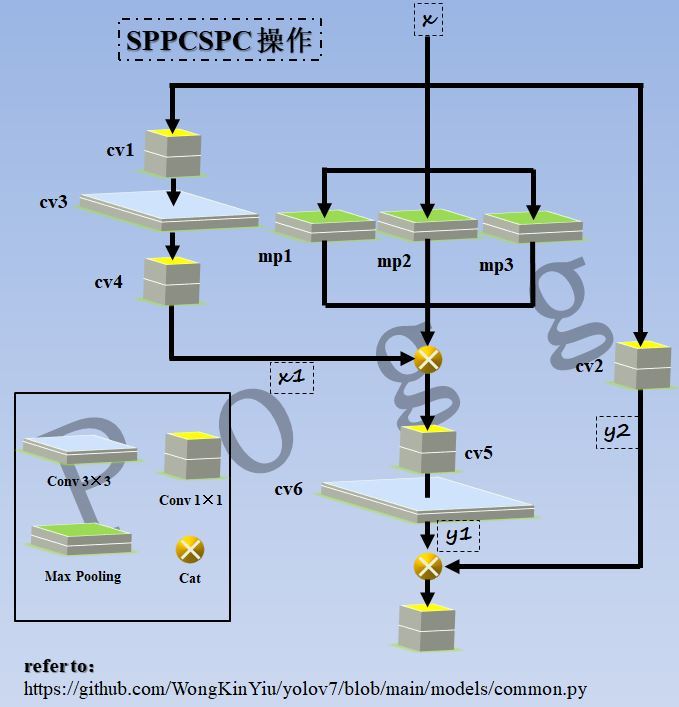
四、SPPCSPC模块¶

这是一种利用金字塔池化操作和CSP结构得到的模块，依旧包含了大量支路，官方给出的代码如下:

class SPPCSPC(nn.Module):
    # CSP https://github.com/WongKinYiu/CrossStagePartialNetworks
    def __init__(self, c1, c2, n=1, shortcut=False, g=1, e=0.5, k=(5, 9, 13)):
        super(SPPCSPC, self).__init__()
        c_ = int(2 * c2 * e)  # hidden channels
        self.cv1 = Conv(c1, c_, 1, 1)
        self.cv2 = Conv(c1, c_, 1, 1)
        self.cv3 = Conv(c_, c_, 3, 1)
        self.cv4 = Conv(c_, c_, 1, 1)
        self.m = nn.ModuleList([nn.MaxPool2d(kernel_size=x, stride=1, padding=x // 2) for x in k])
        self.cv5 = Conv(4 * c_, c_, 1, 1)
        self.cv6 = Conv(c_, c_, 3, 1)
        self.cv7 = Conv(2 * c_, c2, 1, 1)

    def forward(self, x):
        x1 = self.cv4(self.cv3(self.cv1(x)))
        y1 = self.cv6(self.cv5(torch.cat([x1] + [m(x1) for m in self.m], 1)))
        y2 = self.cv2(x)
        return self.cv7(torch.cat((y1, y2), dim=1))

五、RepConv模块¶

这个应该是今年最火的一种模型架构策略了，以前的设计范式提出了许多复杂而又高效的网络结构，但它们在真实设备中的表现往往不如预期，特别是对于算力匮乏的设备。RepVGG是一种基于VGG网络设计的多分支模型，在训练过程中可以通过多分支提升性能，推理可以通过结构重新参数化转换为具有3×3卷积和ReLU的连续直筒型VGG类网络，实现推理速度的加快。在现代卷积神经网络架构中，推理过程使用的某些特定硬件实现推理加速显得格外复杂和繁琐，与附加的定制硬件相比，直筒型VGG类网络有着简单，推理速度快的优势，如下所示:

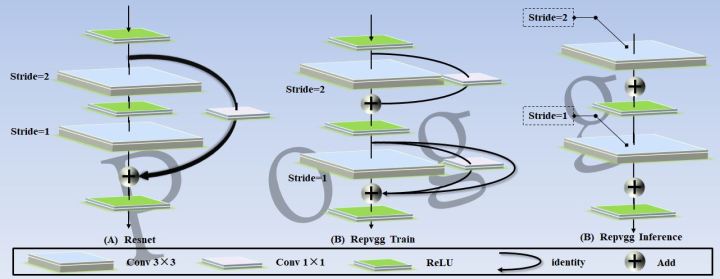
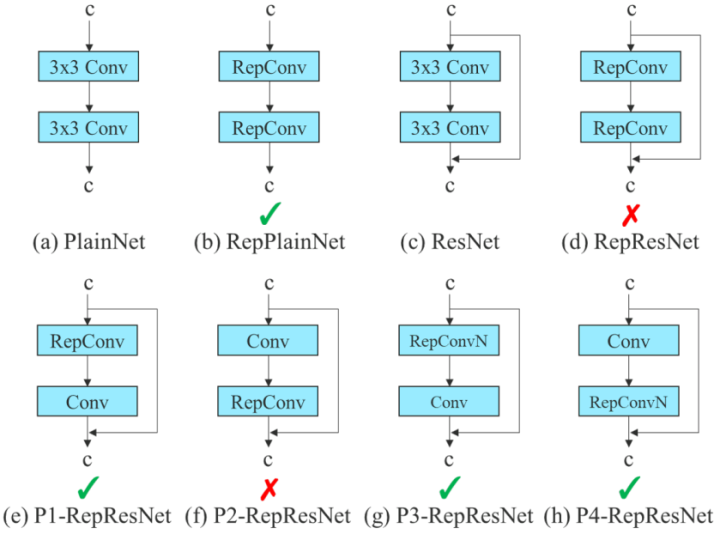
尽管RepConv在VGG上取得了优异的性能，但将它直接应用于ResNet和DenseNet或其他网络架构时，它的精度会显著降低。作者使用梯度传播路径来分析不同的重参化模块应该和哪些网络搭配使用。通过分析RepConv与不同架构的组合以及产生的性能，作者发现RepConv中的identity破坏了ResNet中的残差结构和DenseNet中的跨层连接，这为不同的特征图提供了梯度的多样性。基于上述原因，作者使用没有identity连接的RepConv结构。图4显示了作者在PlainNet和ResNet中使用的“计划型重参化卷积”的一个示例。

E-ELAN模块¶

在大多数关于设计高效网络的论文中，主要考虑的因素是参数量、计算量和计算密度。但从内存访存的角度出发出发，还可以分析输入/输出信道比、架构的分支数和元素级操作对网络推理速度的影响（shufflenet论文提出)。在执行模型缩放时还需考虑激活函数，即更多地考虑卷积层输出张量中的元素数量。因此，在本文中，作者提出了基于ELAN的扩展版本E-ELAN，其主要架构如图2(d)所示。

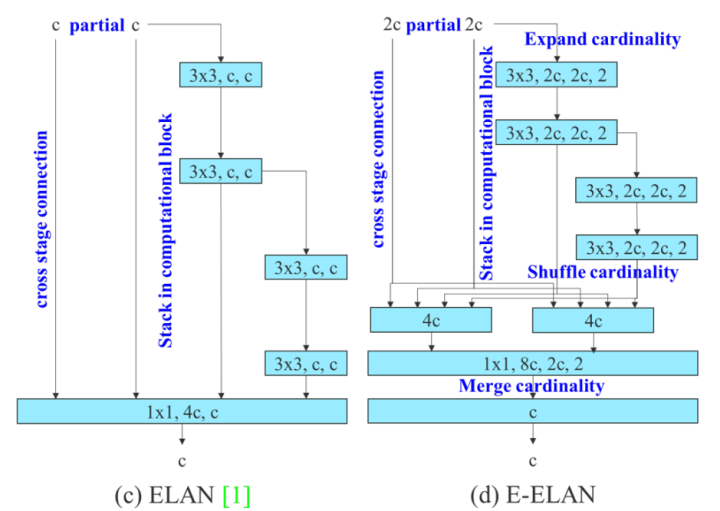
在大规模ELAN中，无论梯度路径长度和计算模块数量如何，都达到了稳定的状态。但如果更多计算模块被无限地堆叠，这种稳定状态可能会被破坏，参数利用率也会降低。本文提出的E-ELAN采用expand、shuffle、merge cardinality结构，实现在不破坏原始梯度路径的情况下，提高网络的学习能力。但是笔者找了整个common.py文件，似乎没有找到定义这个模块的代码，不过在yolov7-e6e.yaml中找到了拆散成单独算子的结构配置，如下:

然而，找了一圈，貌似没看到作者在论文中提到的merge cardinality和shuffle cardinality等操作，此处蹲坑。

总结¶

此篇续上篇博客《YOLOv7来临：论文解读附代码解析》，对YOLOv7网络结构中的一些重要模块进行学习，但在结尾处附加笔者的几处疑问，例如:

• 论文中提到的SiLU函数在官方仓库中并未见到
• YOLOv7-Tiny目前仅提供了SiLU版本，未提供论文中的ReLU版本
• 官方仓库所使用的激活函数统一为LeakyReLU
• 目前暂未在仓库中找到论文中提到的merge cardinality和shuffle cardinality等操作
• 作者在论文提及多分支结构的弊端，但在模型中依旧使用类似densenet多分支，应该是实验出该模型在gpu架构上高效，但训练以及在低算力平台（此处指量化4bit后的版本)的速度问题有待商榷。

目前仓库还在频繁更新，期待作者后期给出的惊喜，另外在网络结构yaml配置文件将层拆的如此精细，笔者认为最快在一个月内，YOLOv7将提供Darknet框架的cfg模型配置文件，以适配Darknet框架的训练，和YOLOv4进行大一统。