1. 前言¶

看到这个题目想必大家都猜到了，昨天的文章又有问题了。。。今天，又和两位大佬交流了一下YOLOV3损失函数，然后重新再对源码进行了梯度推导我最终发现，我的理解竟然还有一个很大的错误，接下来我就直入主题，讲讲在昨天文章放出的损失函数上还存在什么错误。

2. 回顾¶

上篇文章的地址是：你对YOLOV3损失函数真的理解正确了吗？ ，然后通过推导我们将损失函数的表示形式定格为了下面的等式：

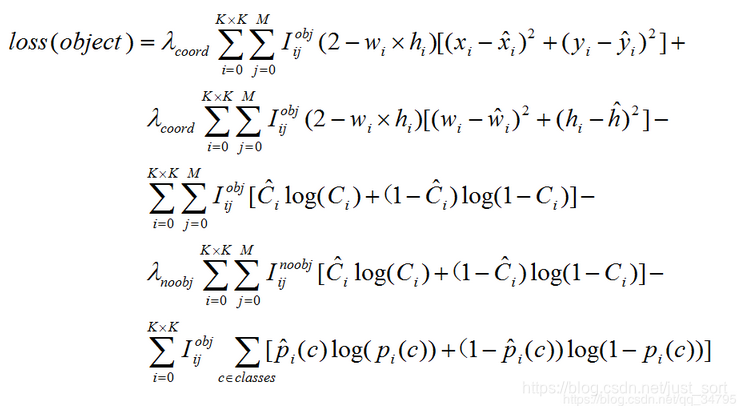
那么这个等式还存在什么问题呢？

答案就是DarkNet中坐标损失实际上是BCE Loss而不是这个公式写的MSE Loss。

3. 打个问号？¶

我们首先定位一下源码的forward_yolo_layer_gpu函数：

可以看到$x,y,w,h$在计算损失函数之前先经过了Logistic回归，也就是一个Sigmoid函数进行激活然后再计算损失，如果这个损失如上面的公式所说是MSE Loss的话，那么我们来推导一下梯度。

按照上面的公式，坐标的损失函数可以表达为$loss=\frac{1}{2}(y-sigmoid(x))^2$，其中$x$代表坐标表示中的任意一个变量，那么我们来求一下偏导，根据链式法则可以得到：

$\frac{d loss}{dx}=-(y-sigmoid(x))*(1-x)*x$，其中$x*(1-x)$是$sigmoid(x)$对$x$的倒数，进一步将其整理为：

$\frac{d loss}{dx}=(sigmoid(x)-y)*(1-x)*x$

又因为DarkNetdarknet是直接weights+lr*delta，所以是实际算的时候梯度是上面等式的相反数，所以：

$\frac{d loss}{dx}=(y-sigmoid(x))*(1-x)*x$

然后我们看一下官方DarkNet源码对每个坐标的梯度表达形式：

前面的scale就是$2-w*h$我们暂时不看，可以看到梯度的形式就是一个$y-sigmoid(x)$呀（注意在forward_yolo_layer_gpu函数中执行的是$x=sigmoid(x)$操作，这里为了方便理解还是写成$sigmoid(x)$），所以我有了大大的问号？

Sigmoid函数的梯度去哪了？？？

4. 解除疑惑¶

有一个观点是其实YOLOV3的坐标损失依然是BCE Loss，这怎么和网上的博客不一样啊（所以啊，初期可以看博客，学习久了就要尝试脱离博客了），那么我们带着这个想法来推导一番。

我们知道对于BCE Loss来说：

$loss = - y'*log(y)-(1-y')*log(1-y)$

这里$y'$表示标签值，那么自然有$y=sigmoid(x)$

所以这里我们就变成了求loss对$x$的导数：

$\frac{\partial loss}{\partial x}=(\frac{-y'}{y}+\frac{1-y'}{1-y})\frac{\partial y}{\partial x}$

$\frac{\partial loss}{\partial x}=(\frac{-y'}{y}+\frac{1-y'}{1-y})*y*(1-y)$

$\frac{\partial loss}{\partial x}=y(1-y')-y'(1-y)$

$\frac{\partial loss}{\partial x}=y-y'$

又因为DarkNetdarknet是直接weights+lr*delta，所以是实际算的时候梯度是上面等式的相反数，所以：

$\frac{\partial loss}{\partial x}=y'-y$

回过头看一下DarkNet在坐标损失上的梯度呢？

这不是一模一样？ 根据梯度来判断，坐标损失是BCE损失没跑了吧。

5. 总结¶

通过对梯度的推导，我们发现DarkNet官方实现的YOLOV3里面坐标损失用的竟然是BCE Loss，而YOLOV3官方论文里面说的是MSE Loss，我个人觉得论文不能全信啊233。

至此DarkNet中YOLO V3的损失函数解析完毕，只需要将

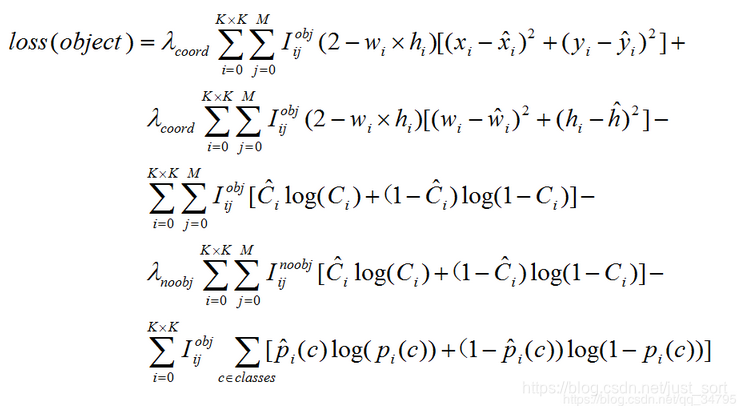
这里面的MSE坐标损失替换成BCE坐标损失就可以获得最终的DarkNet YOLOV3的损失函数啦。

6. 参考¶

• https://blog.csdn.net/qq_34795071/article/details/92803741
• https://pjreddie.com/media/files/papers/YOLOv3.pdf
• https://github.com/pjreddie/darknet/blob/master/src/yolo_layer.c

欢迎关注GiantPandaCV, 在这里你将看到独家的深度学习分享，坚持原创，每天分享我们学习到的新鲜知识。( • ̀ω•́ )✧

有对文章相关的问题，或者想要加入交流群，欢迎添加BBuf微信：

为了方便读者获取资料以及我们公众号的作者发布一些Github工程的更新，我们成立了一个QQ群，二维码如下，感兴趣可以加入。