大疆腾讯携手杀疯了！——单目深度估计挑战赛冠军方案-ICCV2023¶

1.论文摘要：¶

利用图像进行精确3D场景重建是一个存在已久的视觉任务。由于单图像重建问题的不适应性，大多数成熟的方法都是建立在多视角几何之上。当前SOTA单目度量深度估计方法只能处理单个相机模型，并且由于度量的不确定性，无法进行混合数据训练。与此同时，在大规模混合数据集上训练的SOTA单目方法，通过学习仿射不变性实现了零样本泛化，但无法还原真实世界的度量。本文展示了从单图像获得零样本度量深度模型，其关键在于大规模数据训练与解决来自各种相机模型的度量不确定性相结合。作者提出了一个规范相机空间转换模块，明确地解决了不确定性问题，并可以轻松集成到现有的单目模型中。配备该模块，单目模型可以稳定地在数以千计的相机型号采集的8000万张图像上进行训练，从而实现对真实场景中从未见过的相机类型采集的图像进行零样本泛化。

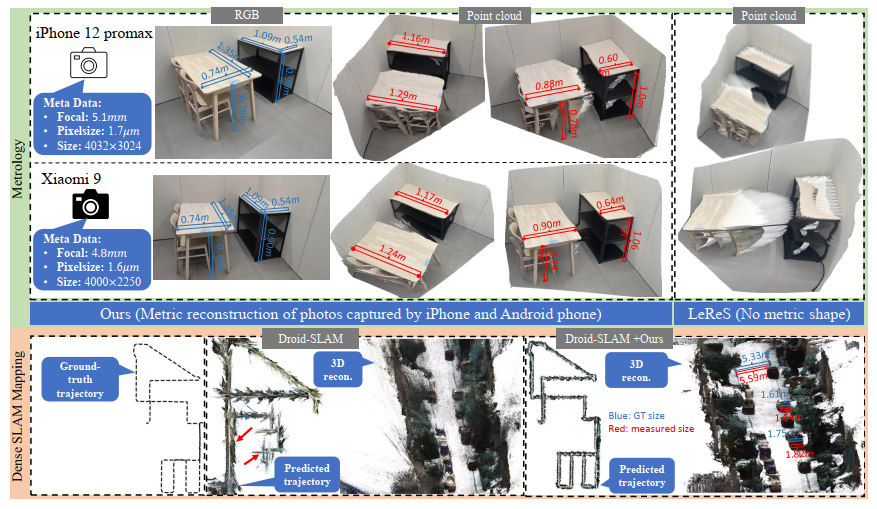
图1的说明：顶部（测距）：我们使用两部手机(iPhone 12和一部安卓手机)来拍摄场景，并测量桌子的大小。通过照片的元数据，我们执行3D度量重建，然后测量桌子的大小(标记为红色)，这非常接近真值(标记为蓝色)。与此形成对比，最近的方法LeReS 的表现要差得多，并且按照设计无法预测度量3D。底部(密集SLAM建图)：现有的SOTA单目SLAM方法通常在大规模场景中面临尺度漂移问题(见红色箭头)，并且无法达到度量尺度，而未经处理地输入我们的度量深度模型，Droid-SLAM 可以恢复更精确的轨迹并执行度量密集映射(见红色测量)。注意，所有测试数据对我们的模型来说都是未见的。

实验表明该方法在7个零样本基准测试中都取得了SOTA性能。值得注意的是，该方法赢得了第二届单目深度估计挑战赛冠军。该方法可以从随机收集的互联网图像中准确重构3D度量结构，为单图像测距开辟了道路。潜在的益处可以延伸到通过简单地使用此模型来显著改进的下游任务。例如，此模型缓解了单目SLAM系统的尺度漂移问题(图1)，实现了高质量的度量尺度密集映射。

代码未来发布地址：https：//github.com/YvanYin/Metric3D。

原文链接：https：//arxiv.org/abs/2307.10984

2.方案简介¶

通过作者提出的方法，可以轻松将模型训练扩展到自数以万计的不同相机采集的11个数据集的800万张图像，覆盖各种室内外场景，实现零样本可转移并保持高准确性。此模型可以在从随机收集的互联网图像中准确重构3D度量结构，实现可信的单图像测距。与仿射不变深度模型不同，此模型也可以直接提高各种下游任务质量。例如(图1所示)，借助此模型预测的度量深度，可以显著减少单目SLAM 系统的尺度漂移，实现更好的映射质量和真实世界度量恢复。此模型还支持大规模3D重建。该模型在第二届单目深度估计挑战赛中获得冠军。总之，本项目的主要贡献有：

1.提出了规范和去规范相机转换方法，以解决来自各种相机设置的度量深度不确定性问题。它可以从大规模数据集中学习强大的零样本单目度量深度模型。

2.提出了一个随机建议规一化损失来有效提高深度准确性;

3.此模型在7个零样本基准测试中均达到了SOTA性能。它可以执行高质量的现实场景3D度量结构恢复，并改进几个下游任务，如单目SLAM 、3D场景重建和测距。

3.方法详解¶

预备知识。考虑具有内在参数的针孔相机模型：[[$\hat{f}/\delta$ ， 0 ， $u_0$]，[ 0 ， $\hat{f}/\delta$，$ v_0$]，[0 ， 0 ， 1]] ，其中，$\hat{f}$是焦距(以微米为单位)，$\delta$是像素大小(以微米为单位)，($u_0$，$v_0$)是原则中心。$f=\hat{f}/\delta$ 是视觉算法中使用的以像素表示的焦距。

3.1 度量不确定性分析¶

图3给出了不同相机在不同距离拍摄的示例照片。仅从图像外观，人们可能会认为后两个照片是使用相同的相机在相似的位置拍摄的。事实上，由于焦距不同，它们是在不同的位置拍摄的。因此，在仅从单个图像进行度量估计时，相机内在参数至关重要，否则问题是无法得到唯一解的。为避免这样的度量不确定性，近期的方法(如MiDaS 和LeReS )在监督过程中分离度量，并折中学习仿射不变深度。

图4(A)显示了一个简单的针孔透视投影。目标A位于$d_a$被投影到A'。根据相似原理，有方程：

$d_a=\hat{f}\frac{\hat{S}_h}{\hat{S}_i'}=\hat{f}\hat{S}\alpha$ (1)

其中，$\hat{S}$和$\hat{S}'$分别是真实大小和成像大小。$\hat{}$表示变量在物理度量下(例如，毫米)。要从单个图像中恢复$d_a$，必须知道焦距、目标的成像大小和真实世界目标大小。估计焦距是一个从单个图像难以确定和无唯一解问题。在此，通过假设训练/测试图像的焦距是可用的来简化问题。相比之下，理解成像大小对神经网络来说要容易得多。为了获得真实世界的目标大小，神经网络需要理解场景布局和目标语义，这是神经网络的强项。定义$\alpha=\hat{f}/\hat{S}'$，所以$d_a$与$\alpha$成比例。

对传感器大小、像素大小和焦距做以下观察。

O1：传感器大小和像素大小不会影响度量深度估计。基于透视投影(图4 (A))，传感器大小仅影响视场(FOV)，与$\alpha$无关，因此不会影响度量深度估计。对于像素大小，假设两个相机具有不同的像素大小($\delta_1=2\delta_2$)但相同的焦距$\hat{f}$在同一距离$d_a$拍摄相同的目标。图4(B)显示它们拍摄的照片。根据预备知识，$f_1=2f_2$。由于第二个相机具有更小的像素大小，尽管在相同的成像大小$\hat{S}'$下，像素表示的图像分辨率为$S_1'=\frac{1}{2}S_2'$。根据式(1)，$\frac{\hat{f}}{\delta_1}S_1'=\frac{\hat{f}}{\delta_2}S_2'$，即$\alpha_1=\alpha_2$，所以$d_1=d_2$。因此，不同的相机传感器不会影响度量深度估计。

O2：焦距对度量深度估计至关重要。图3显示由未知焦距引起的度量不确定性问题。图5进行了说明。如果两个相机($f_1=2f_2$)分别在$d_1=2d_2$的距离，成像大小在两个相机上的成像大小相同。因此，仅从外观，当用不同的标签进行监督时，网络会出现不确定性。基于这一观察，提出规范相机转换方法来解决监督和图像表观冲突。

3.2 规范相机转换¶

核心思想是建立一个规范相机空间(($f_x^c$，$f_y^c$)，实验中设置$f_x^c=f_y^c=f_c$)，并将所有训练数据转换到此空间。因此，所有数据可以粗略地看作是由规范相机捕获的。作者提出了两种变换方法，即转换输入图像(I∈R$^{H×W×3}$)或转换真值(GT)(D∈R$^{H×W}$)。原始内参为{$f$，$u_0$，$v_0$}。

方法1：转换深度标签(CSTM标签)。图3的不确定性是因为深度。因此的第一种方法直接转换真值深度以解决这个问题。具体地，在训练中用比例$\omega_d=\frac{f_c}{f}$缩放真值深度$(D*)$，即$D_c^*=\omega_dD^*$。原始相机模型转换为{$f_c$，$u_0$，$v_0$}。在推理中，预测深度(D$_c$)在规范空间中，需要执行去规范变换来恢复度量信息，即D=$\frac{1}{\omega_d}$D$_c$。注意输入I不执行任何变换，即I$_c$=I。

方法2：转换输入图像(CSTM图像)。从另一角度来看，不确定性是由相似的图像表观造成的。因此，此方法是转换输入图像以模拟规范相机的成像效果。具体地，用比例$\omega_r=\frac{f_c}{f}$调整图像大小I，即I$_c$=T(I，$\omega_r$)，其中T(·)表示图像调整大小。光心大小也被调整，因此规范相机模型为{$f_c$，$\omega_ru_0$，$\omega_rv_0$}。真值标签无任何缩放调整大小，即D$^*_c$=T(D*，$\omega_r$)。在推理中，去规范变换是不调整尺度将预测还原到原始大小，即D=T(D$_c$，$\frac{1}{\omega_r}$)。

图2显示了流程图。执行任一变换后，随机裁剪修补进行训练。裁剪仅调整FOV和光心，因此不会引起任何度量不确定性问题。在标签变换方法中$\omega_r=1$和$\omega_d=\frac{f_c}{f}$，而在图像变换方法中$\omega_d=1$和$\omega_r=\frac{f_c}{f}$。训练目标如下：

$\min_\theta|N_d(I_c，\theta)-D_c^*|$ (2)

其中$\theta$是网络(N$_d$(·))的参数，D$^*_c$和I$_c$分别是变换后的真值深度标签和图像。

混合数据训练是提升泛化能力的有效方法。作何收集了11个数据集进行训练。在混合数据中，包含了10，000多种不同的相机。所有收集的训练数据都包括配对的相机内参，在规范变换模块中使用。

监督。为进一步提升性能，作者提出了随机建议归一化损失(RPNL)。尺度位移不变损失被广泛应用于仿射不变深度估计，它分离深度尺度以强调单个图像的分布。但是，它们在整个图像上执行，不可避免地会压缩细粒度的深度差异。受此启发，作者从真值D$^*_c$和预测深度D$_c$中随机裁剪若干补丁(p$_{i}$，i=0，...，M)∈R$^{h_i×w_i}$。然后对成对的补丁执行中值绝对偏差归一化。归一化局部统计数据可以增强局部对比度。随机建议归一化损失函数如下：

$\begin{aligned}L_{\mathrm{RPNL}}&=\frac{1}{MN}\sum_{p_i}^M\sum_{j}^N|\frac{d_{p_i，j}^*-\mu(d_{p_i，j}^*)}{\frac{1}{N}\sum_{j}^N|d_{p_i，j}^*-\mu(d_{p_i，j}^*)|}-\frac{d_{p_i，j}-\mu(d_{p_i，j})}{\frac{1}{N}\sum_{j}^N|d_{p_i，j}-\mu(d_{p_i，j})|}|\end{aligned}$

其中，$d*∈D^*_c$和$d∈D_c$分别是真值和预测深度。$\mu(·)$是深度的中值。M是建议裁剪的数量，设置为32。在训练期间，建议以原始大小的0.125到0.5随机从图像中裁剪。此外，还采用其他几个损失，包括对数尺度不变损失L$_{silog}$，成对的正常回归损失L$_{PWN}$，虚拟法线损失L$_{VNL}$。注意L$_{silog}$是L1损失的变体。总体损失如下：

L=L$_{PWN}$+L$_{VNL}$+L$_{silog}$+L$_{RPNL}$

4.结果对比¶

作者对几个NYUv2场景进行了采样，以进行3D重建比较。由于作者的方法可以预测准确的度量深度，因此所有帧的预测都融合在一起进行场景重建。相比之下，LeReS的深度达到了未知的尺度和偏移，这会导致明显的失真。DPSNet是一种多视图立体方法，不能很好地处理低纹理区域。

5.受益的下游任务¶

6.结论¶

在本文中，作者解决了从单个单目图像重建3D度量场景的问题。为解决各种焦距导致的图像表观中的深度不确定性，作者提出了规范相机空间变换方法。借助该方法，可以轻松地将训练扩展到从10000多个相机采集11个数据集中的800万幅图像，实现零样本转移和高准确性度量。此模型可以在随机收集的互联网图像中准确重构3D度量结构，并使几种下游任务受益，例如单目SLAM 、3D场景重建和测距等等。