跳转至

CVPR 2023 中的半监督学习: FixMatch 的升级版 UniMatch

目录

  • 前言
  • UniMatch 概述
  • 回顾 FixMatch
  • 统一图像和特征的扰动
  • 双流扰动
  • 实验
  • 总结
  • 参考

前言

我们首先回顾下发表在 NeurIPS 2020 上的 FixMatch: Simplifying Semi-Supervised Learning with Consistency and Confidence，FixMatch 是一种更轻量的半监督分类方法。如下图所示，FixMatch 首先使用模型（带标签数据训练后的）对弱增强的未标记图像进行预测，生成伪标签。对于给定的图像，只有在模型产生高置信度的预测时，伪标签才会被保留。然后，在输入同一图像的强增强版本时，训练模型预测伪标签。

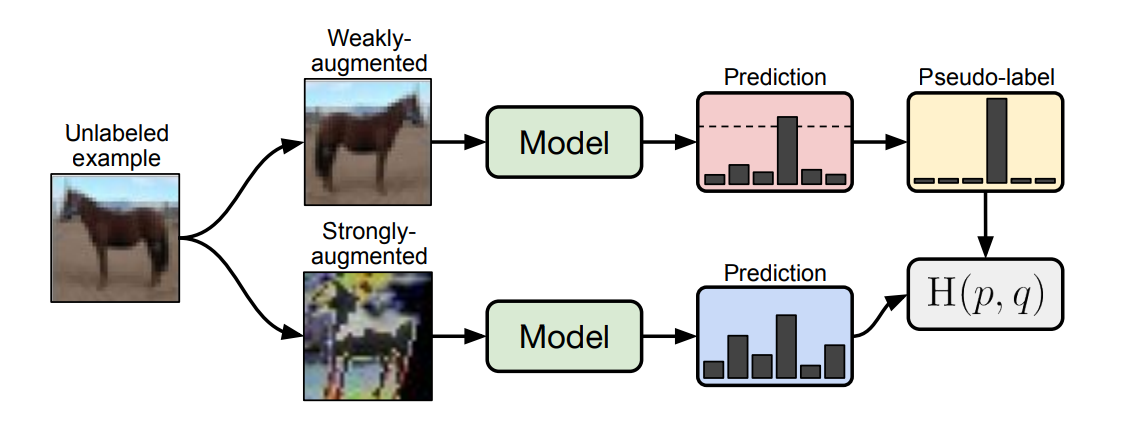
请添加图片描述

有趣的是，这样一个简单的流程在转移到分割场景中已经取得了与最近的先进工作相近的结果。然而，它的成功在很大程度上依赖于对强数据增强的手动设计。出于这个动机，这篇文章提出了一个辅助特征扰动流作为补充，从而扩大了扰动空间（特征级别）。另一方面，为了充分探索原始图像级别的增强，提出了一种双流扰动技术，使两个强视图同时由一个共同的弱视图引导（可以理解为增大 FixMatch 的强增强分支数量）。

下面我们正式开始 UniMatch 的介绍。

UniMatch 概述

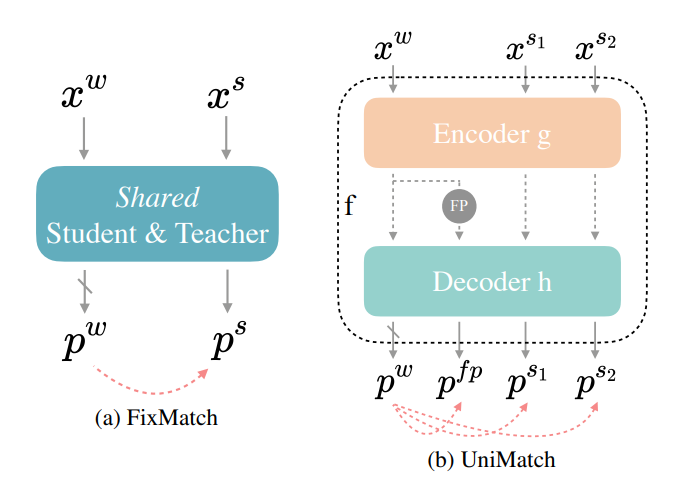
下图（a）表示普通的 FixMatch，x^w 代表弱增强，x^S 代表强增强。在 FixMatch 的基础上，UniMatch 将图像级和特征级扰动以独立流的形式统一起来，以探索更广泛的扰动空间，采用一种双流扰动策略，充分探索预定义的图像级扰动空间，并利用对比学习的优点来获取有区分度的表示。下图（b）中，p^{f p} 表示特征级扰动，p^{s_1} 和 p^{s_2} 表示双流图像级扰动。 请添加图片描述

回顾 FixMatch

FixMatch 利用弱到强的一致性正则化方法来利用未标记的数据。它将每个未标记图像同时经过弱扰动和强扰动，然后通过有监督损失和无监督损失的组合进行模型优化。其中，无监督损失通过强扰动下的预测与弱扰动下的预测相同来约束模型的学习，无监督损失的定义如下： $$ \mathcal{L}_u=\frac{1}{B_u} \sum \mathbb{1}\left(\max \left(p^w\right) \geq \tau\right) \mathrm{H}\left(p^w, p^s\right) $$ 上面的公式中，τ 是预定义的置信度阈值，用于过滤噪声标签，H 用于最小化两个概率分布之间的熵。

p^w 和 p^s 的定义如下： $$ pw=\hat{F}\left(\mathcal{A}w\left(x^u\right)\right) ; \quad ps=F\left(\mathcal{A}s\left(\mathcal{A}w\left(xu\right)\right)\right) $$ 教师模型 F^ 在弱扰动图像上生成伪标签，而学生模型 F 利用强扰动图像进行模型优化。在 UniMatch 中，为了简化起见，将 F^ 设置为与 F 完全相同，遵循 FixMatch 的做法（即 Shared）。

统一图像和特征的扰动

FixMatch 的优化只在图像级别上，为了构建一个更广泛的扰动空间，在 FixMatch 的基础上，UniMatch 在弱扰动图像 x^w 的特征层上注入了扰动，如下图（a）所示。每个未标记的小批量数据维持三个前馈流：最简单的流程 x^w → f → p^w，图像级强扰动流程 x^S → f → p^s ，以及引入的特征扰动流程 x^w → g → P → h → p^{f p}。通过这种方式，学生模型在图像和特征级别都被强制保持扰动的一致性。文章中将其命名为 UniPerb。

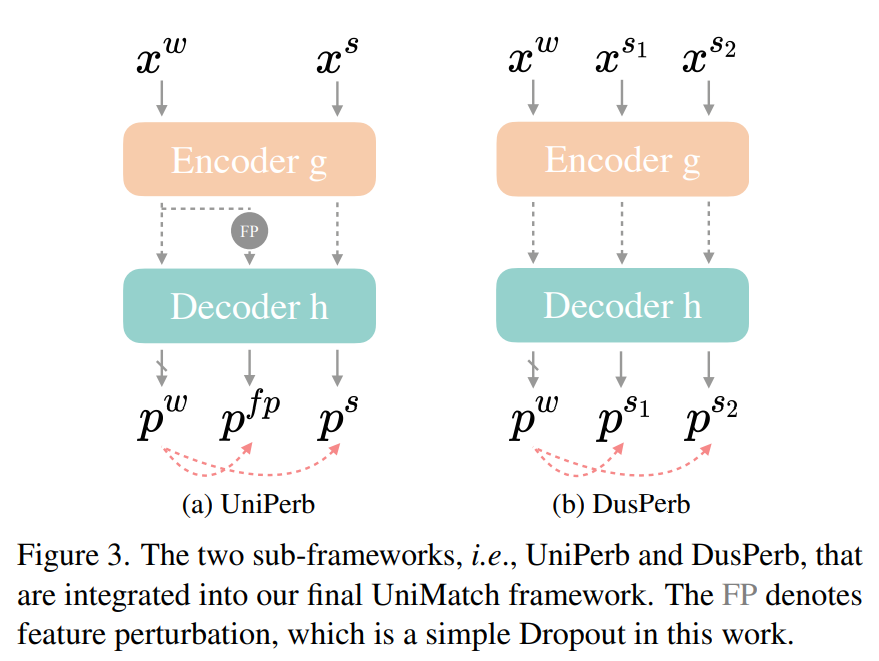
请添加图片描述

图（a）中 FP 的定义如下：

\begin{aligned} e^w & =g\left(x^w\right) \\ p^{f p} & =h\left(\mathcal{P}\left(e^w\right)\right), \end{aligned} $$ 其中，$e^w$ 是 $x^w$ 的提取特征，P 表示特征扰动，例如 dropout 或添加均匀噪声。无监督损失 Lu 的定义如下，和 FixMatch 最朴素的无监督损失对比，增加了 $p^w$ 和 $p^{f p}$ 两个概率分布之间的熵。 $$ \mathcal{L}_u=\frac{1}{B_u} \sum \mathbb{1}\left(\max \left(p^w\right) \geq \tau\right)\left(\mathrm{H}\left(p^w, p^s\right)+\mathrm{H}\left(p^w, p^{f p}\right)\right)

双流扰动

双流扰动的示意图如上图（b）所示，使用两个图像级别的扰动，用共同的弱视图约束两个强视图的一致性。文章中表示，这个操作还可以看作是在这两个强视图之间强制保持一致性。直观地说，假设有 k_w 是由 x^w 预测的类别的分类器权重，\left(q_{s_1}, q_{s_2}\right) 是图像 \left(x^{s_1}, x^{s_2}\right) 的特征，那么在采用的交叉熵损失中，我们最大化 q_j \cdot k_w 与 \sum_{i=0}^C q_j \cdot k_i 的值，其中 j \in\left\{s_1, s_2\right\}，k_i 是类别 i 的分类器权重。因此，我们也在最大化 q_{s_1} 和 q_{s_2} 之间的相似性。因此，看起来满足 InfoNCE 损失： $$ \mathcal{L}{s_1 \leftrightarrow s_2}=-\log \frac{\exp \left(q{s_1} \cdot q_{s_2}\right)}{\sum_{i=0}^C \exp \left(q_j \cdot k_i\right)}, \text { s.t., } j \in\left{s_1, s_2\right} $$ 其中 q_{s_1} 和 q_{s_2} 是正样本对，而除了 k_w 以外的所有其他分类器权重都是负样本。因此，它与对比学习相似，能够学习具有区分性的表示。以上这个步骤在文章中被称为 DusPerb。

综上所述，为了利用未标记的图像，提出了两个关键技术，即 UniPerb 和 DusPerb。UniMatch 将这两种方法整合在一起，总损失如下： $$ \begin{aligned} \mathcal{L}_u & =\frac{1}{B_u} \sum \mathbb{1}\left(\max \left(p^w\right) \geq \tau\right) . \ & \left(\lambda \mathrm{H}\left(p^w, p^{f p}\right)+\frac{\mu}{2}\left(\mathrm{H}\left(p^w, p{s_1}\right)+\mathrm{H}\left(pw, p^{s_2}\right)\right)\right) . \end{aligned} $$

实验

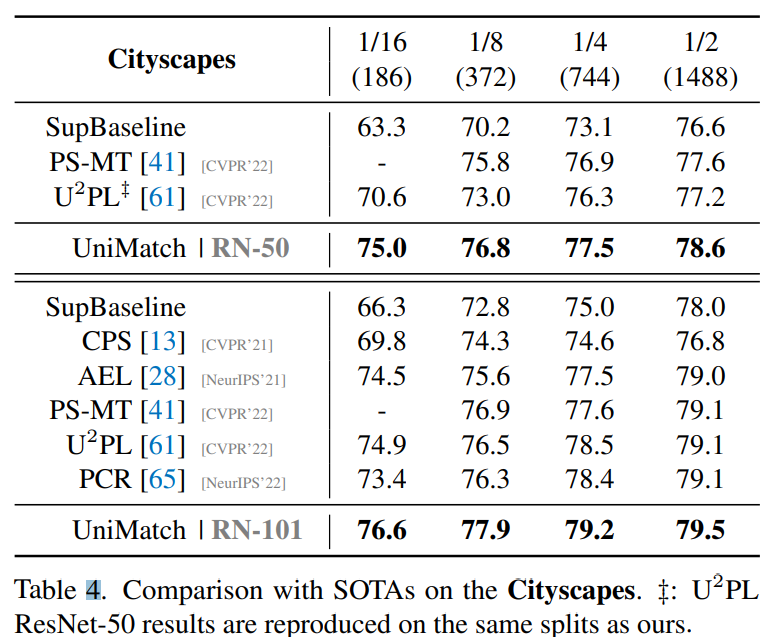
作者在不仅在自然图像上测试了半监督的结果，还在医学图像和遥感图像上做了实验。下表是在 Cityscapes 数据集上和其他 SOTA 方法的比较，并测试了两种backbone，在 1/16 数据集上，UniMatch 有了很大的提升。

请添加图片描述

COCO 数据集上的结果如下表：

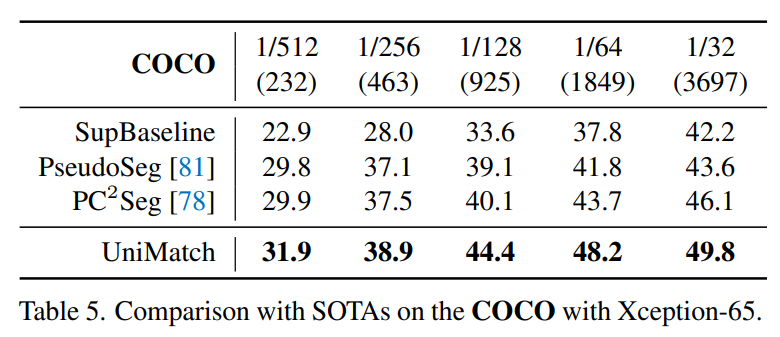
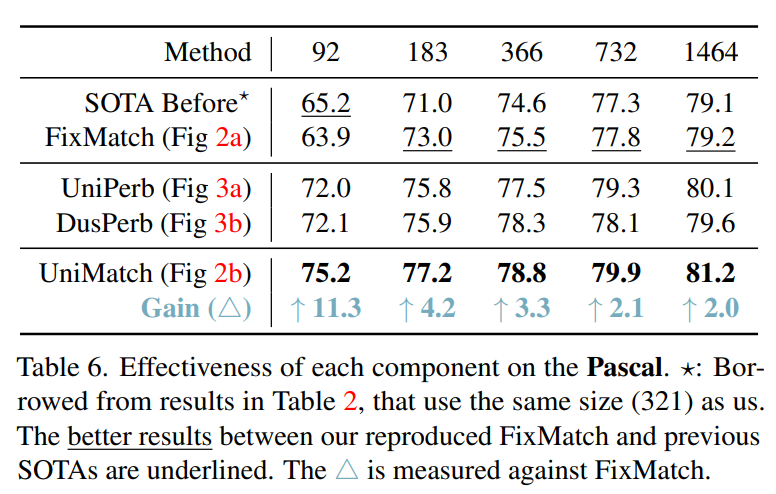
请添加图片描述

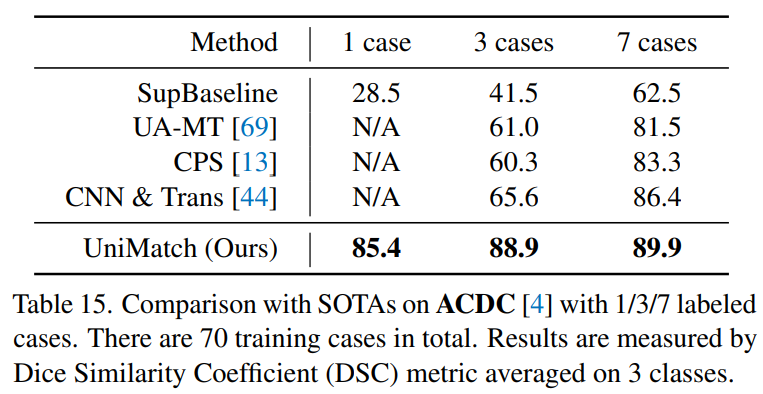
Pascal VOC 数据集上的结果如下表，这里对比了 FixMatch 的提升，在 92 张图像上，性能提升超过 10%。 请添加图片描述

下表是在医学图像 ACDC 数据集上的结果，对比其他半监督方法，UniMatch 只用了一个 case 就取得了非常高的结果。

请添加图片描述

总结

这篇文章研究了 FixMatch 在半监督语义分割中的作用，并发现配备适当的图像级强扰动后，基本的 FixMatch 方法可以超越现有的半监督分割方法。在此基础上，这篇文章进一步加强了扰动方法，通过统一图像级和特征级扰动。并设计了双流扰动技术，充分利用图像级扰动。这两个组件显著改进了 baseline，最终的 UniMatch 方法在各种场景中都取得了不错的效果。从UniMatch 实现思路上看，也可以做更好的知识蒸馏。文章中总结了四点现有工作的展望：（1）如何充分利用置信度低的像素；（2）伪标记中的类别不平衡；（3）标注与未标注伪标记的域偏差；（4）大规模半监督学习（pre-training 和 self-training）。

参考

本文总阅读量次