“北大-鹏城-腾讯”新视角：从势能的角度探讨模型的可迁移性-ICCV2023开源¶

1. 摘要¶

随着大规模数据集预训练模型的广泛应用，迁移学习已成为计算机视觉任务中的关键技术。但是，从大量的预训练模型库中为特定下游任务选择最优的预训练模型仍然是一个挑战。现有的方法主要依赖于编码的静态特征与任务标签之间的统计相关性来测量预训练模型的可迁移性，但它们忽略了微调过程中潜在的表示动力学的影响，导致结果不可靠，尤其是对于自监督模型。在本文中，我们从潜在能量的角度提出了一种新颖的方法——PED，来解决这些挑战。我们将迁移学习动力视为降低系统潜在能量的过程，并直接对影响微调动力学的相互作用力进行物理学建模。通过在物理驱动模型中捕获动态表示的运动来降低潜在能量，我们可以获得增强和更稳定的观测结果来估计可迁移性。在10个下游任务和12个自监督模型上的实验结果表明，我们的方法可以顺利集成到现有的优秀技术中，增强它们的性能，这揭示了它在模型选择任务中的有效性和发掘迁移学习机制的潜力。我们的代码将在https://github.com/lixiaotong97/PED上开源。

我们的主要贡献包括:

(1) 我们首次从潜在能量的角度重新审视迁移学习，并提出了一种物理驱动的方法来模拟迁移学习中的表征动力学。

(2) 我们设计了一种基于势能下降的方法，将每个类别的表征视为一个球，利用间隔力模拟类别之间的相互作用，从而捕获动态表示。

(3) 我们的方法可以轻松集成到现有方法中，在10个下游任务和12个自监督模型上的实验结果表明，我们的方法可以提升各种指标，为模型选择提供更准确的预测。

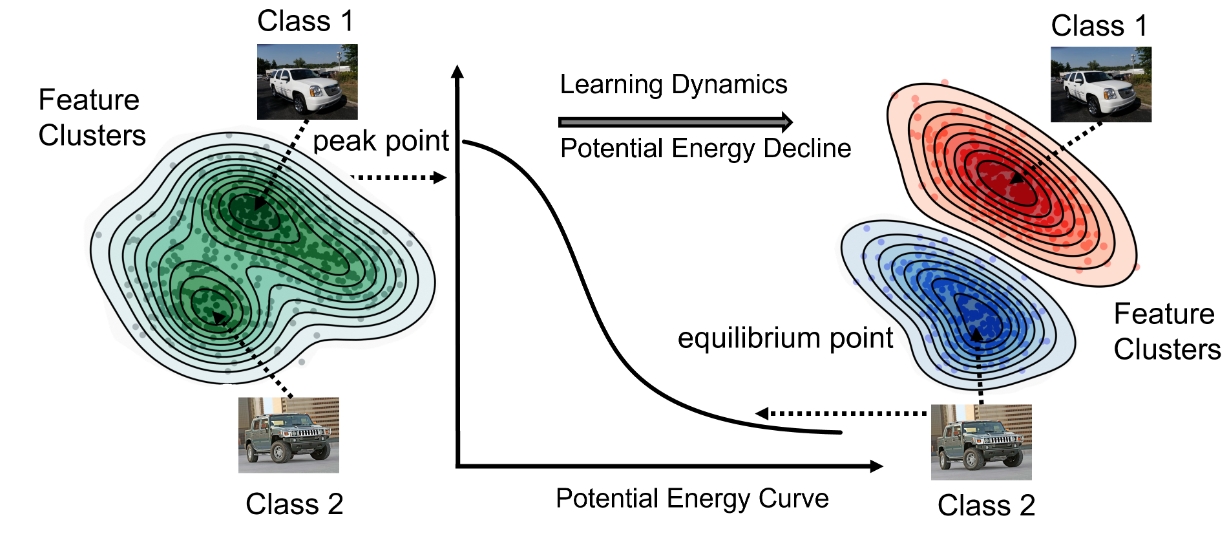
图1. 我们将迁移学习动力学从势能的角度进行类比，认为将不同类别区分开来的目标可以看作是作用在系统上的一个“力”，将系统的“势能”推向更低的方向，而动力学过程则可视为从势能平面上的不稳定点向稳定点的过程。

2. 相关工作¶

2.1 可迁移性指标¶

在计算机视觉领域，由于大规模预训练模型的应用，迁移学习已成为一个重要的里程碑。因此，从大量的模型库中选择最适合特定下游任务的模型变得非常重要，模型选择因此被提出来解决这一问题。现有的可迁移性指标方法包括:LEEP 通过估计源域和目标域的联合概率来预测标签，NLEEP 通过高斯混合模型拟合标签分布，LogME 估计给定特征的标签证据的最大值。 PARC 使用图像对之间编码特征的皮尔逊相关系数。GBC用Bhattacharyya系数测量类之间的密度分布之隔。 SFDA 在Fisher空间中测量类可区分性。这些方法对于评估监督预训练模型的可迁移性非常有效，但对于自监督学习模型仍存在挑战 ，因为这些模型本身并不足以区分不同类别的样本。

2.2 深度学习中的基于能量方法¶

基于能量的方法在机器学习领域有着悠久的历史，经常被用来模拟对象之间的相互作用。早期的工作可以追溯到受限玻尔兹曼机 (RBM)和 DeepBM，它们使用一系列的二值单元层来表示数据，并通过最小化一个能量函数来训练。 Hopfield网络也用于找到最小能量状态。 在人脸识别任务中，Uniformface和Regularface借鉴了势能中的力的概念，设计了类别间的正则化损失。受启发于这些工作，我们从潜在能量的视角重新审视迁移学习。

3. 方法¶

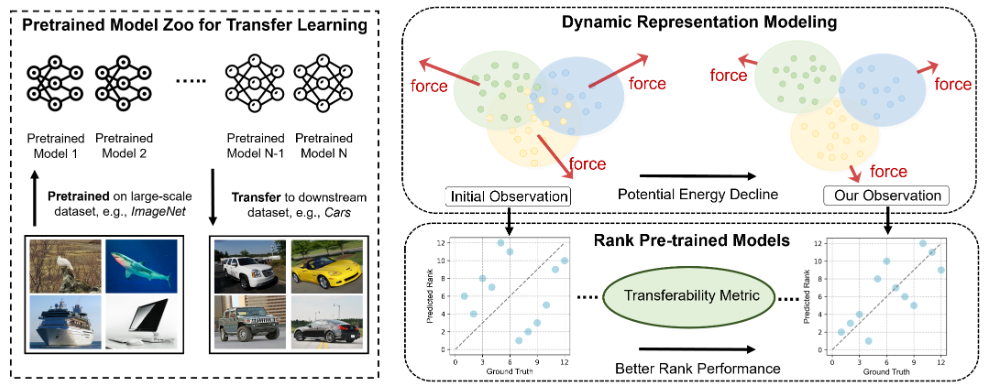
图2. 我们提出的基于势能下降(PED)的模型选择方法流程图。模型首先在大规模数据集上训练，然后转移到给定的下游任务。我们从势能的角度提出了一种新颖的方法来纠正初始观测的局限性。通过将学习动力学视为最小化势能，并考虑系统变化的趋势，我们使用基于排斥的力来模拟不同簇之间的相互作用力，以捕获移动趋势。随后，我们解冻起始状态，施加力使每个类别远离其他类别，从而降低势能。这种方法导致获得更稳定的特征观测，从而进行更准确的可迁移性得分预测。

3.1 基础知识¶

问题设置 考虑模型库 $\{Φ_i\}_{i=1}^N$，其中选择的预训练模型可以转移到下游数据集 $T = \{X， Y\}$。模型选择的目的是在不进行微调的情况下预测模型的可迁移性。

排名指标 对于模型 $Φ_i$，我们对下游数据$X$进行编码得到特征$Z$，然后将特征和标签输入指标$M(Z， Y)$来估计可迁移性得分$P_i$。直观地，该指标基于编码特征的可分性来测量可迁移性。

评估方法 我们遵循以往工作，使用加权Kendall's $τ_w$ 在预测的排名和基于微调的真实排名之间进行评估。具体而言，通过全面微调我们可以得到真实排名 $\{G_i\}_{i=1}^N$。然后$τ_w$可以表示为:

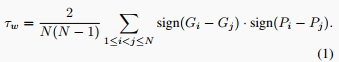
虽然现有的排名方法对于有监督的预训练模型很有效，但对于没有针对类的可分性进行训练的无监督/自监督预训练模型来说效果不佳。我们认为这主要是因为它们忽略了迁移学习微调过程中的潜在表示动力学。妥善高效地建模这样的动力学是一个关键的挑战。

3.2 从双重视角理解迁移学习¶

在这个部分，我们提供了一种新的双重视角来将基于梯度的优化重塑为物理学视角。

3.2.1 基于梯度的视角

当将预训练模型$\Phi$ parameterized by $\theta$ 转移到特定下游任务${X， Y}$时，该模型通常通过梯度反向传播来优化以最小化损失函数$L$，例如:

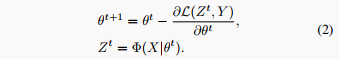
通过(2)中的迭代优化，$\Phi$区分不同类别的能力得到提升。潜在空间中不同类别的可分离性也得到增强。潜在的表示动态可以看作状态演化从$Z_{0}$到$Z_{T}$，其中$T$是迭代总数。显然，优化网络和更新其编码特征对于模型选择过程来说是非平凡的，我们需要在不进行微调的情况下模拟表示动态。

3.2.2 基于能量的视角

每一枚硬币都有两面，我们发现学习目标中的优化与物理学中的势能概念存在相似之处。直观地说，损失函数$L$和梯度$\frac{\partial L}{\partial \theta}$ 在形式上分别与势能$U$和力$F$类似，即$-\frac{\partial U}{\partial s}$。损失梯度通过调整网络参数来最小化损失和区分不同类别的特征，这与物体位置如何影响作用在它身上的力以减小势能的方式类似。基于这一洞见，我们从物理学的视角重新审视了迁移学习中的优化过程。

从物理学的视角看，在相互作用力$F$的影响下，物体运动的方向可以表示为路径$n$。随着物体在$n$路径上的运动，系统的势能会降低，如下式所示:

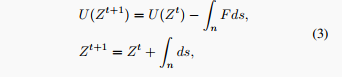
从能量角度重新思考迁移学习。基于上述发现，我们提出从潜在能量的视角重新审视迁移学习。当预训练模型收敛时，由训练目标定义的模型“系统”达到相对稳定状态，势能处于平衡。但是，当模型转移到下游任务时，由于势能景观的变化，这个初始状态变得不稳定。因此，仅根据当前观测(静态表示)预测模型的可转移性是不可靠的。

图3. 通过将问题视为最小化势能，并将每个簇视为一个球与另一个球有重叠区域(ri + rj − dij)，我们可以通过释放起始点并观察每个球在由此产生的力下被推离的方式来模拟系统的动力学。

在微调过程中，目标是将不同类别在潜在空间中区分开来，这可以看作是将簇分开的力，类似于物理学中的物体相互作用。在这种情况下，损失函数$L$基于训练样本特征$Z$的相对位置在势能面$U$上创建一个势垒，当前状态不稳定并倾向于势能下降。因此，捕获系统运动对于模型可转移性的预测至关重要。为了实现这一点，我们基于势能的概念提出了一个表示动态的物理场景。我们使用排斥力来模拟不同类别之间的相互作用，提高了学习动态的有效性和准确性。

3.3 势能驱动的动力学建模¶

我们提出了一个基于物理的建模方法PED，利用势能开发了一个机械运动过程来表示动力学。具体而言，每个类别的特征点$Z_i$在嵌入空间中被建模为高斯分布$N(c_i， σ_i^2)$，其中$c_i$是均值特征，$σ_i^2$是方差。然后将其简化为一个球，以$c_i$为其质心，$\lambda\|\sigma_i\|$为其半径$r_i$，单位质量为$m_i$。不同特征之间的排斥力被建模为球之间的弹性变形力，类似于胡克定律(即$F=kx$)。当两个球重叠时，按照连接两个球心的矢量$n$的方向施加与变形$x_e$成比例的力:

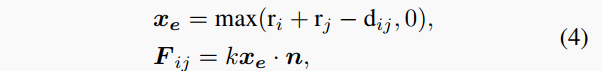
其中$k$是弹性系数， $d_{ij}$是两个球心之间的距离。如公式所示，两个簇之间的力会随着重叠越来越大而变大，当它们相离不再重叠时力为零。我们进一步对每个球建模从其他所有球所受到的合力$F_i$，并按牛顿第二运动定律求得其加速度$a_i$:

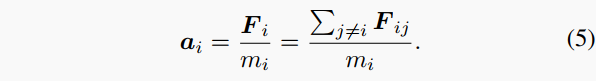
在物理学中，力通常假设在很短的时间内保持恒定。遵循这样的理念，我们提出了一种方法，通过在短时间内$\Delta t$释放系统来模拟相位位置或相对位置改变，然后使用运动方程计算位置变化:

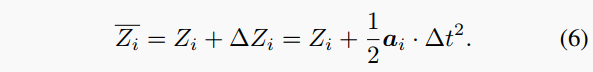
通过对系统中的样本施加力，它们会有效地朝着势能降低的方向移动。通过重复这个过程多次，我们可以获得一个势能更低的系统状态$Z$。

讨论物理建模的可行性。我们可以从另一面“硬币”的角度，即传统的基于梯度的视角来看我们的物理启发法。我们遵循胡克定律$U=\frac{1}{2}kx^2$建模系统的弹性势能，公式如下:

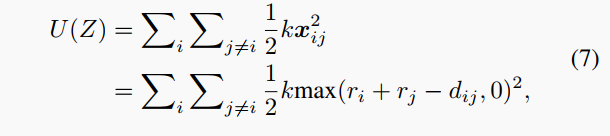
其中$x_{ij}$描述了特征簇$Z_i$和$Z_j$之间的重叠。可以看出(7)式的形式与旨在最小化不同簇重叠的基于梯度的优化方法类似，这可以看作是成对损失以提高度量学习中的类别原型分离。相比之下，我们的方法提供了一种更高效的替代优化方法，通过使用基于物理的建模方法来降低能量势垒，这可以轻松集成到现有的迁移学习方法中。

3.4 总结¶

我们的物理建模方法提供了一个新的观测$Z$来取代初始观测，而无需更新网络。动态表示是通过机械运动实现的，详细算法见算法1。任意的模型选择指标 $M(Z， Y)$ 可以用于其后排名模型，即获得$\{P_i\}_{i=1}^N$。这种方法使我们能够更好地理解系统动力学，并提升现有的模型排名算法。

算法1 基于势能衰减的算法

输入:模型库 $\{Φ_i\}_{i=1}^N$; 标注下游数据集 $T=\{X， Y\}$，包括$C$类;

超参数 $\lambda$，$\Delta t$，$k$;最大迭代步数$M$，提前终止条件$\epsilon$;

模型选择指标 $M$

输出: 每个模型的可迁移性得分 $P_i$

1 对于 $\Phi_i$ in 模型库 2 对$X$编码得到特征$Z=\Phi_i(X)$，用ImageNet特征均值$\hat{\mu}$和标准差$\hat{\sigma}$归一化:$Z\leftarrow (Z-\hat{\mu})/\hat{\sigma}$

3 当 $step \leq M$ 4 计算每个类簇$Z_j$的均值特征$c_j$和标准差$\sigma_j$

5 $c_j = E[Z_j]$， $r_j = \lambda\|\sigma_j\|$

6 计算特征簇之间的距离 $d_{jl} = \|c_j-c_l\|_2$， $j\neq l\in \{1，\cdots，C\}$

7 计算每个簇的力和加速度:

$F_j = \sum_{l≠ j} k(r_j+r_l-d_{jl})\cdot\frac{\hat{\mu}_j-\hat{\mu}_l}{\|\hat{\mu}_j-\hat{\mu}_l\|}$， $a_j = \frac{F_j}{m_j}$

8 模拟移动过程并获得更稳定的特征状态:

$z \leftarrow z + \frac{1}{2}a\Delta t^2$， $z\in Z_j$， $j\in\{1，\cdots，C\}$

9 计算终止条件:

$\omega[step] \leftarrow \|\sum_{j=1}^C \frac{1}{2}a\Delta t^2\|$

10 如果 $\omega[step]\leq \epsilon\cdot\omega[0]$: 11 跳出循环

12 $step \leftarrow step+1$

13 特征反归一化:$Z \leftarrow Z\cdot\hat{\sigma}+\hat{\mu}$

14 将$Z$和$Y$输入指标$M(Z，Y)$得到得分$P_i$

15 根据 $\{P_i\}_{i=1}^N$对模型库排序

4. 实验¶

最近年来，自监督学习作为一种主流的预训练方式，展现出比有监督学习方法更好的可迁移性。但是，潜在的学习动力学会显著影响传统的自监督模型可迁移性预测指标的性能。因此，本文分析自监督学习模型的性能来评估我们提出的方法。

表1. 在各种自监督学习模型上对不同可迁移性指标的实验结果，采用加权Kendall's τw作为排名相关性评价指标。较大的τw表示对真实排名顺序的更好预测。最好的结果以粗体表示。

下游数据集 本研究中，我们利用各种广泛使用的数据集作为下游分类任务的迁移学习，包括FGVC Aircraft、Caltech-101、Standford Cars、Cifar-10、Cifar-100、DTD、Oxford102 Flowers、Food-101和Oxford-IIIT Pets。这些数据集包括了多样性的特征，如街景、纹理、粗细分类场景，适合我们的设置。

预训练模型库 为评估我们方法对自监督学习模型的泛化性，我们考虑了12种不同类型的基于ResNet-50的预训练模型，这些模型都是使用当前状态的自监督学习方法开发的，包括BYOL、Infomin、PCLv1、PCLv2、Selav2、InsDis、SimCLRv1、SimCLRv2、MoCov1、MoCov2、DeepClusterv2和SWAV。

真实模型排名 我们实现构建模型库的真实排名$\{G_i\}_{i=1}^N$，其中使用了网格搜索策略来计算每个模型在下游任务中的真实性能。具体而言，网格搜索策略包含学习率集合$\{10^{-1}， 10^{-2}， 10^{-3}， 10^{-4}\}$和权重衰减值集合$\{10^{-6}， 10^{-5}， 10^{-4}， 10^{-3}\}$。为确保稳健性，每个实验跑了5个随机种子的平均值。从上述过程可以看出，通过微调选择最合适的模型需要大量的计算成本。

现有方法结果 我们在表1中显示了实验结果，可以看出当前最先进的方法在预测自监督模型的可迁移性上存在显著挑战，甚至在某些特定数据集上完全无法给出推荐，例如Kendall权重小于0。例如，GBC虽在有监督学习场景中通过直接测量不同簇的重叠度取得了出色的性能，但在面临不稳定的初始状态时，其预测准确性显著下降。在评估的技术中，NLEEP和SFDA由于隐式地包含了针对下游任务的适应过程，展现出较好的性能。然而，有限的初始观察仍然制约了它们的性能，例如在Aircraft上的相对低性能。上述实验结果表明，仅依赖于初始观察来预测自监督模型的性能是不可靠的，考虑表示动力学非常重要。

我们方法结果 为评估我们方法的有效性，我们将我们的方法集成到不同的最新可迁移性指标中，包括基于证据的LogME、基于可区分性的SFDA、基于分离的GBC。通过考虑动态表示，与我们方法相结合的性能在许多下游任务中显著提升。例如，与LogME和GBC相比，在Cifar100上的性能提升分别高达+0.675和+0.608。即使SFDA通过Confix特别设计了增强例来缓解微调动力学，它与我们的方法仍是正交的。例如，在Aircraft和DTD上的性能提升分别为+0.210和+0.158。尽管现有方法在表1中已经取得了显著的性能(Kendall权重上0.6以上)，但我们的方法仍可以为不同指标带来明显收益。我们的实验确认了我们基于物理的建模方法的有效性，并突出了考虑自监督模型的表示动力学的重要性。

5.可视化分析¶

5.1 不同簇的变化¶

图6的可视化揭示了自监督预训练模型编码的初始簇状态未很好地分布开来。而在迁移到下游任务时，不同的簇应该远离其他簇。因此，这凸显了我们的方法提供的改进潜力。为进一步调查基本过程，我们以BYOL模型在Cifar100数据集上为例，采用t-SNE算法可视化我们的动力学建模过程。

图4. 我们建模过程的动态特征表示的t-SNE可视化。

如图4所示，初始观察结果相当混乱，样本未按类明确分离，这是由于自监督预训练中没有类信息。因此，预测初始状态的可迁移性不可靠。然而，我们的动力学建模过程改善了特征簇的可分离性，实现了类似微调的效果，而无需网络更新。总体而言，可视化结果提供了强有力的证据来支持我们提出方法的有效性，并对促成其成功的基本过程提供了见解。

5.2 模型排名¶

通过使用我们提出的方法，我们能够优化由于初始不稳定观察而导致的相对低可迁移性分数的模型。为评估我们方法的有效性，我们生成了初始观察和我们的优化观察之间的模型排名比较可视化，如图7所示。

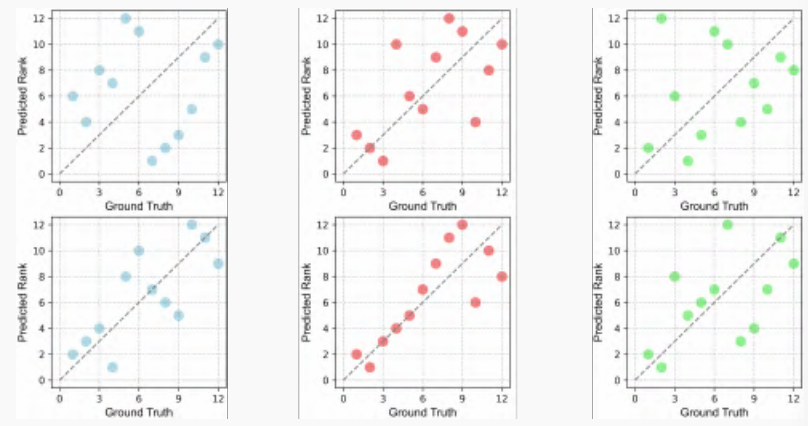
图7. 我们呈现了利用自己的观测结果和初始观测结果对可迁移性得分预测进行的模型排名变化的可视化。所描绘的过程跨越三个数据集:DTD、Flowers和Cars，从左到右安排。

结果表明，当使用我们的优化观察时，模型排名的校准获得显著改进，其中最优模型接近参考线。值得注意的是，一些起点不利的模型可以通过我们的优化方法快速提升排名，突出了我们的改进方法论的效果。

6. 效率分析¶

在实验结果中，我们已经证明了我们提出的方法在增强各种可迁移性预测技术方面的有效性。此外，我们在本节中强调我们的方法在算法复杂度和实际运行时间方面表现出计算效率。由于采用了物理学中的简化，我们的方法在计算上是高效的。具体而言，我们将同类特征建模为一个整体的球，仅考虑类中心的应力，从而导致计算复杂度为$O(C^2D)$，其中$C$表示类别数，$D$表示特征维度。因此，与可迁移性预测过程相比，我们的方法只带来相对较小的时间开销。我们在表2中呈现了我们方法在运行时间上的实验结果。显著的是，我们的方法对可迁移性预测过程贡献了最小的开销，这进一步证明了它的效果和计算效率。

表2. 在Flowers数据集上的运行时间比较。

7. 总结与展望¶

本文从一个新的视角探索了迁移学习是一种降低系统势能的过程，并提出了一种基于物理的方法来有效地模拟表征的动力学。我们的方法虽然是一种简单的物理建模，但却能一致地提升各种现有指标，提高自监督预训练模型的性能排名。在未来的工作中，我们计划通过采用自适应超参数和扩展我们的方法到更多的迁移学习场景来增加我们物理模型的复杂度。我们希望我们的工作能够激发迁移学习领域的未来研究，并产生更广泛的影响。