【GiantPandaCV导语】重新思考可变形卷积。逐行代码解析，希望读者能一起完全理解DCN并明白DCN的好处，同时也清楚DCN的缺点在哪里。最后对什么时候可以选择DCN有一个较好的认识。添加了注释的代码链接：https://github.com/BBuf/pytorch-deform-conv-v2-explain

0x00. 前言¶

之前一篇文章DCN V1代码阅读笔记已经介绍过可变形卷积这种技术，但比较可惜代码部分似乎没有解析清楚。后面，MSRA出了一篇DCNV2，也没来得及讲，因此今天这篇文章将再次回顾一下DCN V1并且讲清楚DCN V2的原理和Pytorch代码。个人是比较欣赏DCN这个工作的，我也认为卷积核不应当限制在仅仅是方形和矩形核，形状能动态变化的卷积核似乎更加符合常理，DCN的引入虽然解决了这一问题，但它的落地部署的难度也增加了，在实际部署中目前也只看到TensorRT框架有支持DCN。如果是其它前向框架想用起来DCN，难度还是比较大的。这篇文章将从各个方面深入谈一谈我眼中的DCN。

0x01. DCN V1原理回顾¶

下面的Figure2展示了可变形卷积的示意图：

Deformable Convolution的示意图

可以看到可变形卷积的结构可以分为上下两个部分，上面那部分是基于输入的特征图生成offset，而下面那部分是基于特征图和offset通过可变形卷积获得输出特征图。

假设输入的特征图宽高分别为 $w$ ， $h$ ，下面那部分的卷积核尺寸是 $k_h$ 和 $k_w$ ，那么上面那部分卷积层的卷积核数量应该是 $2\times k_h\times k_w$ ，其中 $2$ 代表 $x$ ， $y$ 两个方向的offset。

并且，这里输出特征图的维度和输入特征图的维度一样，那么offset的维度就是 $[batch, 2\times k_h\times k_w, h, w]$ ，假设下面那部分设置了group参数（代码实现中默认为 $4$ ），那么第一部分的卷积核数量就是 $2\times k_h \times k_w \times group$ ，即每一个group共用一套offset。下面的可变形卷积可以看作先基于上面那部分生成的offset做了一个插值操作，然后再执行普通的卷积。

具体实现的流程大概如下：

原始图片数据（维度是 $b*h*w*c$ ），记为U。经过一个普通卷积，填充方式为same，对应的输出结果维度是 $(b*h*w*2c)$ ，记作V。V是原始图像数据中每个像素的偏移量（因为有 $x$ 和 $y$ 两个方向，所以是 $2c$ ）。
将U中图片的像素索引值与V相加，得到偏移后的position（即在原始图片U中的坐标值），需要将position值限定为图片大小以内。position的大小为（ $b*h*w*2c$ )，但position只是一个坐标值，而且还是float类型的，我们需要这些float类型的坐标值获取像素。
举个例子，我们取一个坐标值 $(a,b)$ ，将其转换为四个整数floor(a), ceil(a), floor(b), ceil(b)，将这四个整数进行整合，得到四对坐标（floor(a),floor(b)), ((floor(a),ceil(b)), ((ceil(a),floor(b)), ((ceil(a),ceil(b))。这四对坐标每个坐标都对应U中的一个像素值，而我们需要得到(a,b)的像素值，这里采用双线性差值的方式计算（一方面是因为获得的像素更精确，另外一方面是因为可以进行反向传播）。
在得到position的所有像素后，即得到了一个新图片M，将这个新图片M作为输入数据输入到别的层中，如普通卷积。

示意图如下：

可变形卷积示意图2，来自三景页三景页博主

0x02. DCNV2?¶

我们知道DCN V1的核心公式就是：

$y(p)=\sum_{k=1}^Kw_k * x(p + p_k+\Delta_{p_k})$

CNN要学习的就是这个偏移量 $\Delta{p_k}$

然后DCN V2就在这个公式的基础上加了一项，现在变成这样子：

$y(p)=\sum_{k=1}^Kw_k * x(p + p_k+\Delta_{p_k}) * \Delta m_k$

可以看到只是在DCN V1的基础上多了一个权重项 $\Delta m_k$ ，作者说这样的好处就是增大自由度，对于某些不想要的采样点权重可以直接学习成0。

那么，比较明显DCN V1和DCN V2的代码只是多了一个系数的差别，那么代码肯定是几乎共用的，接下来我先详细解析一个DCN的Pytorch代码（包含DCN V1和DCN V2，代码链接见附录），然后谈谈DCN这个算子的优缺点以及何时选用。

0x03. 代码解析¶

直击主题，DCN的核心代码实现就是https://github.com/4uiiurz1/pytorch-deform-conv-v2/blob/master/deform_conv_v2.py这个文件了。

0x03.1 类的构造¶

# inc表示输入通道数
    # outc 表示输出通道数
    # kernel_size表示卷积核尺寸
    # stride 卷积核滑动步长
    # bias 偏置
    # modulation DCNV1还是DCNV2的开关
    def __init__(self, inc, outc, kernel_size=3, padding=1, stride=1, bias=None, modulation=False):
        """
        Args:
            modulation (bool, optional): If True, Modulated Defomable Convolution (Deformable ConvNets v2).
        """
        super(DeformConv2d, self).__init__()
        self.kernel_size = kernel_size
        self.padding = padding
        self.stride = stride
        self.zero_padding = nn.ZeroPad2d(padding)
        # 普通的卷积层，即获得了偏移量之后的特征图再接一个普通卷积
        self.conv = nn.Conv2d(inc, outc, kernel_size=kernel_size, stride=kernel_size, bias=bias)
        # 获得偏移量，卷积核的通道数应该为2xkernel_sizexkernel_size
        self.p_conv = nn.Conv2d(inc, 2*kernel_size*kernel_size, kernel_size=3, padding=1, stride=stride)
        # 偏移量初始化为0
        nn.init.constant_(self.p_conv.weight, 0)
        # 注册module反向传播的hook函数, 可以查看当前层参数的梯度
        self.p_conv.register_backward_hook(self._set_lr)
        # 将modulation赋值给当前类
        self.modulation = modulation
        if modulation:
            # 如果是DCN V2，还多了一个权重参数，用m_conv来表示
            self.m_conv = nn.Conv2d(inc, kernel_size*kernel_size, kernel_size=3, padding=1, stride=stride)
            nn.init.constant_(self.m_conv.weight, 0)
            # 注册module反向传播的hook函数, 可以查看当前层参数的梯度
            self.m_conv.register_backward_hook(self._set_lr)

    # 静态方法 类或实例均可调用，这函数的结合hook可以输出你想要的Variable的梯度
    @staticmethod
    def _set_lr(module, grad_input, grad_output):
        grad_input = (grad_input[i] * 0.1 for i in range(len(grad_input)))
        grad_output = (grad_output[i] * 0.1 for i in range(len(grad_output)))

0x03.2 _get_p函数¶

这个函数用来获取所有的卷积核偏移之后相对于原始特征图x的坐标（现在是浮点数）。

_get_p函数要求的东西实际上这个函数就需要分别求取红色块的位置，蓝色块的位置，然后再加上网络学习到的offsets获得最终的偏移坐标。

它的实现如下：

def _get_p(self, offset, dtype):
        # N = 18 / 2 = 9
        # h = 32
        # w = 32
        N, h, w = offset.size(1)//2, offset.size(2), offset.size(3)

        # (1, 2N, 1, 1)
        p_n = self._get_p_n(N, dtype)
        # (1, 2N, h, w)
        p_0 = self._get_p_0(h, w, N, dtype)
        # 卷积坐标加上之前学习出的offset后就是论文提出的公式(2)也就是加上了偏置后的卷积操作。
        # 比如p(在N=0时)p_0就是中心坐标，而p_n=(-1,-1)，所以此时的p就是卷积核中心坐标加上
        # (-1,-1)(即红色块左上方的块)再加上offset。同理可得N=1,N=2...分别代表了一个卷积核
        # 上各个元素。
        p = p_0 + p_n + offset
        return p

里面的_get_p_n函数是用来生成卷积的相对坐标，其中卷积的中心点被看成原点，然后其它点的坐标都是相对于原点来说的，例如self.kernel_size=3，通过torch.meshgrid生成从（-1，-1）到（1，1）9个坐标。将坐标的x和y分别存储，然后再将x，y以(1,2N,1,1)的形式返回，这样我们就获取了一个卷积核的所有相对坐标。

然后，_get_p_0是获取卷积核在特征图上对应的中心坐标，也即论文公式中的p_0，通过torch.mershgrid生成所有的中心坐标，然后通过kernel_size推断初始坐标，然后通过stride推断所有的中心坐标，这里注意一下，代码默认torch.arange从1开始，实际上这是kernel_size为3时的情况，严谨一点torch.arange应该从kernel_size//2开始，因此下面这个实现只适合3x3的卷积。代码实现如下：

def _get_p_0(self, h, w, N, dtype):
        # 设w = 7, h = 5, stride = 1
        # 有p_0_x = tensor([[1, 1, 1, 1, 1, 1, 1],
        # [2, 2, 2, 2, 2, 2, 2],
        # [3, 3, 3, 3, 3, 3, 3],
        # [4, 4, 4, 4, 4, 4, 4],
        # [5, 5, 5, 5, 5, 5, 5]])
        # p_0_x.shape = [5, 7]
        # p_0_y = tensor([[1, 2, 3, 4, 5, 6, 7],
        # [1, 2, 3, 4, 5, 6, 7],
        # [1, 2, 3, 4, 5, 6, 7],
        # [1, 2, 3, 4, 5, 6, 7],
        # [1, 2, 3, 4, 5, 6, 7]])
        # p_0_y.shape = [5, 7]
        p_0_x, p_0_y = torch.meshgrid(
            torch.arange(1, h*self.stride+1, self.stride),
            torch.arange(1, w*self.stride+1, self.stride))
        # p_0_x的shape为torch.Size([1, 9, 5, 7])
        p_0_x = torch.flatten(p_0_x).view(1, 1, h, w).repeat(1, N, 1, 1)
        # p_0_y的shape为torch.Size([1, 9, 5, 7])
        p_0_y = torch.flatten(p_0_y).view(1, 1, h, w).repeat(1, N, 1, 1)
        # p_0的shape为torch.Size([1, 18, 5, 7])
        p_0 = torch.cat([p_0_x, p_0_y], 1).type(dtype)

        return p_0

0x03.3 forward函数¶

为了便于理解这部分代码，再放一张DCN比较形象的图例：

DCN示意图这部分的详细代码解释如下：

# 前向传播函数
    def forward(self, x):
        # 获得输入特征图x的偏移量
        # 假设输入特征图shape是[1,3,32,32]，然后卷积核是3x3，
        # 输出通道数为32，那么offset的shape是[1,2*3*3,32]
        offset = self.p_conv(x)
        # 如果是DCN V2那么还需要获得输入特征图x偏移量的权重项
        # 假设输入特征图shape是[1,3,32,32]，然后卷积核是3x3，
        # 输出通道数为32，那么offset的权重shape是[1,3*3,32]
        if self.modulation:
            m = torch.sigmoid(self.m_conv(x))
        # dtype = torch.float32
        dtype = offset.data.type()
        # 卷积核尺寸大小
        ks = self.kernel_size
        # N=2*3*3/2=3*3=9
        N = offset.size(1) // 2
        # 如果需要Padding就先Padding
        if self.padding:
            x = self.zero_padding(x)

        # p的shape为(b, 2N, h, w)
        # 这个函数用来获取所有的卷积核偏移之后相对于原始特征图x的坐标（现在是浮点数）
        p = self._get_p(offset, dtype)

        # 我们学习出的量是float类型的，而像素坐标都是整数类型的，
        # 所以我们还要用双线性插值的方法去推算相应的值
        # 维度转换，现在p的维度为(b, h, w, 2N)
        p = p.contiguous().permute(0, 2, 3, 1)
        # floor是向下取整
        q_lt = p.detach().floor()
        # +1相当于原始坐标向上取整
        q_rb = q_lt + 1
        # 将q_lt即左上角坐标的值限制在图像范围内
        q_lt = torch.cat([torch.clamp(q_lt[..., :N], 0, x.size(2)-1), torch.clamp(q_lt[..., N:], 0, x.size(3)-1)], dim=-1).long()
        # 将q_rb即右下角坐标的值限制在图像范围内
        q_rb = torch.cat([torch.clamp(q_rb[..., :N], 0, x.size(2)-1), torch.clamp(q_rb[..., N:], 0, x.size(3)-1)], dim=-1).long()
        # 用q_lt的前半部分坐标q_lt_x和q_rb的后半部分q_rb_y组合成q_lb
        q_lb = torch.cat([q_lt[..., :N], q_rb[..., N:]], dim=-1)
        # 同理
        q_rt = torch.cat([q_rb[..., :N], q_lt[..., N:]], dim=-1)

        # 对p的坐标也要限制在图像范围内
        p = torch.cat([torch.clamp(p[..., :N], 0, x.size(2)-1), torch.clamp(p[..., N:], 0, x.size(3)-1)], dim=-1)

        # bilinear kernel (b, h, w, N)
        # 双线性插值的4个系数
        g_lt = (1 + (q_lt[..., :N].type_as(p) - p[..., :N])) * (1 + (q_lt[..., N:].type_as(p) - p[..., N:]))
        g_rb = (1 - (q_rb[..., :N].type_as(p) - p[..., :N])) * (1 - (q_rb[..., N:].type_as(p) - p[..., N:]))
        g_lb = (1 + (q_lb[..., :N].type_as(p) - p[..., :N])) * (1 - (q_lb[..., N:].type_as(p) - p[..., N:]))
        g_rt = (1 - (q_rt[..., :N].type_as(p) - p[..., :N])) * (1 + (q_rt[..., N:].type_as(p) - p[..., N:]))

        # (b, c, h, w, N)
        # 现在只获取了坐标值，我们最终木的是获取相应坐标上的值，
        # 这里我们通过self._get_x_q()获取相应值。
        x_q_lt = self._get_x_q(x, q_lt, N)
        x_q_rb = self._get_x_q(x, q_rb, N)
        x_q_lb = self._get_x_q(x, q_lb, N)
        x_q_rt = self._get_x_q(x, q_rt, N)

        # (b, c, h, w, N)
        # 双线性插值计算
        x_offset = g_lt.unsqueeze(dim=1) * x_q_lt + \
                   g_rb.unsqueeze(dim=1) * x_q_rb + \
                   g_lb.unsqueeze(dim=1) * x_q_lb + \
                   g_rt.unsqueeze(dim=1) * x_q_rt

        # modulation
        if self.modulation:
            m = m.contiguous().permute(0, 2, 3, 1)
            m = m.unsqueeze(dim=1)
            m = torch.cat([m for _ in range(x_offset.size(1))], dim=1)
            x_offset *= m

        # 在获取所有值后我们计算出x_offset，但是x_offset的size
        # 是(b,c,h,w,N)，我们的目的是将最终的输出结果的size变
        # 成和x一致即(b,c,h,w)，所以在最后用了一个reshape的操作。
        # 这里ks=3
        x_offset = self._reshape_x_offset(x_offset, ks)
        out = self.conv(x_offset)

        return out

关于插值的系数计算解释如下：

假设原始图像的大小是 $m\times n$ ，目标图像是 $a\times b$ ，那么两幅图像的边长比分别是 $m/a$ 和 $n/b$ 。那么目标图像的 $(i,j)$ 位置的像素可以通过上面的比例对应回原图像，坐标为 $(i*m/a,j*n/b)$ 。当然这样获得的坐标可能不是整数，如果强行取整就是普通的线性插值，而双线性插值就是通过寻找距离这个对应坐标最近的四个像素点，来计算该点的值，如果坐标是 $(2.5,4.5)$ ，那么最近的四个像素是 $(2，4),(2，5), <span><span class="MathJax_Preview">(3，4)</span><script type="math/tex">(3，4)$ ，，(3，5) $。如果图形是灰度图，那么$ (i,j) $点的像素值可以通过下面的公式计算： <span><span class="MathJax_Preview">f(i, j)=w1*p1+w2*p2+w3*p3+w4*p4</span><script type="math/tex">f(i, j)=w1*p1+w2*p2+w3*p3+w4*p4$ 其中，其中，pi=(1,2,3,4) $为最近的$ 4 $个像素点，$ w_i$为各点的权重。

到这里并没有结束，我们需要特别注意的是，仅仅按照上面得到公式实现的双线性插值的结果和OpenCV/Matlab的结果是对应不起来的，这是为什么呢？

原因就是因为坐标系的选取问题，按照一些网上的公开实现，将源图像和目标图像的原点均选在左上角，然后根据插值公式计算目标图像每个点的像素，假设我们要将 $5\times 5$ 的图像缩小成 $3\times 3$ ，那么源图像和目标图像的对应关系如下图所示：

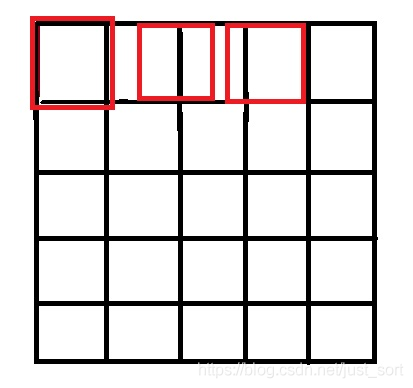
按照网上大多数公开的源码实现的像素对应关系

可以看到如果选择了左上角作为原点，那么最右边和最下边的像素是没有参与计算的，所以我们得到的结果和OpenCV/MatLab中的结果不会一致，那应该怎么做才是对的呢？

答案就是让两个图像的几何中心重合，并且目标图像的每个像素之间都是等间隔的，并且都和两边有一定的边距。如下图所示：

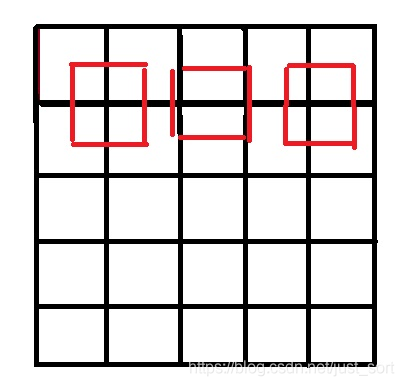
让两个图像的几何中心重合后的像素对应关系

所以，我们只需要在计算坐标的时候将：

int x=i*m/a;
int y=j*n/b;

改成：

int x=(i+0.5)*m/a-0.5;
int y=(j+0.5)*n/b-0.5;

即可获得正确的双线性插值结果，一份c++代码实现如下：

https://github.com/BBuf/Image-processing-algorithm/blob/master/Image%20Interpolation/BilinearInterpolation.cpp

Mat BilinearInterpolation(Mat src, float sx, float sy) {
    int row = src.rows;
    int col = src.cols;
    int channels = src.channels();
    int dst_row = round(row * sx);
    int dst_col = round(col * sy);
    Mat dst(dst_row, dst_col, CV_8UC3);
    for (int i = 0; i < dst_row; i++) {
        int index_i = (i + 0.5) / sx - 0.5;
        if (index_i < 0) index_i = 0;
        if (index_i > row - 2) index_i = row - 2;
        int i1 = floor(index_i);
        int i2 = ceil(index_i);
        float u = index_i - i1;
        for (int j = 0; j < dst_col; j++) {
            float index_j = (j + 0.5) / sy - 0.5;
            if (index_j < 0) index_j = 0;
            if (index_j > col - 2) index_j = col - 2;
            int j1 = floor(index_j);
            int j2 = ceil(index_j);
            float v = index_j - j1;
            for (int k = 0; k < 3; k++) {
                dst.at<cv::Vec3b>(i, j)[k] = (1 - u)*(1 - v)*src.at<cv::Vec3b>(i1, j1)[k] + 
                    (1 - u)*v*src.at<cv::Vec3b>(i1, j2)[k] + u*(1 - v)*src.at<cv::Vec3b>(i2, j1)[k] + u*v*src.at<cv::Vec3b>(i2, j2)[k];
            }
        }
    }
    return dst;
}

可以看到插值的4个系数和forward中的：

# 双线性插值的4个系数
g_lt = (1 + (q_lt[..., :N].type_as(p) - p[..., :N])) * (1 + (q_lt[..., N:].type_as(p) - p[..., N:]))
 g_rb = (1 - (q_rb[..., :N].type_as(p) - p[..., :N])) * (1 - (q_rb[..., N:].type_as(p) - p[..., N:]))
 g_lb = (1 + (q_lb[..., :N].type_as(p) - p[..., :N])) * (1 - (q_lb[..., N:].type_as(p) - p[..., N:]))
 g_rt = (1 - (q_rt[..., :N].type_as(p) - p[..., :N])) * (1 + (q_rt[..., N:].type_as(p) - p[..., N:]))

一一对应。

0x03.4 _reshape_x_offset函数¶

还需要特别注意一下这个函数：

def _reshape_x_offset(x_offset, ks):
        # 函数首先获取了x_offset的所有size信息，然后以kernel_size为
        # 单位进行reshape，因为N=kernel_size*kernel_size，所以我们
        # 分两次进行reshape，第一次先把输入view成(b,c,h,ks*w,ks)，
        # 第二次再view将size变成(b,c,h*ks,w*ks)

        b, c, h, w, N = x_offset.size()
        x_offset = torch.cat([x_offset[..., s:s+ks].contiguous().view(b, c, h, w*ks) for s in range(0, N, ks)], dim=-1)
        x_offset = x_offset.contiguous().view(b, c, h*ks, w*ks)

        return x_offset

这个地方感觉需要这样来想：

我们知道我们获得的偏移坐标x_offsets在没有reshape之前的维度是 $[b,c,h,w,N]$ ，其中 $N=k_s*k_s$ 表示卷积核上的各个元素。然后这里的reshape操作就是把这些元素放到二维空间上，类似于GEMM算法。如下图：

来自知乎：https://zhuanlan.zhihu.com/p/102707081，表示_reshape_x_offset函数中Reshape的真实意义

可以看到，这里的 $3\times 3$ 卷积每次涉及到9个元素的运算，然后右边的图是把每次卷积操作时的元素都保存下来，其中 $N=k_s*k_s$ 。

至此，我们就对输入数据 $x$ 完成了可变形卷积，然后每次把卷积所需要的数据单独作为一个小块保留，最终获得了一张很大的特征图，维度是 $(b,c,ks*h,ks*w)$ ，这个时候大特征图的每个 $k_s*k_s$ 小块就是论文中的 $x(p_0+p_n+\Delta p_n)$ 了，当然如果是DCN V2就多乘一个权重系数就好了。

最后再经过一个普通的以 $k_s$ 为stride的卷积层，所有的操作就等价于论文列出的可变形卷积公式了呀！也即：

$y(p)=\sum_{k=1}^Kw_k * x(p + p_k+\Delta_{p_k})$

0x04. 致命缺点¶

上面那俩个Reshape操作虽然实现了可变形卷积到正常卷积的过渡，但是这种做法有一个致命缺点，那就是卷积核一旦很大，那么整个算法会消耗掉非常大的空间。因为最终的大特征图是 $[bs,c,ks*h,ks*w]$ 啊。

这个问题怎么解决呢？我也不太清楚，需要研究一下作者的Cuda代码，这个留到以后说吧。

另外，在部署落地的时候更多应当考虑OP的通用性，以及这个OP相对于普通的卷积带来的精度提升是否值得为其单独做一套部署方案。我们可以发现DCN这个操作相关的Pytorch操作实在是太多了，虽然各个前向推理框架都支持里面的任意一种操作，但仍需要花较多精力去拼出这个OP，同时还要应对各种精度下降的问题。

去搜索了一下，目前只有TensorRT支持了DCN的部署，其它部署框架似乎都没有支持（也有可能我信息获取有误，如果有支持的可以告诉我）。因此如果你要用DCN落地业务请慎重哦。

不过DCN的特性和性能提升摆在这里，比赛可以用起来啊！

0x05. 小结¶

这篇文章更加详细的思考了DCN V1/V2，并进行了逐行代码分析，如果看完这篇文章还有没有理解的地方可以评论区讨论呀。后面可能会再更新一篇DCN的C++工程实现哦，或许哪位大佬能试试将DCN在其它框架比如NCNN上部署一下？（~~等着白嫖了~~ ）

0x06. 参考¶

本文总阅读量次