1. 前言¶

笔者前几天阅读了MASA 的可变形卷积算法，并写了一篇算法笔记：MASA DCN(可变形卷积) 算法笔记，然后里面也说了会放出一个代码解读出来，所以今天的推文就是来干这件事的，希望看完这篇文章你可对DCN的细节可以更加了解。本次解析的代码来自：https://github.com/ChunhuanLin/deform_conv_pytorch 。

2. 代码整体介绍¶

打开这个工程，我们发现只有 $3$ 个文件，整个结构非常简单：

代码结构

实际上我们关注前面 $2$ 个文件deform_conv.py和demo.py就可以了，至于test_against_mxnet.ipynb只是测试了以下mxnet自带的可变形卷积op和这个库里面实现的可变形卷积op对同一个输入进行处理，输出结果是否一致，从jupyter的结果来看是完全一致的，也证明作者这个DeformConv2D是正确实现了，接下来我们就从源码角度来看一下可变形卷积究竟是如何实现的。

另外需要注意的是这个Pytorch代码版本是0.4.1，如果需要使用1.0以上的可能需要稍微改改某些API，但改动应该很少的，毕竟这个代码加起来也就2,300行。。

3. 可变形卷积示意图¶

为了更好的理解代码，我们先形象的回忆一下可变形卷积。

下面的Figure2展示了可变形卷积的示意图：

Deformable Convolution的示意图

可以看到可变形卷积的结构可以分为上下两个部分，上面那部分是基于输入的特征图生成offset，而下面那部分是基于特征图和offset通过可变形卷积获得输出特征图。

假设输入的特征图宽高分别为 $w$ ， $h$ ，下面那部分的卷积核尺寸是 $k_h$ 和 $k_w$ ，那么上面那部分卷积层的卷积核数量应该是 $2\times k_h\times k_w$ ，其中 $2$ 代表 $x$ ， $y$ 两个方向的offset。

并且，这里输出特征图的维度和输入特征图的维度一样，那么offset的维度就是 $[batch, 2\times k_h\times k_w, h, w]$ ，假设下面那部分设置了group参数（代码实现中默认为 $4$ ），那么第一部分的卷积核数量就是 $2\times k_h \times k_w \times group$ ，即每一个group共用一套offset。下面的可变形卷积可以看作先基于上面那部分生成的offset做了一个插值操作，然后再执行普通的卷积。

4. 解析`demo.py`¶

demo.py是训练和参数设置的入口，我们进来看看。

首先是设置一些训练参数，并加载MNIST数据集到train_loader和test_loader里面：

# Training settings
parser = argparse.ArgumentParser(description='PyTorch MNIST Example')
# 设置训练batch_size，默认为32
parser.add_argument('--batch-size', type=int, default=32, metavar='N',
                    help='input batch size for training (default: 32)')
# 设置测试的batch_size，默认为32
parser.add_argument('--test-batch-size', type=int, default=32, metavar='N',
                    help='input batch size for testing (default: 32)')
# 设置训练epochs数，默认为10
parser.add_argument('--epochs', type=int, default=10, metavar='N',
                    help='number of epochs to train (default: 10)')
# 设置学习率，默认为0.01
parser.add_argument('--lr', type=float, default=0.01, metavar='LR',
                    help='learning rate (default: 0.01)')
# 设置SGD的动量参数，默认为0.5
parser.add_argument('--momentum', type=float, default=0.5, metavar='M',
                    help='SGD momentum (default: 0.5)')
# 设置是否使用GPU训练
parser.add_argument('--no-cuda', action='store_true', default=False,
                    help='disables CUDA training')
# 设置随机数种子
parser.add_argument('--seed', type=int, default=1, metavar='S',
                    help='random seed (default: 1)')
# 没用到这个参数，不用管
parser.add_argument('--log-interval', type=int, default=10, metavar='N',
                    help='how many batches to wait before logging training status')

# 解析参数
args = parser.parse_args()
args.cuda = not args.no_cuda and torch.cuda.is_available()

torch.manual_seed(args.seed)
if args.cuda:
    # 为当前GPU设置随机种子
    # 如果使用多个GPU，应该使用torch.cuda.manual_seed_all()为所有的GPU设置种子
    torch.cuda.manual_seed(args.seed)

kwargs = {'num_workers': 1, 'pin_memory': True} if args.cuda else {}

# 加载数据。组合数据集和采样器，提供数据上的单或多进程迭代器
# 参数：
# dataset：Dataset类型，从其中加载数据
# batch_size：int，可选。每个batch加载多少样本
# shuffle：bool，可选。为True时表示每个epoch都对数据进行洗牌
# sampler：Sampler，可选。从数据集中采样样本的方法。
# num_workers：int，可选。加载数据时使用多少子进程。默认值为0，表示在主进程中加载数据。
# collate_fn：callable，可选。
# pin_memory：bool，可选
# drop_last：bool，可选。True表示如果最后剩下不完全的batch,丢弃。False表示不丢弃。

train_loader = torch.utils.data.DataLoader(
    datasets.MNIST('./MNIST', train=True, download=True,
                   transform=transforms.Compose([
                       transforms.ToTensor(),
                       transforms.Normalize((0.1307,), (0.3081,))
                   ])),
    batch_size=args.batch_size, shuffle=True, **kwargs)
test_loader = torch.utils.data.DataLoader(
    datasets.MNIST('./MNIST', train=False, download=True,
                   transform=transforms.Compose([
                       transforms.ToTensor(),
                       transforms.Normalize((0.1307,), (0.3081,))
                   ])),
    batch_size=args.test_batch_size, shuffle=True, **kwargs)

接下来开始构造一个DCN，代码如下：

# 构造一个DeformNet，只把其中一个卷积层改成了DeformConv2d
class DeformNet(nn.Module):
    def __init__(self):
        super(DeformNet, self).__init__()
        self.conv1 = nn.Conv2d(1, 32, kernel_size=3, padding=1)
        self.bn1 = nn.BatchNorm2d(32)

        self.conv2 = nn.Conv2d(32, 64, kernel_size=3, padding=1)
        self.bn2 = nn.BatchNorm2d(64)

        self.conv3 = nn.Conv2d(64, 128, kernel_size=3, padding=1)
        self.bn3 = nn.BatchNorm2d(128)

        self.offsets = nn.Conv2d(128, 18, kernel_size=3, padding=1)
        self.conv4 = DeformConv2D(128, 128, kernel_size=3, padding=1)
        self.bn4 = nn.BatchNorm2d(128)

        self.classifier = nn.Linear(128, 10)

    def forward(self, x):
        # convs
        x = F.relu(self.conv1(x))
        x = self.bn1(x)
        x = F.relu(self.conv2(x))
        x = self.bn2(x)
        x = F.relu(self.conv3(x))
        x = self.bn3(x)
        # deformable convolution
        offsets = self.offsets(x)
        x = F.relu(self.conv4(x, offsets))
        x = self.bn4(x)

        x = F.avg_pool2d(x, kernel_size=28, stride=1).view(x.size(0), -1)
        x = self.classifier(x)
        # Pytorch为什么用log_softmax，因为后面损失函数用的nll_loss
        return F.log_softmax(x, dim=1)

再接下来就是权重，offsets初始化以及训练测试了，没啥好说的，看下代码吧：

model = DeformNet()

# 初始化权重
def init_weights(m):
    if isinstance(m, nn.Conv2d) or isinstance(m, nn.Linear):
        nn.init.xavier_uniform(m.weight, gain=nn.init.calculate_gain('relu'))
        if m.bias is not None:
            m.bias.data = torch.FloatTensor(m.bias.shape[0]).zero_()

# 初始化偏移
def init_conv_offset(m):
    m.weight.data = torch.zeros_like(m.weight.data)
    if m.bias is not None:
        m.bias.data = torch.FloatTensor(m.bias.shape[0]).zero_()


model.apply(init_weights)
model.offsets.apply(init_conv_offset)

if args.cuda:
    model.cuda()

optimizer = optim.SGD(model.parameters(), lr=args.lr, momentum=args.momentum)


def train(epoch):
    # 把module设成training模式，对Dropout和BatchNorm有影响
    model.train()
    for batch_idx, (data, target) in enumerate(train_loader):
         '''
        Variable类对Tensor对象进行封装，会保存该张量对应的梯度，以及对生成该张量的函数grad_fn的一个引用。
        如果该张量是用户创建的，grad_fn是None，称这样的Variable为叶子Variable。
        '''
        data, target = Variable(data), Variable(target)
        if args.cuda:
            data, target = data.cuda(), target.cuda()
        optimizer.zero_grad()
        output = model(data)
        # 负log似然损失
        loss = F.nll_loss(output, target)
        loss.backward()
        optimizer.step()
        if batch_idx % args.log_interval == 0:
            print('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}'.format(
                epoch, batch_idx * len(data), len(train_loader.dataset),
                100. * batch_idx / len(train_loader), loss.data[0]))

def test():
     # 把module设置为评估模式，只对Dropout和BatchNorm模块有影响
    model.eval()
    test_loss = 0
    correct = 0
    for data, target in test_loader:
        if args.cuda:
            data, target = data.cuda(), target.cuda()
        data, target = Variable(data, volatile=True), Variable(target)
        output = model(data)
        test_loss += F.nll_loss(output, target, size_average=False).data[0] # sum up batch loss
        pred = output.data.max(1, keepdim=True)[1] # get the index of the max log-probability
        correct += pred.eq(target.data.view_as(pred)).cpu().sum()

    test_loss /= len(test_loader.dataset)
    print('\nTest set: Average loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)\n'.format(
        test_loss, correct, len(test_loader.dataset),
        100. * correct / len(test_loader.dataset)))

# 执行训练，每个epoch都进行测试
for epoch in range(1, args.epochs + 1):
    since = time()
    train(epoch)
    iter = time() - since
    print("Spends {}s for each training epoch".format(iter/args.epochs))
    test()

5. 解析`deform_conv.py`¶

上面的代码解析只是讲了个网络的外包装，真正的可变形卷积的代码实现在deform_conv.py里面，可变形卷积的具体流程是：

原始图片数据（维度是 $b*h*w*c$ ），记为U。经过一个普通卷积，填充方式为same，对应的输出结果维度是 $(b*h*w*2c)$ ，记作V。V是原始图像数据中每个像素的偏移量（因为有 $x$ 和 $y$ 两个方向，所以是 $2c$ ）。
将U中图片的像素索引值与V相加，得到偏移后的position（即在原始图片U中的坐标值），需要将position值限定为图片大小以内。position的大小为（ $b*h*w*2c$ )，但position只是一个坐标值，而且还是float类型的，我们需要这些float类型的坐标值获取像素。
举个例子，我们取一个坐标值 $(a,b)$ ，将其转换为四个整数floor(a), ceil(a), floor(b), ceil(b)，将这四个整数进行整合，得到四对坐标（floor(a),floor(b)), ((floor(a),ceil(b)), ((ceil(a),floor(b)), ((ceil(a),ceil(b))。这四对坐标每个坐标都对应U中的一个像素值，而我们需要得到(a,b)的像素值，这里采用双线性差值的方式计算（一方面是因为获得的像素更精确，另外一方面是因为可以进行反向传播）。
在得到position的所有像素后，即得到了一个新图片M，将这个新图片M作为输入数据输入到别的层中，如普通卷积。

示意图如下：

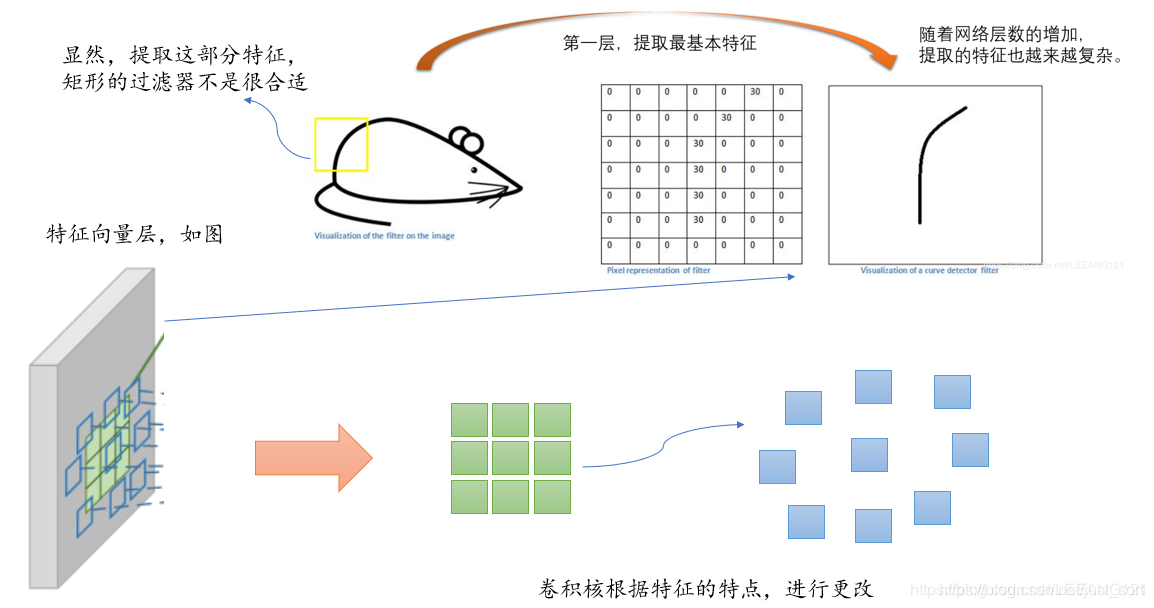
可变形卷积实现的示意图1，来自三景页三景页博主

可变形卷积示意图2，来自三景页三景页博主

然后想说的是，这份代码应该是我找到的实现最简单的代码了，但我看完仍然只能直呼其内行，这个代码十分难以理解，在理解这个代码之前必须先清楚双线性插值的原理，接下来我们先来说说双线性插值。

5.1 双线性插值¶

假设原始图像的大小是 $m\times n$ ，目标图像是 $a\times b$ ，那么两幅图像的边长比分别是 $m/a$ 和 $n/b$ 。那么目标图像的 $(i,j)$ 位置的像素可以通过上面的比例对应回原图像，坐标为 $(i*m/a,j*n/b)$ 。当然这样获得的坐标可能不是整数，如果强行取整就是普通的线性插值，而双线性插值就是通过寻找距离这个对应坐标最近的四个像素点，来计算该点的值，如果坐标是 $(2.5,4.5)$ ，那么最近的四个像素是 $(2，4),(2，5), <span><span class="MathJax_Preview">(3，4)</span><script type="math/tex">(3，4)$ ，，(3，5) $。如果图形是灰度图，那么$ (i,j)$点的像素值可以通过下面的公式计算：

$f(i, j)=w1*p1+w2*p2+w3*p3+w4*p4$

其中， $pi=(1,2,3,4)$ 为最近的 $4$ 个像素点， $w_i$ 为各点的权重。

到这里并没有结束，我们需要特别注意的是，仅仅按照上面得到公式实现的双线性插值的结果和OpenCV/Matlab的结果是对应不起来的，这是为什么呢？

原因就是因为坐标系的选取问题，按照一些网上的公开实现，将源图像和目标图像的原点均选在左上角，然后根据插值公式计算目标图像每个点的像素，假设我们要将 $5\times 5$ 的图像缩小成 $3\times 3$ ，那么源图像和目标图像的对应关系如下图所示：

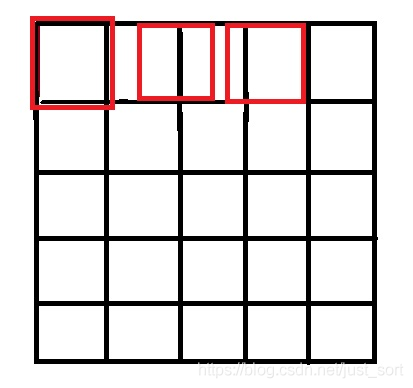
按照网上大多数公开的源码实现的像素对应关系

可以看到如果选择了左上角作为原点，那么最右边和最下边的像素是没有参与计算的，所以我们得到的结果和OpenCV/MatLab中的结果不会一致，那应该怎么做才是对的呢？

答案就是让两个图像的几何中心重合，并且目标图像的每个像素之间都是等间隔的，并且都和两边有一定的边距。如下图所示：

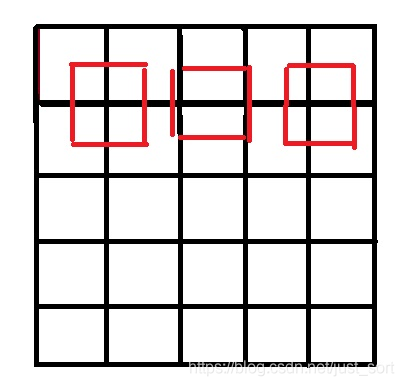
让两个图像的几何中心重合后的像素对应关系

所以，我们只需要在计算坐标的时候将：

int x=i*m/a;
int y=j*n/b;

改成：

int x=(i+0.5)*m/a-0.5;
int y=(j+0.5)*n/b-0.5;

即可获得正确的双线性插值结果，代码实现如下：

https://github.com/BBuf/Image-processing-algorithm/blob/master/Image%20Interpolation/BilinearInterpolation.cpp

Mat BilinearInterpolation(Mat src, float sx, float sy) {
    int row = src.rows;
    int col = src.cols;
    int channels = src.channels();
    int dst_row = round(row * sx);
    int dst_col = round(col * sy);
    Mat dst(dst_row, dst_col, CV_8UC3);
    for (int i = 0; i < dst_row; i++) {
        int index_i = (i + 0.5) / sx - 0.5;
        if (index_i < 0) index_i = 0;
        if (index_i > row - 2) index_i = row - 2;
        int i1 = floor(index_i);
        int i2 = ceil(index_i);
        float u = index_i - i1;
        for (int j = 0; j < dst_col; j++) {
            float index_j = (j + 0.5) / sy - 0.5;
            if (index_j < 0) index_j = 0;
            if (index_j > col - 2) index_j = col - 2;
            int j1 = floor(index_j);
            int j2 = ceil(index_j);
            float v = index_j - j1;
            for (int k = 0; k < 3; k++) {
                dst.at<cv::Vec3b>(i, j)[k] = (1 - u)*(1 - v)*src.at<cv::Vec3b>(i1, j1)[k] + 
                    (1 - u)*v*src.at<cv::Vec3b>(i1, j2)[k] + u*(1 - v)*src.at<cv::Vec3b>(i2, j1)[k] + u*v*src.at<cv::Vec3b>(i2, j2)[k];
            }
        }
    }
    return dst;
}

5.2 可变形卷积实现¶

有了上面的铺垫大概就知道可变形卷积每一步大概是在干什么了，代码解析如下：

class DeformConv2D(nn.Module):
    def __init__(self, inc, outc, kernel_size=3, padding=1, bias=None):
        super(DeformConv2D, self).__init__()
        self.kernel_size = kernel_size
        self.padding = padding
        self.zero_padding = nn.ZeroPad2d(padding)
        self.conv_kernel = nn.Conv2d(inc, outc, kernel_size=kernel_size, stride=kernel_size, bias=bias)

    # 注意，offset的Tensor尺寸是[b, 18, 3, 3]
    def forward(self, x, offset):
        dtype = offset.data.type()
        ks = self.kernel_size
        # N=9=3x3
        N = offset.size(1) // 2

        # 将offset的顺序从[x1, y1, x2, y2, ...] 改成[x1, x2..., y1, y2, ...]
        offsets_index = Variable(torch.cat([torch.arange(0, 2*N, 2), torch.arange(1, 2*N+1, 2)]), requires_grad=False).type_as(x).long()
        # torch.unsqueeze()是为了增加维度
        offsets_index = offsets_index.unsqueeze(dim=0).unsqueeze(dim=-1).unsqueeze(dim=-1).expand(*offset.size())
        # 根据维度dim按照索引列表index从offset中选取指定元素
        offset = torch.gather(offset, dim=1, index=offsets_index)
        # ------------------------------------------------------------------------

        # 对输入x进行padding
        if self.padding:
            x = self.zero_padding(x)

        # 将offset放到网格上，也即是图中所示的那个绿色带箭头的offset图
        # (b, 2N, h, w)
        p = self._get_p(offset, dtype)

        # 维度变换
        # (b, h, w, 2N)
        p = p.contiguous().permute(0, 2, 3, 1)
        # floor是向下取整
        q_lt = Variable(p.data, requires_grad=False).floor()
        # +1相当于向上取整
        q_rb = q_lt + 1

        # 将lt限制在图像范围内
        q_lt = torch.cat([torch.clamp(q_lt[..., :N], 0, x.size(2)-1), torch.clamp(q_lt[..., N:], 0, x.size(3)-1)], dim=-1).long()
        # 将rb限制在图像范围内
        q_rb = torch.cat([torch.clamp(q_rb[..., :N], 0, x.size(2)-1), torch.clamp(q_rb[..., N:], 0, x.size(3)-1)], dim=-1).long()
        # 获得lb
        q_lb = torch.cat([q_lt[..., :N], q_rb[..., N:]], -1)
        # 获得rt
        q_rt = torch.cat([q_rb[..., :N], q_lt[..., N:]], -1)

        # 插值的时候需要考虑一下padding对原始索引的影响
        # (b, h, w, N)
        # torch.lt() 逐元素比较input和other，即是否input < other
        # torch.rt() 逐元素比较input和other，即是否input > other
        mask = torch.cat([p[..., :N].lt(self.padding)+p[..., :N].gt(x.size(2)-1-self.padding),
                          p[..., N:].lt(self.padding)+p[..., N:].gt(x.size(3)-1-self.padding)], dim=-1).type_as(p)
        mask = mask.detach()
        # 相当于求双线性插值中的u和v
        floor_p = p - (p - torch.floor(p))
        p = p*(1-mask) + floor_p*mask
        p = torch.cat([torch.clamp(p[..., :N], 0, x.size(2)-1), torch.clamp(p[..., N:], 0, x.size(3)-1)], dim=-1)

        # bilinear kernel (b, h, w, N)
        # 插值的4个系数
        g_lt = (1 + (q_lt[..., :N].type_as(p) - p[..., :N])) * (1 + (q_lt[..., N:].type_as(p) - p[..., N:]))
        g_rb = (1 - (q_rb[..., :N].type_as(p) - p[..., :N])) * (1 - (q_rb[..., N:].type_as(p) - p[..., N:]))
        g_lb = (1 + (q_lb[..., :N].type_as(p) - p[..., :N])) * (1 - (q_lb[..., N:].type_as(p) - p[..., N:]))
        g_rt = (1 - (q_rt[..., :N].type_as(p) - p[..., :N])) * (1 + (q_rt[..., N:].type_as(p) - p[..., N:]))

        # (b, c, h, w, N)
        x_q_lt = self._get_x_q(x, q_lt, N)
        x_q_rb = self._get_x_q(x, q_rb, N)
        x_q_lb = self._get_x_q(x, q_lb, N)
        x_q_rt = self._get_x_q(x, q_rt, N)

        # (b, c, h, w, N)
        # 插值的最终操作在这里
        x_offset = g_lt.unsqueeze(dim=1) * x_q_lt + \
                   g_rb.unsqueeze(dim=1) * x_q_rb + \
                   g_lb.unsqueeze(dim=1) * x_q_lb + \
                   g_rt.unsqueeze(dim=1) * x_q_rt

        x_offset = self._reshape_x_offset(x_offset, ks)
        out = self.conv_kernel(x_offset)

        return out

    def _get_p_n(self, N, dtype):
        p_n_x, p_n_y = np.meshgrid(range(-(self.kernel_size-1)//2, (self.kernel_size-1)//2+1),
                          range(-(self.kernel_size-1)//2, (self.kernel_size-1)//2+1), indexing='ij')
        # (2N, 1)
        p_n = np.concatenate((p_n_x.flatten(), p_n_y.flatten()))
        p_n = np.reshape(p_n, (1, 2*N, 1, 1))
        p_n = Variable(torch.from_numpy(p_n).type(dtype), requires_grad=False)

        return p_n

    @staticmethod
    def _get_p_0(h, w, N, dtype):
        p_0_x, p_0_y = np.meshgrid(range(1, h+1), range(1, w+1), indexing='ij')
        p_0_x = p_0_x.flatten().reshape(1, 1, h, w).repeat(N, axis=1)
        p_0_y = p_0_y.flatten().reshape(1, 1, h, w).repeat(N, axis=1)
        p_0 = np.concatenate((p_0_x, p_0_y), axis=1)
        p_0 = Variable(torch.from_numpy(p_0).type(dtype), requires_grad=False)

        return p_0

    def _get_p(self, offset, dtype):
        # N = 9, h = 3, w = 3
        N, h, w = offset.size(1)//2, offset.size(2), offset.size(3)

        # (1, 2N, 1, 1)
        p_n = self._get_p_n(N, dtype)
        # (1, 2N, h, w)
        p_0 = self._get_p_0(h, w, N, dtype)
        p = p_0 + p_n + offset
        return p

    def _get_x_q(self, x, q, N):
        b, h, w, _ = q.size()
        padded_w = x.size(3)
        c = x.size(1)
        # (b, c, h*w)
        x = x.contiguous().view(b, c, -1)

        # (b, h, w, N)
        index = q[..., :N]*padded_w + q[..., N:]  # offset_x*w + offset_y
        # (b, c, h*w*N)
        index = index.contiguous().unsqueeze(dim=1).expand(-1, c, -1, -1, -1).contiguous().view(b, c, -1)

        x_offset = x.gather(dim=-1, index=index).contiguous().view(b, c, h, w, N)

        return x_offset

    @staticmethod
    def _reshape_x_offset(x_offset, ks):
        b, c, h, w, N = x_offset.size()
        x_offset = torch.cat([x_offset[..., s:s+ks].contiguous().view(b, c, h, w*ks) for s in range(0, N, ks)], dim=-1)
        x_offset = x_offset.contiguous().view(b, c, h*ks, w*ks)

        return x_offset

这个代码给我们完整的展示了可变形卷积的实现过程，结合上面的DCN实现的详细过程描述以及双线性插值的原理大概可以明白个60%，剩下的40%可以自己去DEBUG跟踪变量进行体会。

6. 总结¶

DCN V1的代码解析我就分析到了这里了，最开始有点懵，然后分析了一下双线性插值的原理并结合源码感觉明白了大概的实现。这个代码的Tensor维度变化我都尽量标注了，但我这里还是建议如果你真要懂这个实现最好去手动DEBUG跟踪一下变量，结合上次的DCN V1的论文解读进行体会。

7. 参考¶

欢迎关注GiantPandaCV, 在这里你将看到独家的深度学习分享，坚持原创，每天分享我们学习到的新鲜知识。( • ̀ω•́ )✧

有对文章相关的问题，或者想要加入交流群，欢迎添加BBuf微信：

二维码

为了方便读者获取资料以及我们公众号的作者发布一些Github工程的更新，我们成立了一个QQ群，二维码如下，感兴趣可以加入。

公众号QQ交流群

本文总阅读量次