在这里插入图片描述

开篇的这张图代表ILSVRC历年的Top-5错误率，我会按照以上经典网络出现的时间顺序对他们进行介绍，同时穿插一些其他的经典CNN网络。

前言¶

昨天讲到了ZFNet和VGG Net，并且我们提到VGGNet是2014年ImageNet分类任务的亚军，而冠军就是今天要介绍的GoogLeNet。GoogLeNet的名字不是GoogleNet，而是GoogLeNet，这是为了致敬LeNet。GoogLeNet和AlexNet/VGGNet这类依靠加深网络结构的深度的思想不完全一样。GoogLeNet在加深度的同时做了结构上的创新，引入了一个叫做Inception的结构来代替之前的卷积加激活的经典组件。GoogLeNet在ImageNet分类比赛上的Top-5错误率降低到了6.7%。

创新点¶

提出Inception模块。
使用辅助Loss。
全连接层用简单的平均池化代替。

网络结构¶

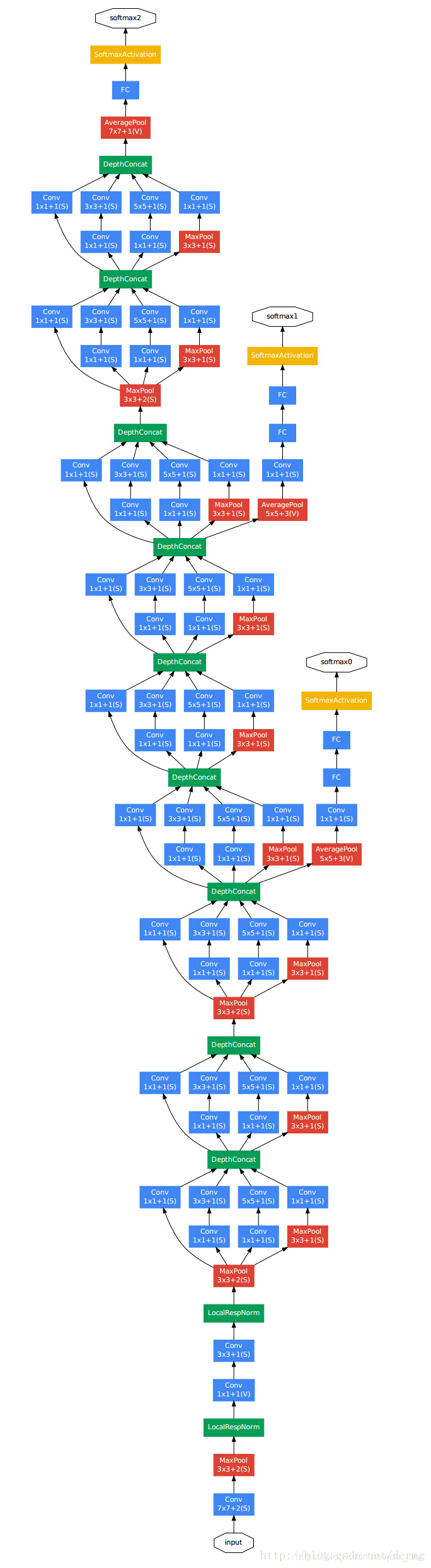
在这里插入图片描述

Inception模块¶

Inception模块在GoogLeNet中设计了两种，一种是原始的Inception模块，一种是带降维的Inception模块，如下图所示：

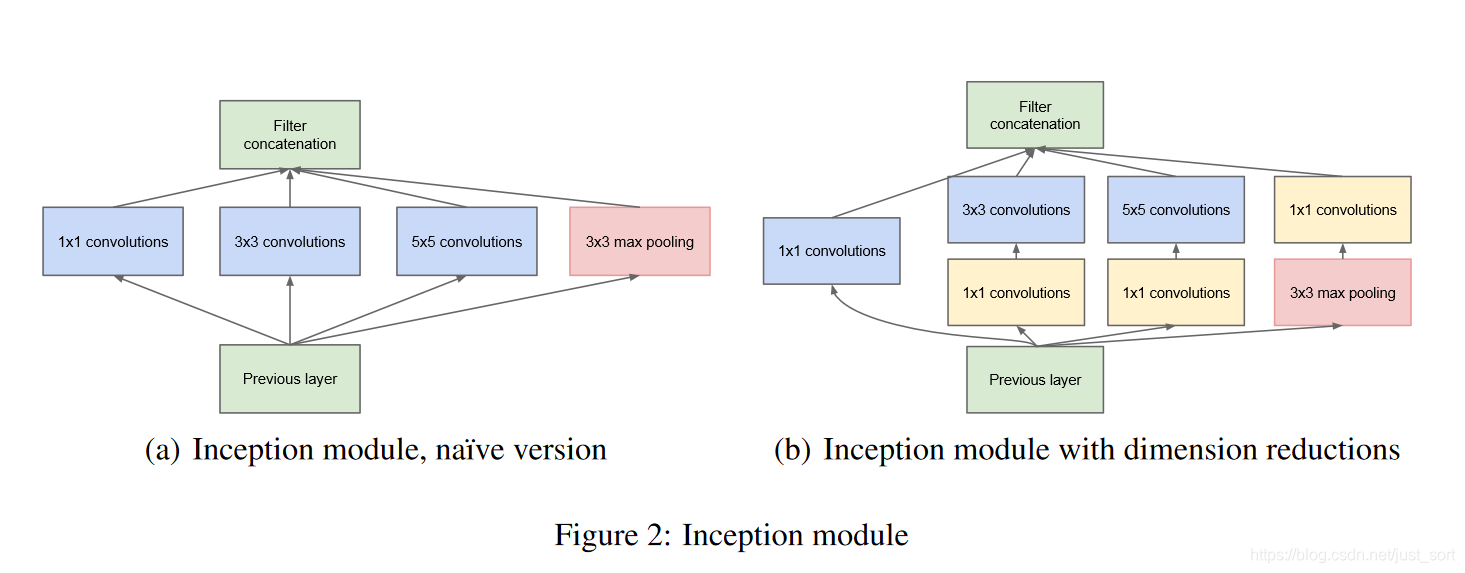
在这里插入图片描述

Inception模块中的卷积步长都是1，另外为了保持特征图大小一致，都设置了Padding方式为Same。每个卷积层后面都接了ReLU激活函数。在输出前有一个Concat层代表把4组不同类型但大小相同的特征响应图堆叠在一起，获得输出特征图。Inception模块一共使用了4种不同大小的卷积核对输入特征图进行了特征提取。并且在原始的Inception模块基础上，为了降低计算量使用 $1\times 1$ 卷积来降维。

关于为什么 $1\times 1$ 卷积可以降维，我们可以举个例子。假设Inception模块的输入特征图通道数为 $256$ ，然后输出特征图的通道数也为 $256$ ，那么对于Inception模块中的 $3\times 3$ 卷积来说，计算量为： $256\times 256\times 3\times 3=589000$ 。而如果使用 $1\times 1$ 卷积降维，那么计算量变成： $(256\times 64\times 1\times 1) + (64 \times 64\times 3\times 3) + (64\times 256\times 1\times 1)=68000$ ，相比于直接使用 $3\times 3$ 卷积降低了大概 $9$ 倍左右的参数量。

辅助损失¶

GoogLeNet有3个损失函数，其中2个是辅助损失。这个设计是为了帮助模型收敛，在中间层加入损失目的是让低层的特征也可以有比较好的区分能力。最后两个辅助损失都被乘以0.3然后加上网络最后的损失作为总的损失来训练GoogLeNet。

将全连接层替换为全局平均池化层¶

GoogleNet将最后的全连接层全部替换为了全局平均池化层，这可以显著减少网络的参数量。AlexNet最后的三个全连接层的参数量占了总参数量的差不多90%，GoogLeNet移除了全连接层使用全局平均池化层进行代替并证明了这种方式实现的精度更好，并且推理速度也明显加快。

GoogLeNet的Keras代码实现¶

def Conv2d_BN(x, nb_filter,kernel_size, padding='same',strides=(1,1),name=None):
    if name is not None:
        bn_name = name + '_bn'
        conv_name = name + '_conv'
    else:
        bn_name = None
        conv_name = None

    x = Conv2D(nb_filter,kernel_size,padding=padding,strides=strides,activation='relu',name=conv_name)(x)
    x = BatchNormalization(axis=3,name=bn_name)(x)
    return x

def Inception(x,nb_filter):
    branch1x1 = Conv2d_BN(x,nb_filter,(1,1), padding='same',strides=(1,1),name=None)

    branch3x3 = Conv2d_BN(x,nb_filter,(1,1), padding='same',strides=(1,1),name=None)
    branch3x3 = Conv2d_BN(branch3x3,nb_filter,(3,3), padding='same',strides=(1,1),name=None)

    branch5x5 = Conv2d_BN(x,nb_filter,(1,1), padding='same',strides=(1,1),name=None)
    branch5x5 = Conv2d_BN(branch5x5,nb_filter,(1,1), padding='same',strides=(1,1),name=None)

    branchpool = MaxPooling2D(pool_size=(3,3),strides=(1,1),padding='same')(x)
    branchpool = Conv2d_BN(branchpool,nb_filter,(1,1),padding='same',strides=(1,1),name=None)

    x = concatenate([branch1x1,branch3x3,branch5x5,branchpool],axis=3)

    return x

def GoogLeNet():
    inpt = Input(shape=(224,224,3))
    #padding = 'same'，填充为(步长-1）/2,还可以用ZeroPadding2D((3,3))
    x = Conv2d_BN(inpt,64,(7,7),strides=(2,2),padding='same')
    x = MaxPooling2D(pool_size=(3,3),strides=(2,2),padding='same')(x)
    x = Conv2d_BN(x,192,(3,3),strides=(1,1),padding='same')
    x = MaxPooling2D(pool_size=(3,3),strides=(2,2),padding='same')(x)
    x = Inception(x,64)#256
    x = Inception(x,120)#480
    x = MaxPooling2D(pool_size=(3,3),strides=(2,2),padding='same')(x)
    x = Inception(x,128)#512
    x = Inception(x,128)
    x = Inception(x,128)
    x = Inception(x,132)#528
    x = Inception(x,208)#832
    x = MaxPooling2D(pool_size=(3,3),strides=(2,2),padding='same')(x)
    x = Inception(x,208)
    x = Inception(x,256)#1024
    x = AveragePooling2D(pool_size=(7,7),strides=(7,7),padding='same')(x)
    x = Dropout(0.4)(x)
    x = Dense(1000,activation='relu')(x)
    x = Dense(1000,activation='softmax')(x)
    model = Model(inpt,x,name='inception')
    return model

结束了吗？¶

GoogLeNet的实际上还有另外一个名字，被叫作Inception V1，之后Google又相继提出了Inception V2/V3/V4。由于Inception V4是在ResNet出现之后提出的，所以这一节就先不讲了，我们来一起看看Inception V2/V3。

Inception V2¶

2015年Google提出了大名鼎鼎的Batch Normalization，即批量归一化并一直被沿用至今。BN的论文地址为：https://arxiv.org/abs/1502.03167 。Inception V2即在InceptionV1的基础上加上了BN层并且将 $5\times 5$ 卷积用两个 $3\times 3$ 卷积代替。

创新点¶

提出了BN层，每次先对输入特征图进行归一化，再送入下一层神经网络输入层。加快了网络的收敛速度。
Conv+BN+Scale+ReLU。Inception V2中每个卷积层后面都有BN层，并且一般BN层还会配合Scale层一起用。
和VGGNet的思想一致，用多个小的卷积核代替大的卷积核，并获得一致的感受野。
进一步加深了网络的深度，使得网络的特征提取能力进一步加强。
增强了模型的非线性表达能力，因为每个卷积后面都加了一个ReLU。卷积层变多，非线性激活函数自然更多，模型的非线性表达能力变得更强。

结构¶

在这里插入图片描述

BatchNorm原理¶

在这里插入图片描述

这是论文中给出的对BatchNorm的算法流程解释，这篇博客的目的主要是推导和实现BatchNorm的前向传播和反向传播，就不关注具体的原理了，我们暂时知道BN层是用来调整数据分布，降低过拟合的就够了。接下来我基于CS231N和Darknet解析一下BatchNorm层的前向和反向传播。

BN的前向传播¶

前向传播实际就是将上面图片的4个公式转化为编程语言，这里我们先贴一段CS231N官方提供的代码：

def batchnorm_forward(x, gamma, beta, bn_param):
  """
  Input:
  - x: (N, D)维输入数据
  - gamma: (D,)维尺度变化参数 
  - beta: (D,)维尺度变化参数
  - bn_param: Dictionary with the following keys:
    - mode: 'train' 或者 'test'
    - eps: 一般取1e-8~1e-4
    - momentum: 计算均值、方差的更新参数
    - running_mean: (D,)动态变化array存储训练集的均值
    - running_var：(D,)动态变化array存储训练集的方差

  Returns a tuple of:
  - out: 输出y_i（N，D）维
  - cache: 存储反向传播所需数据
  """
  mode = bn_param['mode']
  eps = bn_param.get('eps', 1e-5)
  momentum = bn_param.get('momentum', 0.9)

  N, D = x.shape
  # 动态变量，存储训练集的均值方差
  running_mean = bn_param.get('running_mean', np.zeros(D, dtype=x.dtype))
  running_var = bn_param.get('running_var', np.zeros(D, dtype=x.dtype))

  out, cache = None, None
  # TRAIN 对每个batch操作
  if mode == 'train':
    sample_mean = np.mean(x, axis = 0)
    sample_var = np.var(x, axis = 0)
    x_hat = (x - sample_mean) / np.sqrt(sample_var + eps)
    out = gamma * x_hat + beta
    cache = (x, gamma, beta, x_hat, sample_mean, sample_var, eps)
    running_mean = momentum * running_mean + (1 - momentum) * sample_mean
    running_var = momentum * running_var + (1 - momentum) * sample_var
  # TEST：要用整个训练集的均值、方差
  elif mode == 'test':
    x_hat = (x - running_mean) / np.sqrt(running_var + eps)
    out = gamma * x_hat + beta
  else:
    raise ValueError('Invalid forward batchnorm mode "%s"' % mode)

  bn_param['running_mean'] = running_mean
  bn_param['running_var'] = running_var

  return out, cache

这里倒是没啥好说的，不过了为了和下面反向传播对比理解，这里我们明确每一个张量的维度：

x shape为(N,D)，可以将N看成batch size,D看成特征图展开为1列的元素个数
gamma shape为(D,)
beta shape为(D,)
running_mean shape为(D,)
running_var shape为(D,)

BN的反向传播¶

这才是我们的重点，我写过softmax和线性回归的求导，也前后弄清楚了卷积的im2col和卷积的求导，但是BN层的求导一直没弄清楚，现在我们一定要弄清楚，现在做一些约定：

$\delta$ 为一个Batch所有样本的方差
$\mu$ 为样本均值
$\widehat {x}$ 为归一化后的样本数据
$y_i$ 为输入样本 $x_i$ 经过尺度变化的输出量
$\gamma$ 和 $\beta$ 为尺度变化系数
$\dfrac {\partial L} {\partial y}$ 是上一层的梯度，并假设 $x$ 和 $y$ 都是(N,D)维，即有N个维度为D的样本在BN层的前向传播中 $x_i$ 通过 $\gamma$ , $\beta$ , $\widehat{x}$ 将 $x_i$ 变换为 $y_i$ ，那么反向传播则是根据 $\dfrac {\partial L} {\partial y_i}$ 求得 $\dfrac {\partial L} {\partial \gamma}$ , $\dfrac {\partial L} {\partial \beta}$ , $\dfrac {\partial L} {\partial x_i}$ .
求解 $\dfrac {\partial L} {\partial \gamma}$ $\dfrac {\partial L} {\partial \gamma} = \sum_{i}\dfrac {\partial L} {\partial y_i}\dfrac{\partial y_i}{\partial \gamma}=\sum_i\dfrac {\partial L} {\partial y_i}\widehat {x}$
求解 $\dfrac {\partial L} {\partial \beta}$ $\dfrac {\partial L} {\partial \beta}=\sum_i\dfrac {\partial L} {\partial y_i}\dfrac{\partial y_i}{\partial \beta}=\sum_i\dfrac {\partial L} {\partial y_i}$
求解 $\dfrac {\partial L} {\partial x_i}$ 根据论文的公式和链式法则可得下面的等式:

$\dfrac {\partial L} {\partial x_{i}}=\dfrac {\partial L} {\partial \widehat {x_{i}}}\dfrac {\partial \widehat {x_i}}{\partial x_{i}}+\dfrac {\partial L} {\partial \sigma}\dfrac {\partial \sigma}{\partial x_{i}}+\dfrac {\partial L} {\partial \mu}\dfrac {\partial \mu}{\partial x_{i}}$

我们这里又可以先求 $\dfrac {\partial L} {\partial \widehat {x}}$

$\dfrac {\partial L} {\partial \widehat {x}}=\dfrac {\partial L} {\partial y}\dfrac {\partial y} {\partial \widehat {x}} \\ =\dfrac {\partial L} {\partial {y}}\gamma$ (1)
$\dfrac {\partial L} {\partial \sigma}=\sum _{i}\dfrac {\partial L} {\partial y_{i}}\dfrac {\partial y_{i}} {\partial \widehat {x}_{i}}\dfrac {\partial \widehat {x}_{i}}{\partial \sigma} \\ =-\dfrac{1}{2}\sum _{i}\dfrac {\partial L} {\partial \widehat {x_{i}}}(x_{i}-\mu)(\sigma+\varepsilon)^{-1.5}$ (2)
$\dfrac {\partial L} {\partial \mu}=\dfrac {\partial L} {\partial \widehat {x}}\dfrac {\partial \widehat {x}}{\partial \mu}+\dfrac {\partial L} {\partial \sigma}\dfrac {\partial \sigma}{\partial \mu} \\ =\sum _{i}\dfrac {\partial L} {\partial \widehat {x}_{i}}\dfrac {-1}{\sqrt {\sigma+ \varepsilon}}+\dfrac {\partial L} {\partial \sigma}\dfrac {-2\Sigma _{i}\left( x_{i}-\mu\right) } {N}$ (3)

有了(1),(2),(3)就可以求出 $\dfrac {\partial L} {\partial x_{i}}$

$\dfrac {\partial L} {\partial x_{i}}=\dfrac {\partial L} {\partial \widehat {x_{i}}}\dfrac {\partial \widehat {x_i}}{\partial x_{i}}+\dfrac {\partial L} {\partial \sigma}\dfrac {\partial \sigma}{\partial x_{i}}+\dfrac {\partial L} {\partial \mu}\dfrac {\partial \mu}{\partial x_{i}} \\ =\dfrac {\partial L} {\partial \widehat {x}_{i}}\dfrac {1}{\sqrt {\sigma+ \varepsilon}}+\dfrac {\partial L} {\partial \sigma}\dfrac{2(x_i-\mu)}{N}+\dfrac {\partial L} {\partial \mu}\dfrac {1}{N}$

到这里就推到出了BN层的反向传播公式了，和论文中一样，截取一下论文中的结果图：

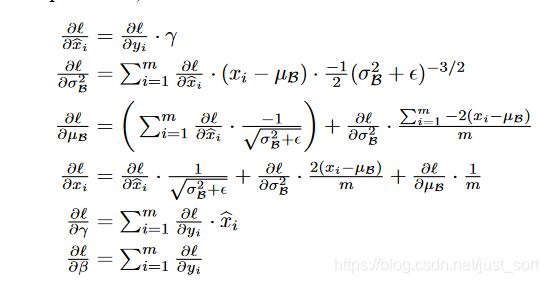
在这里插入图片描述

贴一份CS231N代码：

def batchnorm_backward(dout, cache):
  """
  Inputs:
  - dout: 上一层的梯度，维度(N, D)，即 dL/dy
  - cache: 所需的中间变量，来自于前向传播

  Returns a tuple of:
  - dx: (N, D)维的 dL/dx
  - dgamma: (D,)维的dL/dgamma
  - dbeta: (D,)维的dL/dbeta
  """
    x, gamma, beta, x_hat, sample_mean, sample_var, eps = cache
  N = x.shape[0]

  dgamma = np.sum(dout * x_hat, axis = 0)
  dbeta = np.sum(dout, axis = 0)

  dx_hat = dout * gamma
  dsigma = -0.5 * np.sum(dx_hat * (x - sample_mean), axis=0) * np.power(sample_var + eps, -1.5)
  dmu = -np.sum(dx_hat / np.sqrt(sample_var + eps), axis=0) - 2 * dsigma*np.sum(x-sample_mean, axis=0)/ N
  dx = dx_hat /np.sqrt(sample_var + eps) + 2.0 * dsigma * (x - sample_mean) / N + dmu / N

  return dx, dgamma, dbeta

DarkNet中的BN层¶

darknet中在src/blas.h中实现了前向传播的几个公式：

/*
** 计算输入数据x的平均值，输出的mean是一个矢量，比如如果x是多张三通道的图片，那么mean的维度就为通道3
** 由于每次训练输入的都是一个batch的图片，因此最终会输出batch张三通道的图片，mean中的第一个元素就是第
** 一个通道上全部batch张输出特征图所有元素的平均值，本函数的用处之一就是batch normalization的第一步了
** x: 包含所有数据，比如l.output，其包含的元素个数为l.batch*l.outputs
** batch: 一个batch中包含的图片张数，即l.batch
** filters: 该层神经网络的滤波器个数，也即该层网络输出图片的通道数（比如对卷积网络来说，就是核的个数了）
** spatial: 该层神经网络每张输出特征图的尺寸，也即等于l.out_w*l.out_h
** mean: 求得的平均值，维度为filters，也即每个滤波器对应有一个均值（每个滤波器会处理所有图片）
** x的内存排布？此处还是结合batchnorm_layer.c中的forward_batch_norm_layer()函数的调用来解释，其中x为l.output，其包含的元素个数为l
** 有l.batch行，每行有l.out_c*l.out_w*l.out_h个元素，每一行又可以分成l.out_c行，l.out_w*l.out_h列，
** 那么l.mean中的每一个元素，是某一个通道上所有batch的输出的平均值
** （比如卷积层，有3个核，那么输出通道有3个，每张输入图片都会输出3张特征图，可以理解每张输出图片是3通道的，
** 若每次输入batch=64张图片，那么将会输出64张3通道的图片，而mean中的每个元素就是某个通道上所有64张图片
** 所有元素的平均值，比如第1个通道上，所有64张图片像素平均值）
*/
void mean_cpu(float *x, int batch, int filters, int spatial, float *mean)
{
    // scale即是均值中的分母项
    float scale = 1./(batch * spatial);
    int i,j,k;
    // 外循环次数为filters，也即mean的维度，每次循环将得到一个平均值
    for(i = 0; i < filters; ++i){
        mean[i] = 0;
        // 中间循环次数为batch，也即叠加每张输入图片对应的某一通道上的输出
        for(j = 0; j < batch; ++j){
            // 内层循环即叠加一张输出特征图的所有像素值
            for(k = 0; k < spatial; ++k){
                // 计算偏移
                int index = j*filters*spatial + i*spatial + k;
                mean[i] += x[index];
            }
        }
        mean[i] *= scale;
    }
}

/*
** 计算输入x中每个元素的方差
** 本函数的主要用处应该就是batch normalization的第二步了
** x: 包含所有数据，比如l.output，其包含的元素个数为l.batch*l.outputs
** batch: 一个batch中包含的图片张数，即l.batch
** filters: 该层神经网络的滤波器个数，也即是该网络层输出图片的通道数
** spatial: 该层神经网络每张特征图的尺寸，也即等于l.out_w*l.out_h
** mean: 求得的平均值，维度为filters，也即每个滤波器对应有一个均值（每个滤波器会处理所有图片）
*/
void variance_cpu(float *x, float *mean, int batch, int filters, int spatial, float *variance)
{
    // 这里计算方差分母要减去1的原因是无偏估计，可以看：https://www.zhihu.com/question/20983193
    // 事实上，在统计学中，往往采用的方差计算公式都会让分母减1,这时因为所有数据的方差是基于均值这个固定点来计算的，
    // 对于有n个数据的样本，在均值固定的情况下，其采样自由度为n-1（只要n-1个数据固定，第n个可以由均值推出）
    float scale = 1./(batch * spatial - 1);
    int i,j,k;
    for(i = 0; i < filters; ++i){
        variance[i] = 0;
        for(j = 0; j < batch; ++j){
            for(k = 0; k < spatial; ++k){
                int index = j*filters*spatial + i*spatial + k;
                // 每个元素减去均值求平方
                variance[i] += pow((x[index] - mean[i]), 2);
            }
        }
        variance[i] *= scale;
    }
}
void normalize_cpu(float *x, float *mean, float *variance, int batch, int filters, int spatial)
{
    int b, f, i;
    for(b = 0; b < batch; ++b){
        for(f = 0; f < filters; ++f){
            for(i = 0; i < spatial; ++i){
                int index = b*filters*spatial + f*spatial + i;
                x[index] = (x[index] - mean[f])/(sqrt(variance[f]) + .000001f);
            }
        }
    }
}
/*
** axpy 是线性代数中的一种基本操作(仿射变换)完成y= alpha*x + y操作，其中x,y为矢量，alpha为实数系数，
** 请看: https://www.jianshu.com/p/e3f386771c51
** N: X中包含的有效元素个数
** ALPHA: 系数alpha
** X: 参与运算的矢量X
** INCX: 步长(倍数步长)，即x中凡是INCX倍数编号的参与运算
** Y: 参与运算的矢量，也相当于是输出
*/
void axpy_cpu(int N, float ALPHA, float *X, int INCX, float *Y, int INCY)
{
    int i;
    for(i = 0; i < N; ++i) Y[i*INCY] += ALPHA*X[i*INCX];
}

void scal_cpu(int N, float ALPHA, float *X, int INCX)
{
    int i;
    for(i = 0; i < N; ++i) X[i*INCX] *= ALPHA;
}

在src/batchnorm_layer.c中实现了前向传播和反向传播的接口函数：

// BN层的前向传播函数
void forward_batchnorm_layer(layer l, network net)
{
    if(l.type == BATCHNORM) copy_cpu(l.outputs*l.batch, net.input, 1, l.output, 1);
    copy_cpu(l.outputs*l.batch, l.output, 1, l.x, 1);
    // 训练阶段
    if(net.train){
        // blas.c中有详细注释，计算输入数据的均值，保存为l.mean
        mean_cpu(l.output, l.batch, l.out_c, l.out_h*l.out_w, l.mean);
        // blas.c中有详细注释，计算输入数据的方差，保存为l.variance
        variance_cpu(l.output, l.mean, l.batch, l.out_c, l.out_h*l.out_w, l.variance);

        // 计算滑动平均和方差，影子变量，可以参考https://blog.csdn.net/just_sort/article/details/100039418
        scal_cpu(l.out_c, .99, l.rolling_mean, 1);
        axpy_cpu(l.out_c, .01, l.mean, 1, l.rolling_mean, 1);
        scal_cpu(l.out_c, .99, l.rolling_variance, 1);
        axpy_cpu(l.out_c, .01, l.variance, 1, l.rolling_variance, 1);
        // 减去均值，除以方差得到x^，论文中的第3个公式
        normalize_cpu(l.output, l.mean, l.variance, l.batch, l.out_c, l.out_h*l.out_w);  
        // BN层的输出
        copy_cpu(l.outputs*l.batch, l.output, 1, l.x_norm, 1);
    } else {
        // 测试阶段，直接用滑动变量来计算输出
        normalize_cpu(l.output, l.rolling_mean, l.rolling_variance, l.batch, l.out_c, l.out_h*l.out_w);
    }
    // 最后一个公式，对输出进行移位和偏置
    scale_bias(l.output, l.scales, l.batch, l.out_c, l.out_h*l.out_w);
    add_bias(l.output, l.biases, l.batch, l.out_c, l.out_h*l.out_w);
}

// BN层的反向传播函数
void backward_batchnorm_layer(layer l, network net)
{
    // 如果在测试阶段，均值和方差都可以直接用滑动变量来赋值
    if(!net.train){
        l.mean = l.rolling_mean;
        l.variance = l.rolling_variance;
    }
    // 在卷积层中定义了backward_bias，并有详细注释
    backward_bias(l.bias_updates, l.delta, l.batch, l.out_c, l.out_w*l.out_h);
    // 这里是对论文中最后一个公式的缩放系数求梯度更新值
    backward_scale_cpu(l.x_norm, l.delta, l.batch, l.out_c, l.out_w*l.out_h, l.scale_updates);
    // 也是在convlution_layer.c中定义的函数，先将敏感度图乘以l.scales
    scale_bias(l.delta, l.scales, l.batch, l.out_c, l.out_h*l.out_w);

    // 对应了https://blog.csdn.net/just_sort/article/details/100039418 中对均值求导数
    mean_delta_cpu(l.delta, l.variance, l.batch, l.out_c, l.out_w*l.out_h, l.mean_delta);
    // 对应了https://blog.csdn.net/just_sort/article/details/100039418 中对方差求导数
    variance_delta_cpu(l.x, l.delta, l.mean, l.variance, l.batch, l.out_c, l.out_w*l.out_h, l.variance_delta);
    // 计算敏感度图，对应了论文中的最后一部分
    normalize_delta_cpu(l.x, l.mean, l.variance, l.mean_delta, l.variance_delta, l.batch, l.out_c, l.out_w*l.out_h, l.delta);
    if(l.type == BATCHNORM) copy_cpu(l.outputs*l.batch, l.delta, 1, net.delta, 1);
}

其中反向传播的函数如下，就是利用我们推导出的公式来计算：

// 这里是对论文中最后一个公式的缩放系数求梯度更新值
// x_norm 代表BN层前向传播的输出值
// delta 代表上一层的梯度图
// batch 为l.batch，即一个batch的图片数
// n代表输出通道数，也即是输入通道数
// size 代表w * h
// scale_updates 代表scale的梯度更新值
// y = gamma * x + beta
// dy / d(gamma) = x
void backward_scale_cpu(float *x_norm, float *delta, int batch, int n, int size, float *scale_updates)
{
    int i,b,f;
    for(f = 0; f < n; ++f){
        float sum = 0;
        for(b = 0; b < batch; ++b){
            for(i = 0; i < size; ++i){
                int index = i + size*(f + n*b);
                sum += delta[index] * x_norm[index];
            }
        }
        scale_updates[f] += sum;
    }
}

// 对均值求导
// 对应了论文中的求导公式3，不过Darknet特殊的点在于是先计算均值的梯度
// 这个时候方差是没有梯度的，所以公式3的后半部分为0，也就只保留了公式3的前半部分
// 不过我从理论上无法解释这种操作会带来什么影响，但从目标检测来看应该是没有影响的
void mean_delta_cpu(float *delta, float *variance, int batch, int filters, int spatial, float *mean_delta)
{

    int i,j,k;
    for(i = 0; i < filters; ++i){
        mean_delta[i] = 0;
        for (j = 0; j < batch; ++j) {
            for (k = 0; k < spatial; ++k) {
                int index = j*filters*spatial + i*spatial + k;
                mean_delta[i] += delta[index];
            }
        }
        mean_delta[i] *= (-1./sqrt(variance[i] + .00001f));
    }
}
// 对方差求导
// 对应了论文中的求导公式2
void  variance_delta_cpu(float *x, float *delta, float *mean, float *variance, int batch, int filters, int spatial, float *variance_delta)
{
    int i,j,k;
    for(i = 0; i < filters; ++i){
        variance_delta[i] = 0;
        for(j = 0; j < batch; ++j){
            for(k = 0; k < spatial; ++k){
                int index = j*filters*spatial + i*spatial + k;
                variance_delta[i] += delta[index]*(x[index] - mean[i]);
            } 
        }
        variance_delta[i] *= -.5 * pow(variance[i] + .00001f, (float)(-3./2.));
    }
}
// 求出BN层的梯度敏感度图
// 对应了论文中的求导公式4，即是对x_i求导
void normalize_delta_cpu(float *x, float *mean, float *variance, float *mean_delta, float *variance_delta, int batch, int filters, int spatial, float *delta)
{
    int f, j, k;
    for(j = 0; j < batch; ++j){
        for(f = 0; f < filters; ++f){
            for(k = 0; k < spatial; ++k){
                int index = j*filters*spatial + f*spatial + k;
                delta[index] = delta[index] * 1./(sqrt(variance[f] + .00001f)) + variance_delta[f] * 2. * (x[index] - mean[f]) / (spatial * batch) + mean_delta[f]/(spatial*batch);
            }
        }
    }
}

Inception V3¶

在InceptionV2的基础上做了微小的改变就获得了Inception V3，Inception V3模块的结构为：

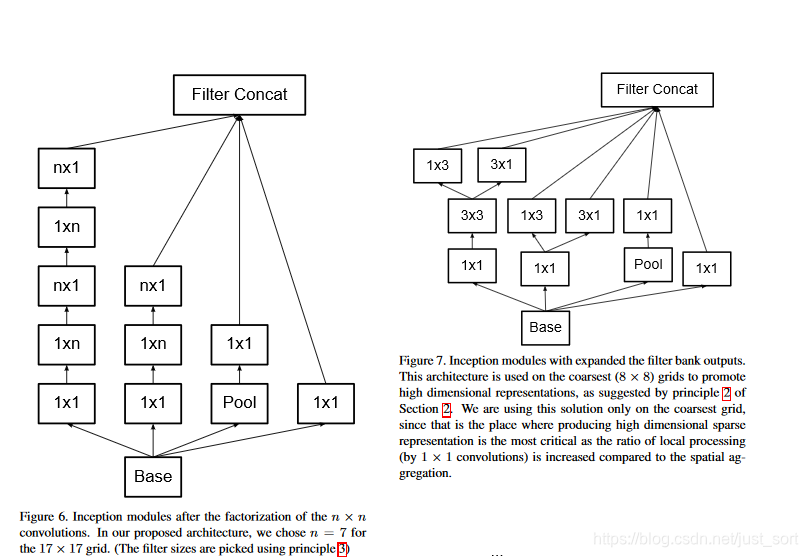
在这里插入图片描述

而InceptionV3的网络结构为：

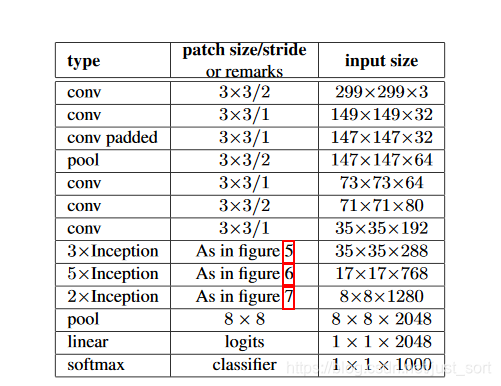
在这里插入图片描述

Inception系列网络的一些Trick¶

辅助分类器。介绍Inception V1(Google Net)的时候我已经介绍过了，这种损失现在已经被称为多任务损失了，典型的如目标检测中的分类和回归损失。
标签平滑。在比赛中经常用到，以前构造标签的时候实际是哪一类就置1，其他类的都置为0，不够平滑，学习时就会很难，容易过拟合。所以标签平滑就是给真实标签最大值，也按照概率给其他类一些值，如给一些根号值。
使用合适的方法下采样，具体如下图所示。

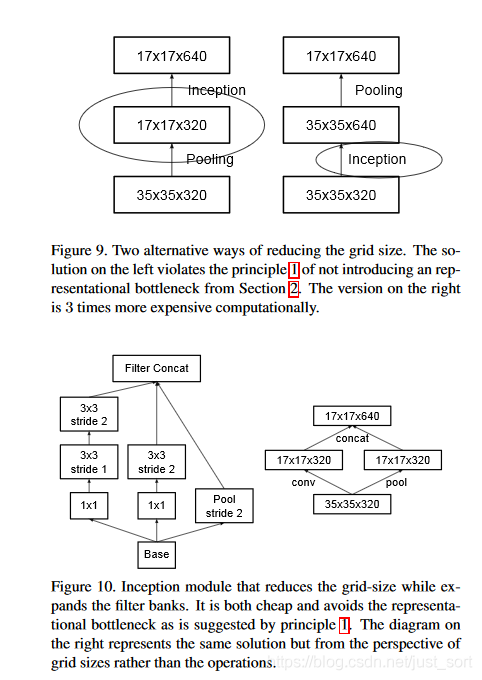
在这里插入图片描述

其中Figure9（a）表示先直接下采样再增加通道数，直接下采样很容易丢掉一些表征信息，这些信息学不到模型可能就会有瓶颈。而Figure9（b）表示先增加通道数再直接下采样，先增加通道数时参数会增大了很多倍，太复杂，耗内存，计算量大。Figure10（a）用了两层的 $3\times 3$ 卷积，步长变大，图像也可以缩小，即代替Pooling来下采样。Figure10（d）是最好的方案，即把特征图拆成2部分，一部分直接采样（pooling），一个做卷积（下采样），再把两种信息连到一起，这样通过分开的方式相对于以前的方法挖掘到不同的信息更多，因为卷积和pooling都是在原始特征图上做的。

实验结果¶

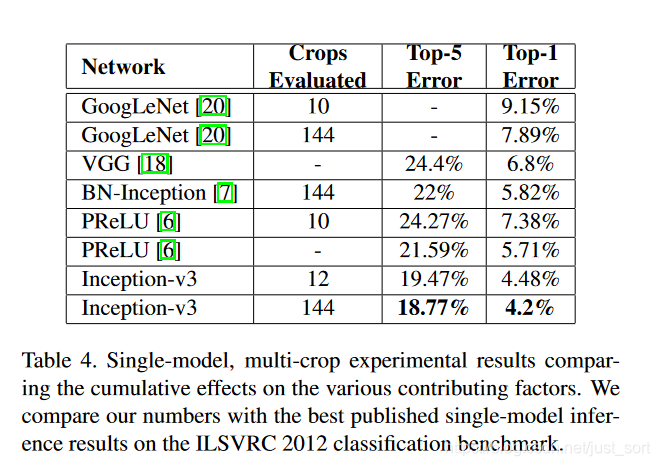
在这里插入图片描述

总结¶

GoogLeNet系列有相当多有价值的东西，可以说GoogLeNet是卷积神经网络历史长河中的大浪推手，Inception模块设计的思维和结构即是是今天依然被广泛应用。

附录¶

参考资料1：https://blog.csdn.net/yuechuen/article/details/71502503

参考资料2：https://github.com/lightaime/cs231n/blob/master/assignment2/cs231n/layers.py

参考资料3：https://blog.csdn.net/xiaojiajia007/article/details/54924959

BN的原文：https://arxiv.org/abs/1502.03167

InceptionV2/V3论文原文：https://arxiv.org/abs/1512.00567

卷积神经网络学习路线往期文章¶

欢迎关注我的微信公众号GiantPandaCV，期待和你一起交流机器学习，深度学习，图像算法，优化技术，比赛及日常生活等。

图片.png

本文总阅读量次