前言¶

上一篇推文介绍了卷积神经网络的组成层以及卷积层是如何在图像中起作用的，推文地址为：https://mp.weixin.qq.com/s/MxYjW02rWfRKPMwez02wFA 。今天我们就继续讲讲卷积核的基本参数以及卷积核有哪些基本类型。

卷积核的基本参数¶

卷积神经网络的核心操作就是卷积层，我们这里以caffe框架为例子来介绍一下卷积核都有哪些基本的参数。下面先上一段代码，是caffe的卷积层的配置文件：

layer {
  name: "conv1"
  type: "Convolution"
  bottom: "data"
  top: "conv1"
  param {
    lr_mult: 1
  }
  param {
    lr_mult: 2
  }
  convolution_param {
    num_output: 20
    kernel_size: 5
    stride: 1
    weight_filler {
      type: "xavier"
    }
    bias_filler {
      type: "constant"
    }
  }
}

从上面我们可以看到卷积层的参数有：

• lr_mult：学习率的系数，最终的学习率是这个参数乘以caffe的solver.prototxt配置文件中的基础学习率base_lr。如果有2个lr_mult，则第一个表示权值的学习率，第二个表示偏置项的学习率。一般偏置项的学习率是权值项的学习率的2倍。
• num_output：卷积核的输出通道数。若设置为与输入通道数一样的大小，可以保持输入输出维度的一致性；若采用比输入通道数更小的值，则可以减少整体网络的参数量
• kernel_size：卷积核的大小。如果卷积核的长和宽不等，需要用kernel_h和kernel_w分别设定其它参数。
• stride：卷积核的步长，默认为1。当然也可以用stride_h和stride_w来设置。
• pad：扩充边缘，默认为0，不扩充。 扩充的时候是左右、上下对称的，比如卷积核的大小为$5\times 5$，那么pad设置为2，则四个边缘都扩充2个像素，即宽度和高度都扩充了4个像素,这样卷积运算之后的特征图就不会变小。也可以通过pad_h和pad_w来分别设定。
• weight_filler：权重初始化方式。有xavier,gaussian，及constant等方式。
• bias_filler: 偏置项的初始化。一般设置为constant,值全为0。
• bias_term：是否开启偏置项，默认为true，开启。
• group： 分组，默认为1组。如果大于1，我们限制卷积的连接操作在一个子集内。如果我们根据图像的通道来分组，那么第i个输出分组只能与第i个输入分组进行连接。
• num_input： 输入通道数，这个包含在bottom中，所以实际上没有这个参数哦，只是可以这样理解。

现在设输入通道数为c0，输出通道数为c1，那么输入可以表示为$[n, c0, w0, h0]$，输出可以表示为：$[n, c1, w1, h1]$。其中$w0,h0$表示输入特征图的长宽，那么输出特征图的长宽$w1,h1$可以用下面的公式计算：

$w1=(w0+2\times pad-kernel_w)/stride+1$

$h1=(h0+2\times pad-kernel_h)/stride+1$

如果将stride设为1，前后两次卷积部分存在重叠，如果设置pad=(kernel_size-1)/2，那么输出特征图的高宽都不变。

常用卷积核类型盘点？¶

卷积核的类型有很多，从我在工业上做的一些任务来看，最常用的卷积核类型大概有4种，分别是标准卷积，扩张卷积，转置卷积和深度可分离卷积。所以本节我就 介绍一下这4种卷积希望可以抛砖引玉，引起大家对卷积核探索的兴趣。这里要先说一个感受野的概念，所谓感受野就是是卷积神经网络每一层输出的特征图（feature map）上的像素点在输入图片上映射的区域大小。再通俗点的解释是，特征图上的一个点对应输入图上的区域。

标准卷积¶

这是我们最常用的卷积，连续紧密的矩阵形式可以提取图像区域中相邻像素之间的关联性，例如一个$3\times 3$的卷积核可以获得$3\times 3$的感受野。如下图所示：

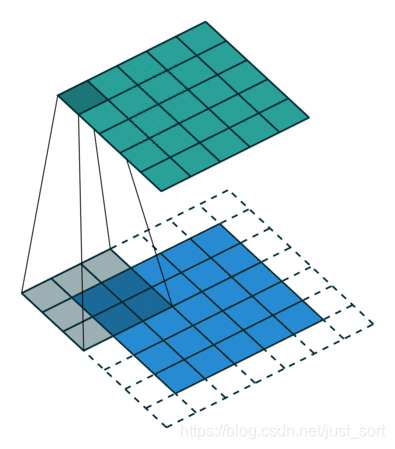
转置卷积¶

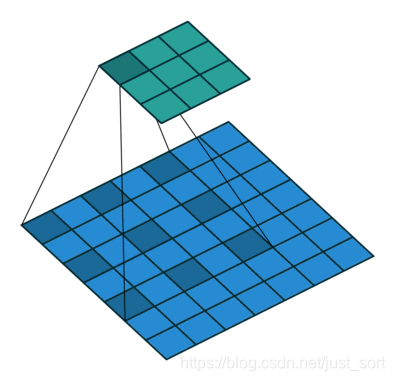
转置卷积是先对原始特征矩阵进行填充使其维度扩大到目标输出维度，然后进行普通的卷积操作的过程，其输入到输出的维度变换关系恰好和普通的卷积变换关系相反，但这个变换并不是卷积真正的逆变换操作，我们通常将其称为转置卷积(Transpose Convolution)而不是反卷积(Deconvolution)。转置卷积常见于目标检测领域中对小目标的检测以及图像分割领域还原输入图像尺度如FCN中。如下图所示，其中下图数输入，上图是输出：

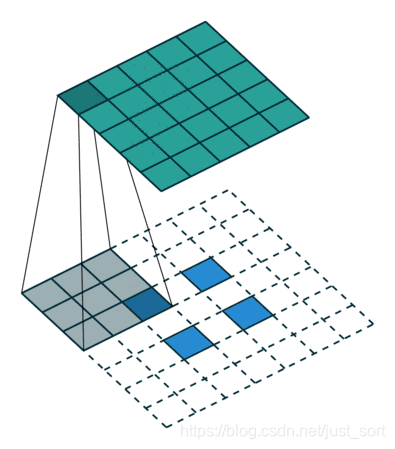
扩张卷积（带孔卷积或空洞卷积）¶

这是一种特殊的卷积，引入了一个称为扩展率(Dilation Rate)的参数，使得同样尺寸的卷积核可以获得更大的感受野，相应的在相同感受视野的前提下比普通卷积采用更少的参数。举个例子，同样是$3\times 3$卷积核，扩张卷积可以获得$5\times 5$范围的区域特征，在图像分割领域被广泛应用。如下图所示：

深度可分离卷积¶

这是在轻量级模型算法优化中经常会使用到的一种卷积方式，标准的卷积操作是对原始图像$H\times W\times C$三个方向的卷积运算，假设现在有$K$个相同尺寸卷积核，这样的操作计算量为$H\times W\times C\times K$个。若将长宽与深度方向的卷积操作分离出变为$H\times W$与$C$的两个卷积操作，则同样的卷积核数量$K$，现在的计算量变成了$(H\times W + C)\times K$个，也可以得到相同维度的输出。深度可分离卷积在模型压缩和一些轻量级卷积神经网络中被广泛应用。

后记¶

今天这篇推文没有什么骚操作，就是回归了一下卷积核的参数以及卷积核的4种基础类型，因为这4种是一直在用的，所以就在这里说了。其他的卷积类型可能之后我的经典网络论文解读系列中会提到，今天就说到这里啦。

欢迎关注我的微信公众号GiantPandaCV，期待和你一起交流机器学习，深度学习，图像算法，优化技术，比赛及日常生活等。