在这里插入图片描述

开篇的这张图代表ILSVRC历年的Top-5错误率，我会按照以上经典网络出现的时间顺序对他们进行介绍，同时穿插一些其他的经典CNN网络。

前言¶

时间来到2016年，也就是ResNet被提出的下一年，清华的黄高(也是DenseNet的提出者)在EECV会议上提出了Stochastic Depth（随机深度网络）。这个网络主要是针对ResNet训练时做了一些优化，即随机丢掉一些层，优化了速度和性能(有点类似于Dropout的效果？)。论文原文见附录。

背景¶

ResNet这个里程碑式的创新对AI领域带来了深远的影响。然而，作者发现ResNet网络中不是所有的层都是必要的，因此结合经典的Dropout思想提出在训练过程中随机丢弃丢掉一些层来优化ResNet的训练过程。(PS：这不就是把Dropout用到网络层这个单位吗？)

结构¶

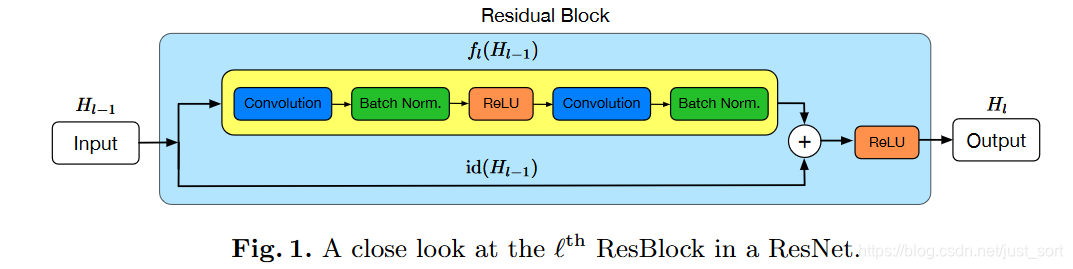
首先来看一下原始的ResNet结构，其中 $f$ 代表的是残差部分， $id$ 代表的是恒等映射，把这两部分求和经过激活然后然后输出。这个过程可以用下面的式子来表示：

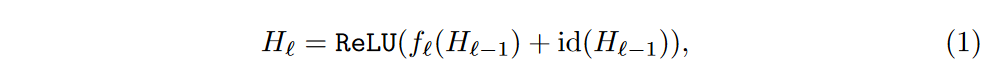
在这里插入图片描述

如下图所示：

在这里插入图片描述

Stochastic Depth(随机深度网络)就是在训练时加入了一个随机变量 $b$ ，其中 $b$ 的概率分布是满足一个伯努利分布的，然后将 $f$ 乘以 $b$ ，对残差部分做了随机丢弃。如果 $b=1$ ，这个结构即是原始的ResNet结构，而当 $b=0$ 时，残差支路没有被激活，整个结构退化为一个恒等函数。这个过程可以用下面的等式来表示：

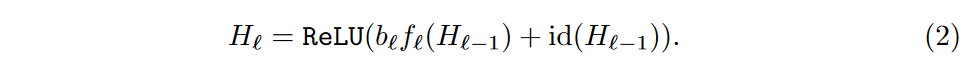
在这里插入图片描述

上面提到 $b$ 满足一个伯努利分布(01分布)，它的取值只有 $0$ 和 $1$ 两种，其中取 $0$ 的概率为 $1-p$ ，取 $1$ 的概率是 $p$ 。上面的 $p$ 又被称为生存概率，这个 $p$ 即代表了 $b=1$ 的可能性，因此 $p$ 的设置相当重要。

一种设置方式是将其设置为同一个值，即 $p_l=p$ ，其中 $p_l$ 代表每个残差块 $l$ 的 $p$ 参数取值。
另外一种设置方式是将其设置为残差层数 $l$ 的平滑函数。从 $p_0=1$ 线性递减到 $p_L=0.5$ ，一共有L个残差块。公式表示如下：

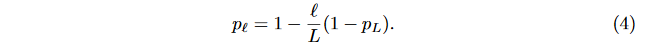
在这里插入图片描述

论文选择了第二种设置方式，即将线性衰减规律应用于每一层的生存概率的设置，这是因为较早的层会提取低级特征，而这些低级特征会被后面的特征应用，因此前面的层不应该频繁的被丢弃，最终 $p$ 产生的规则如Figure2所示。

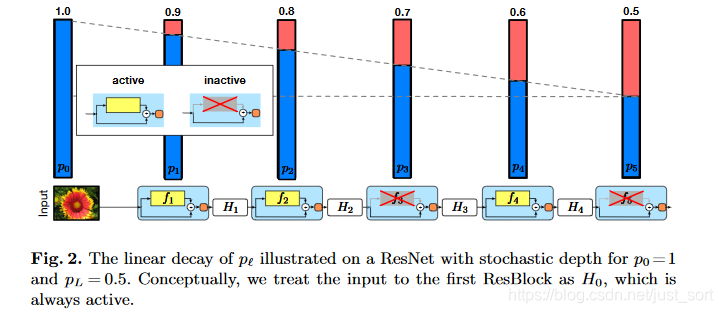
在这里插入图片描述

论文中提到，将原始的ResNet模型调整为随机深度网络之后，期望深度为原始ResNet的 $\frac{3}{4}$ ，并且训练过程提速 $40$ %，这个可以自己做实验验证。等等， $\frac{3}{4}$ 怎么来的？看看下图就懂了。

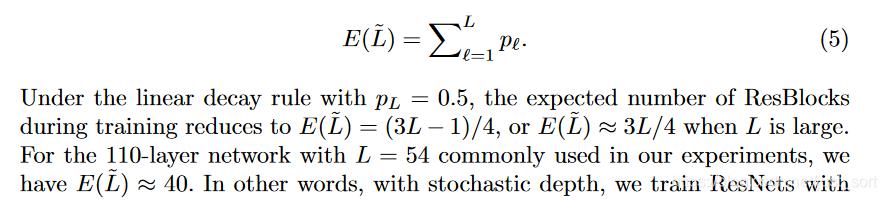
在这里插入图片描述

测试¶

在测试过程中，所有的残差块都保持被激活的状态，以充分利用整个网络的所有参数。但每个残差块的权重都要根据其在训练中的生存概率 $p$ 进行重新调整，具体来说，前向传播的公式如下：

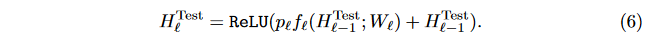
在这里插入图片描述

实验¶

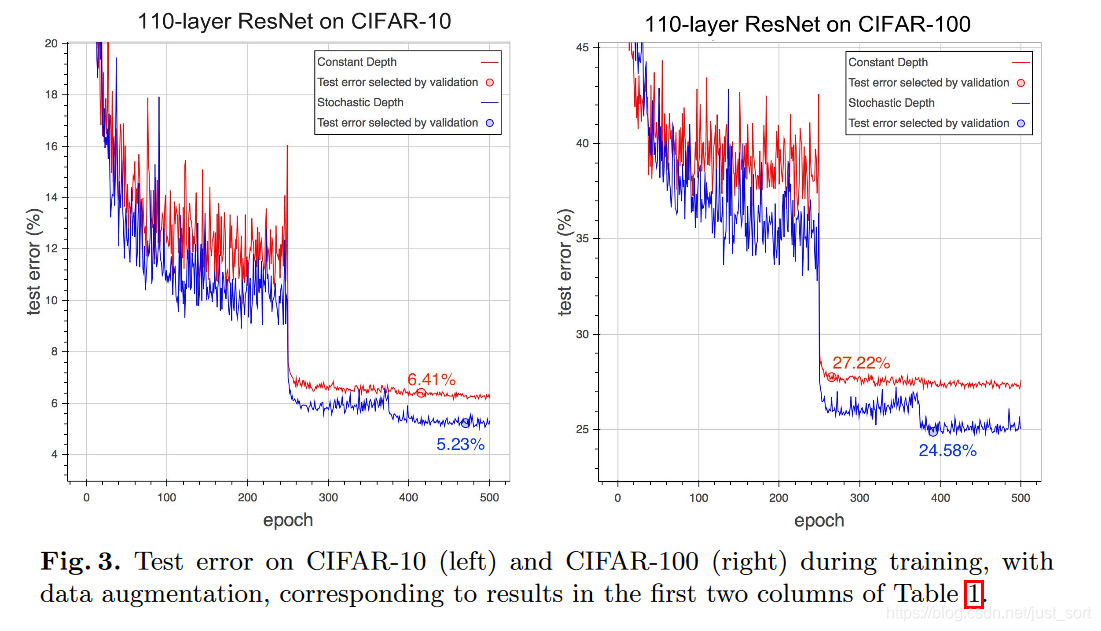
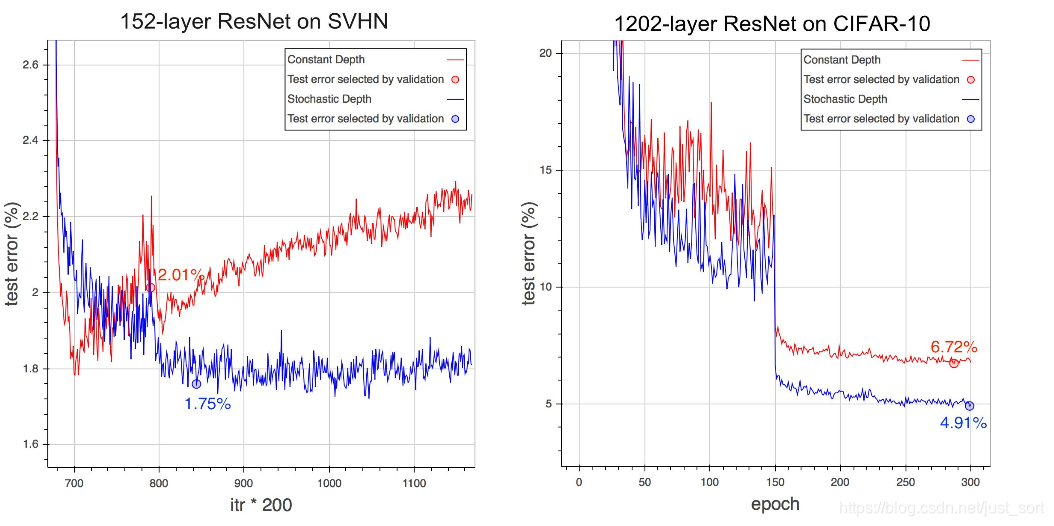
论文将ResNet的普通版和Stochastic_Depth版在CIFAR 10/100和SVHN做了实验。首先作者和其他当时的SOTA网络在CIFAR10和CIFAR100上的错误率做了一个对比，如Table1所示：

在这里插入图片描述

训练过程中的测试错误率曲线随着Epoch数的变化情况如下：

在这里插入图片描述

下面的Table2展示了在相同数据集上训练ResNet的训练时间，随机深度网络比原始的ResNet有25%左右的训练速度提升。

在这里插入图片描述

为什么随机深度网络有效？¶

从实验结果可以看到，随机深度网络的精度比ResNet更高，证明了其具有更好的泛化能力，这是为什么呢？论文中的解释是，不激活一部分残差模块事实上提现了一种模型融合的思想(和dropout解释一致)，由于训练时模型的深度随机，预测时模型的深度确定，实际是在测试时把不同深度的模型融合了起来。不过在查阅资料时我发现了另外一种解释，觉得也是有道理的，我贴一下截图。原始文章来自：https://zhuanlan.zhihu.com/p/31200098。

在这里插入图片描述

代码实现¶

随机深度网络中的将原始的残差模块替换为下面的带丢弃的单元即可，原始的可训练的代码见附录。

def residual_drop(x, input_shape, output_shape, strides=(1, 1)):
    global add_tables

    nb_filter = output_shape[0]
    conv = Convolution2D(nb_filter, 3, 3, subsample=strides,
                         border_mode="same", W_regularizer=l2(weight_decay))(x)
    conv = BatchNormalization(axis=1)(conv)
    conv = Activation("relu")(conv)
    conv = Convolution2D(nb_filter, 3, 3,
                         border_mode="same", W_regularizer=l2(weight_decay))(conv)
    conv = BatchNormalization(axis=1)(conv)

    if strides[0] >= 2:
        x = AveragePooling2D(strides)(x)

    if (output_shape[0] - input_shape[0]) > 0:
        pad_shape = (1,
                     output_shape[0] - input_shape[0],
                     output_shape[1],
                     output_shape[2])
        padding = K.zeros(pad_shape)
        padding = K.repeat_elements(padding, K.shape(x)[0], axis=0)
        x = Lambda(lambda y: K.concatenate([y, padding], axis=1),
                   output_shape=output_shape)(x)

    _death_rate = K.variable(death_rate)
    scale = K.ones_like(conv) - _death_rate
    conv = Lambda(lambda c: K.in_test_phase(scale * c, c),
                  output_shape=output_shape)(conv)

    out = merge([conv, x], mode="sum")
    out = Activation("relu")(out)

    gate = K.variable(1, dtype="uint8")
    add_tables += [{"death_rate": _death_rate, "gate": gate}]
    return Lambda(lambda tensors: K.switch(gate, tensors[0], tensors[1]),
                  output_shape=output_shape)([out, x])

后记¶

随机深度网络就讲到这里了，我下线了。。

附录¶

论文原文：https://arxiv.org/abs/1603.09382v1?utm_content=bufferbf6d7&utm_medium=social&utm_source=twitter.com&utm_campaign=buffer
Keras代码实现：https://github.com/dblN/stochastic_depth_keras

卷积神经网络学习路线往期文章¶

欢迎关注我的微信公众号GiantPandaCV，期待和你一起交流机器学习，深度学习，图像算法，优化技术，比赛及日常生活等。

图片.png

本文总阅读量次