跳转至

【GiantPandaCV导语】本文介绍了一种简单强力的VGG式网络结构，仅包含3x3卷积，BN层，Relu激活函数，通过重参数化提高其性能，准确率直逼其他SOTA网络（如RegNet和EfficientNet）。推理的时候因为可以通过融合分支，将模型变为单路结构，推理时间也能显著降低。

介绍

早期卷积网络结构主要是手工设计，通过不断堆叠卷积层以取得更好的效果（如AlexNet和VGG），而近些年来，为了提高网络性能，研究者基于NAS和手工也衍生出了很多复杂的结构，如：

  • 基于多分支结构设计，如残差网络add，Inception系列中的concat操作。多分支结构带来的问题是难以自定义，增加推理时间，增加显存消耗（因为需要保存各个分支的结果，直到add操作后，显存才会减少，后续会分析）

  • 一些网络结构组件，比如为轻量化网络设计的DepthwiseConv和ShuffleNet中的channel shuffle。这些操作会提高访存消耗，FLOPS看起来很低，但并不能反应实际推理速度。

新颖的组件固然能提升模型精度，但是复杂的结构会影响推理速度。因此直到现在，VGG和ResNet仍然被广泛应用。当然，其中一个巨大的挑战是如何提升VGG这种plain结构的精度。

选择VGG式网络的三个原因

速度快

现有的计算库（如CuDNN,Intel MKL）和硬件针对3x3卷积有深度的优化，相比其他卷积核，3x3卷积计算密度更高，更加有效。

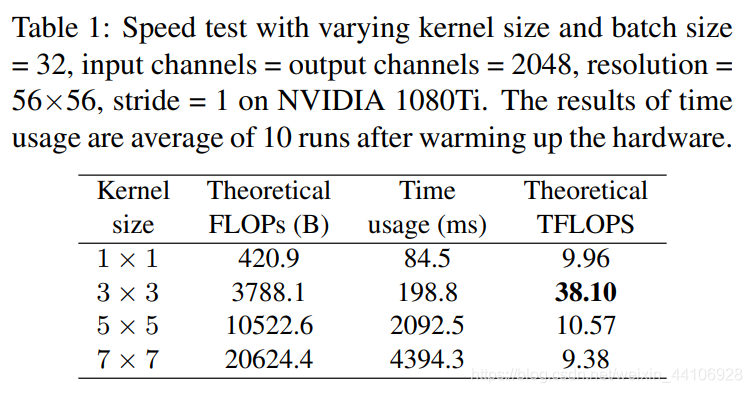
不同卷积核对应的FLOPS

比如VGG16的FLOPS比EfficientNetB3大8倍，但是VGG使用的都是3x3卷积，计算密度高，EfficientNet为了节约计算量和提高性能引入了DepthwiseConv，SE注意力，但是最终运行速度RepVGG要快1.8倍

节省显存

前面提过多分支结构很消耗显存的，因为各个分支的结果需要保存，直到最后一步融合（比如add），才能把各分支显存释放掉

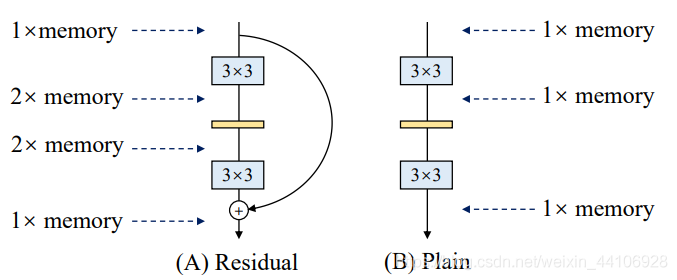
不同结构对显存的消耗

以残差块结构为例子，它有2个分支，其中主分支经过卷积层，假设前后张量维度相同，我们认为是一份显存消耗，另外一个旁路分支需要保存初始的输入结果，同样也是一份显存消耗，这样在运行的时候是占用了两份显存，直到最后一步将两个分支结果Add，显存才恢复成一份。而Plain结构只有一个主分支，所以其显存占用一直是一份。

灵活

多分支结构会引入网络结构的约束，比如Resnet的残差结构要求输入和卷积出来的张量维度要一致（这样才能相加），这种约束导致网络不易延伸拓展，也一定程度限制了通道剪枝。对应的单路结构就比较友好，剪枝后也能得到很好的加速比。

提升VGG性能——从多分支开始

VGG这种单路网络的缺点就是性能不好，72%的准确率放在当下来看已经是很落后了。受Resnet的残差结构启发，我们引入了残差分支和1x1卷积分支，为了后续重参数化成单路结构，我们调整了分支放置的位置，没有进行跨层连接，而是直接连了过去。

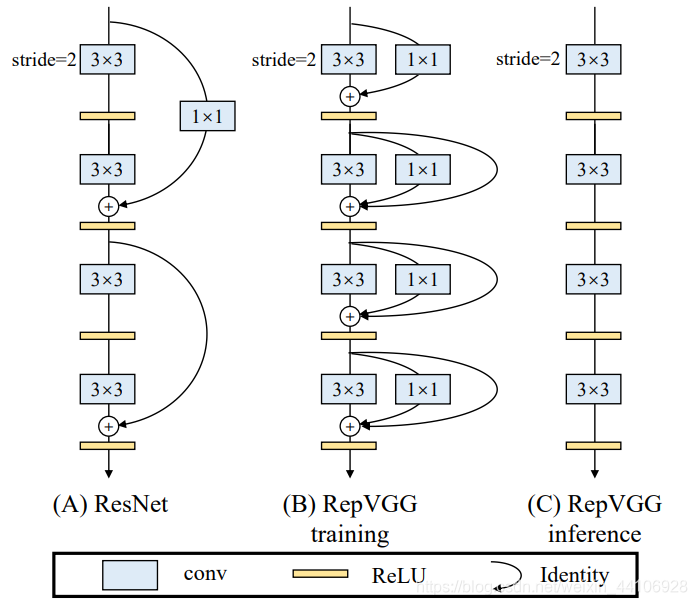
RepVGG结构总览

相当于一个Block内所作的计算为

Out = F(X)+G(X)+X \\ F(X)表示3*3卷积 \\ G(X)表示1*1卷积

后续的消融实验了证明了这两个分支对性能提升的重要性

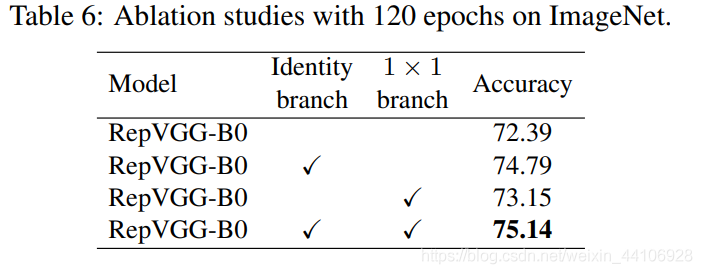
多分支消融实验

其中Idendity分支（即残差连接）提升尤为明显，1x1卷积分支也能提供近一个点的贡献。两个分支合并能贡献3个点的提升。

提升推理速度——多分支融合技术

卷积+BN 融合

RepVGG里面大量使用卷积层和BN层，这里首先将两者合并起来，能提高推理速度

卷积层公式为

Conv(x) = W(x)+b

而BN层公式为

BN(x) = \gamma*\frac{(x-mean)}{\sqrt{var}}+\beta

然后我们将卷积层结果带入到BN公式中

BN(Conv(x)) = \gamma*\frac{W(x)+b-mean}{\sqrt{var}}+\beta

进一步化简为

BN(Conv(x)) = \frac{\gamma*W(x)}{\sqrt{var}}+(\frac{\gamma*(b-mean)}{\sqrt{var}}+\beta)

看到这个公式是不是很熟悉？这其实就是一个卷积层，只不过权重考虑了BN的参数 我们令

W_{fused}=\frac{\gamma*W}{\sqrt{var}} \\ B_{fused}=\frac{\gamma*(b-mean)}{\sqrt{var}}+\beta

最终融合的结果就是

BN(Conv(x)) = W_{fused}(x)+B_{fused}

相关代码

    def _fuse_bn_tensor(self, branch):
        if branch is None:
            return 0, 0
        if isinstance(branch, nn.Sequential):
            kernel = branch.conv.weight
            running_mean = branch.bn.running_mean
            running_var = branch.bn.running_var
            gamma = branch.bn.weight
            beta = branch.bn.bias
            eps = branch.bn.eps
        else:
            ...
        std = (running_var + eps).sqrt()
        t = (gamma / std).reshape(-1, 1, 1, 1)
        return kernel * t, beta - running_mean * gamma / std

这里跟公式不一样的是融合bias的，RepVGG中卷积层没有使用Bias，我们把前面公式推导中的b去掉即可。

卷积分支融合

3x3卷积和1x1卷积融合

为了方便理解，这里仅考虑stride=1且卷积前后特征图大小不变的情况

首先我们看下1x1卷积

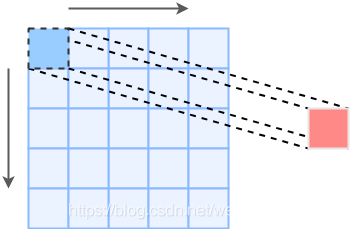
1x1卷积

这里1x1卷积不需要padding，就能保证特征图大小前后一致，下面我们再看看3x3卷积

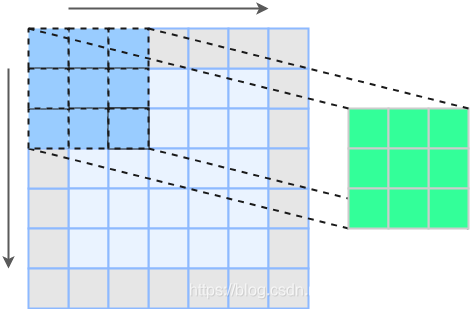
3x3卷积

为了保证特征图大小不变，我们需要在原特征图上padding一圈（图中灰色部分表示padding）

我们观察下3x3卷积核中间的那个核，会惊奇的发现它卷积的路径就是前面1x1卷积的路径

3x3卷积中心

一个很自然的想法是，把1x1卷积核加在3x3卷积核中间，就能完成卷积分支融合

下面是融合之后的示例图

1x1卷积和3x3卷积融合

identity分支等效特殊权重卷积层

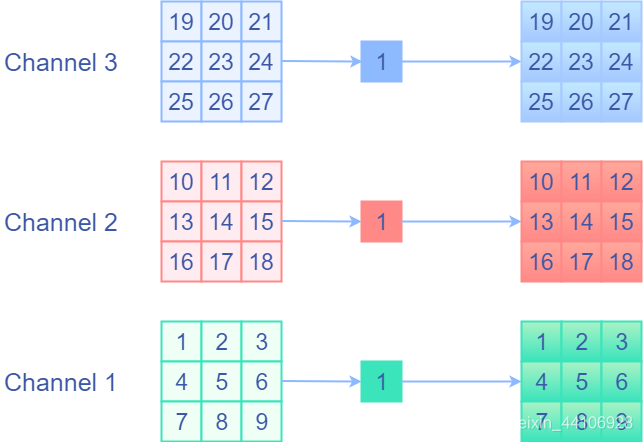
现在我们还遗留了一个identity分支，说白了就是Elementwise相加，每个通道中每个元素对应相加。那么现在的问题是将identity分支用一个卷积层表示，这样才有可能融合。identity前后值不变，那么我会想到是用权重等于1的卷积核，并分开通道进行卷积，即1x1的，权重固定为1的Depthwise卷积。这样相当于单独对每个通道的每个元素乘1，然后再输出来，这就是我们想要的identity操作！下面是一个示意图 1x1Depthwise卷积等效

我们可以用一段代码进行验证，下面是基于oneflow框架的代码：

import oneflow as flow 
import oneflow.typing as tp 
import numpy as np 


@flow.global_function()
def test_identity(x: tp.Numpy.Placeholder(shape=(1, 3, 3, 3)))->tp.Numpy: 
    in_channels = x.shape[1]
    out_channels = in_channels
    groups = in_channels 
    kernel_size = 1
    weight = flow.get_variable(
        shape=(out_channels, in_channels//groups, kernel_size, kernel_size), 
        initializer=flow.ones_initializer(), 
        name="identity_weight"
    )
    return flow.nn.conv2d(x, filters=weight, padding=(0, 0, 0, 0), strides=1, groups=groups)

x = np.array([[[[1, 2, 3], 
                [4, 5, 6], 
                [7, 8, 9]], 
               [[10, 11, 12], 
                [13, 14, 15], 
                [16, 17, 18]], 
               [[19, 20, 21], 
                [22, 23, 24], 
                [25, 26, 27]]]]).astype(np.float32)
out = test_identity(x)
print("Output is: ", out)

我们设置卷积层输入输出通道相等，分组数等于输入通道数（这样就是Depthwise卷积了），卷积核大小和步长都设置为1

然后构造一组形状为（1，3，3，3）NCHW格式的数据 验证下结果

Output is:  [[[[ 1.  2.  3.]
               [ 4.  5.  6.]
               [ 7.  8.  9.]]

              [[10. 11. 12.]
               [13. 14. 15.]
               [16. 17. 18.]]

              [[19. 20. 21.]
               [22. 23. 24.]
               [25. 26. 27.]]]]

这里我们初步达到了我们的目的，但是新的问题产生了，我们的3x3和1x1分支都不是Depthwise卷积，现在也是不能融合进去的，我们需要把Depthwise卷积以普通卷积的形式表达出来。

因为普通卷积输出是将各个通道结果相加，那么自然而然想到，我们只要将当前通道对应的卷积权重设置为1，而其他通道权重设置为0，不就等价Depthwise卷积了！ 下面是一个示意图

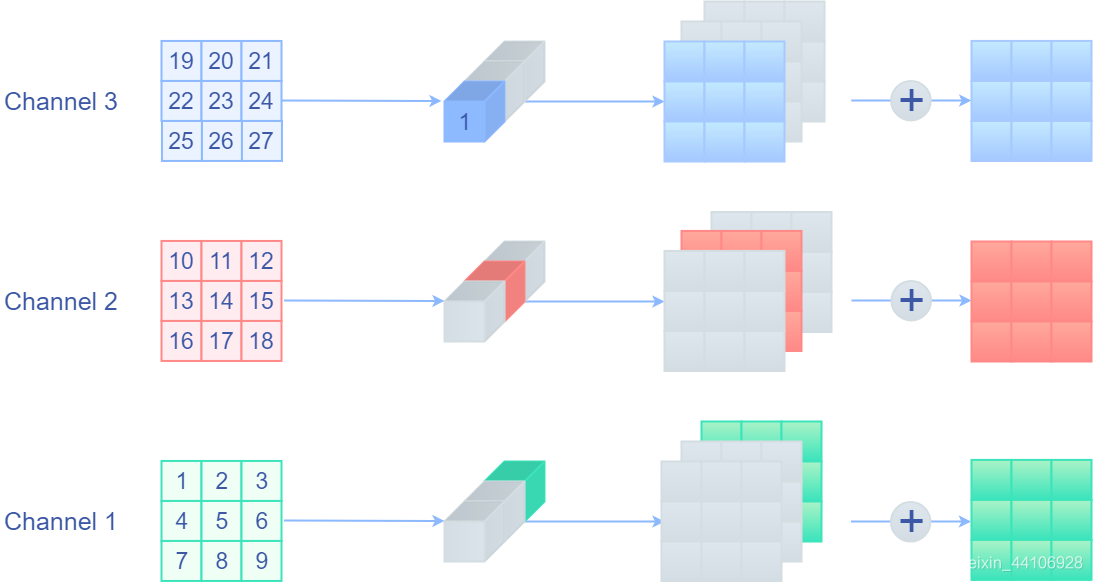
普通1x1卷积等价Identity

其中灰色的地方均表示0

到了这里，我们也能用普通1x1卷积来等效Identity分支了，不过先别急，它还有个重要的性质，我们将卷积核都展开，会得到下面的图

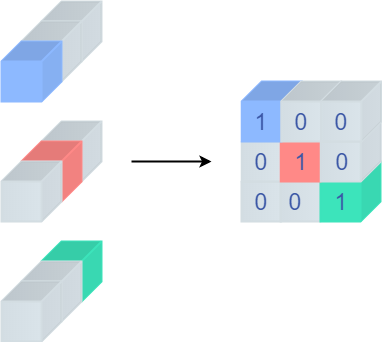
Identity卷积核展开

很神奇的是，展开来得到的是一个单位矩阵！这个性质十分重要，划重点，等等融合分支的时候会用到。

下面我们来仔细看下代码

首先是将1x1卷积核padding一圈0，让他变成“3x3卷积核”

 def _pad_1x1_to_3x3_tensor(self, kernel1x1):
     if kernel1x1 is None:
         return 0
     else:
         return torch.nn.functional.pad(kernel1x1, [1, 1, 1, 1])

然后是具体融合了，主要方法还是前面的 _fuse_bn_tensor

    def _fuse_bn_tensor(self, branch):
        if branch is None:
            return 0, 0
        if isinstance(branch, nn.Sequential):
            # 3x3卷积和1x1卷积分支
            kernel = branch.conv.weight
            running_mean = branch.bn.running_mean
            running_var = branch.bn.running_var
            gamma = branch.bn.weight
            beta = branch.bn.bias
            eps = branch.bn.eps
        else:
            assert isinstance(branch, nn.BatchNorm2d)
            if not hasattr(self, 'id_tensor'):
                input_dim = self.in_channels // self.groups
                kernel_value = np.zeros((self.in_channels, input_dim, 3, 3), dtype=np.float32)
                for i in range(self.in_channels):
                    kernel_value[i, i % input_dim, 1, 1] = 1
                self.id_tensor = torch.from_numpy(kernel_value).to(branch.weight.device)
            kernel = self.id_tensor
            running_mean = branch.running_mean
            running_var = branch.running_var
            gamma = branch.weight
            beta = branch.bias
            eps = branch.eps
        std = (running_var + eps).sqrt()
        t = (gamma / std).reshape(-1, 1, 1, 1)
        return kernel * t, beta - running_mean * gamma / std

因为1x1卷积被padding成了3x3卷积，所以它和3x3卷积融合BN采用的是同一套逻辑。 else分支下则是Identity分支融合的逻辑，由于后续网络会引入分组，所以这里用groups计算了下卷积核对应的输入通道，然后就是一个for循环给卷积核赋值1。

这里可能不太好理解，首先我们假设不分组，则 input_dim=in_channels，循环里的赋值第二个维度是i % input_dim，但是i是一个循环的变量，他是小于input_dim的，所以 i%input_dim其实就是i。用更简洁的代码就是

for i in range(self.in_channels):
    kernel_value[i, i, 1, 1] = 1

这里就是用到了前面推导Identity分支，其卷积核等价于单位矩阵的这个特性，对第(i, i)个元素赋值为1。后续则是将Identity分支上的BN参数给赋值过去。类似的，我们也可以推导分组的融合逻辑。

最后就是将这3个分支转换的结果加在一起

def get_equivalent_kernel_bias(self):
    kernel3x3, bias3x3 = self._fuse_bn_tensor(self.rbr_dense) # self.rbr_dense是3x3卷积分支
    kernel1x1, bias1x1 = self._fuse_bn_tensor(self.rbr_1x1) # self.rbr_1x1是1x1卷积分支
    kernelid, biasid = self._fuse_bn_tensor(self.rbr_identity) # self.rbr_identity是Identity分支
    return kernel3x3 + self._pad_1x1_to_3x3_tensor(kernel1x1) + kernelid, bias3x3 + bias1x1 + biasid

至此我们就完全搞懂融合的全部原理了

实验结果

作者提出了A和B系列两种模型，其区别是卷积块堆叠设置，并设立了两个参数a，b来控制通道数

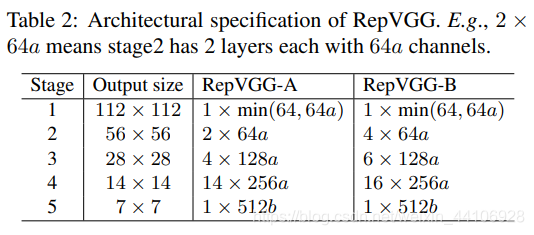
RepVGG架构

具体配置

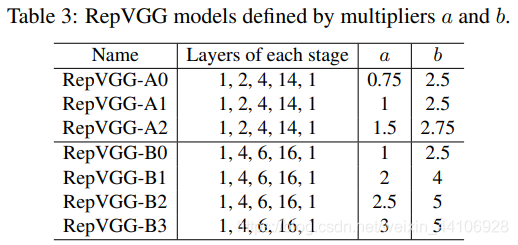
可以看到参数设置的也是很正常的数字，没有很花里胡哨的超参调整

精度对比

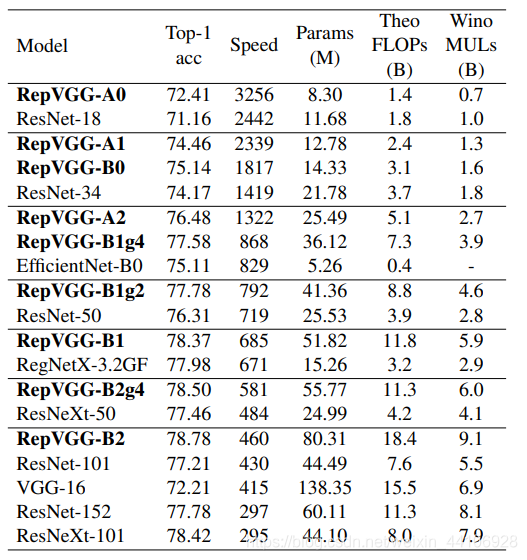
在普通数据增广下，性能能直逼一些SOTA模型

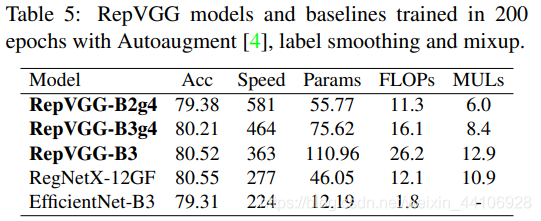
精度对比2

加上了AutoAugment，标签平滑，MixUp这些Trick，性能也能和RegNet，EfficientNet对齐。

总结

RepVGG在我看来真的是一个很棒的BackBone工作，它避免了花里胡哨的模块设计，NAS搜索，仅仅靠简单的手工设计和重参数化达到了SOTA结果。作者丁霄汉其实已经介绍过这篇论文 RepVGG：极简架构，SOTA性能，让VGG式模型再次伟大(https://zhuanlan.zhihu.com/p/344324470)，他也是ACNet的作者，将1x3和3x1卷积核融到了3x3卷积，想必RepVGG也是这一系列工作的延申。

我最近也是拿 OneFlow 框架对其进行复现，设置了以下参数

  • epoch 提升到160
  • labelsmooth 0.1
  • Warmup Epoch 5
  • Momentum 0.9

这样就可以很轻松的达到比论文稍好一点的结果

  • RepVGGA0 72.6
  • RepVGGA1 74.9
  • RepVGGA2 76.51
  • RepVGGB0 75.4

而且训练速度非常的快。RepVGGA0在四卡batchsize=256情况下，睡一觉第二天就能出结果。并且整个网络就是卷积层，BN层，Relu，十分适合部署，具体可参考 基于TensorRT量化部署RepVGG模型(https://mp.weixin.qq.com/s/9GPQrvxvxtlYYGPVIg3J0Q)。很期待作者后续的工作，近期可以关注下即将放出的ACNet2。

欢迎关注GiantPandaCV, 在这里你将看到独家的深度学习分享，坚持原创，每天分享我们学习到的新鲜知识。( • ̀ω•́ )✧

有对文章相关的问题，或者想要加入交流群，欢迎添加BBuf微信：

二维码

为了方便读者获取资料以及我们公众号的作者发布一些Github工程的更新，我们成立了一个QQ群，二维码如下，感兴趣可以加入。

公众号QQ交流群

本文总阅读量次