[toc]

【写在前面】¶

最近拜读了丁霄汉大神的一系列重参数的论文，觉得这个思想真的很妙。能够在将所有的cost都放在训练过程中，在测试的时候能够在所有的网络参数和计算量都进行缩减。目前网上也有部分对这些论文进行了解析，为了能够让更多读者进一步、深层的理解重参数的思想，本文将会结合代码，近几年重参数的论文进行详细的解析。

个人理解，重参数其实就是在测试的时候对训练的网络结构进行压缩。比如三个并联的卷积（kernel size相同）结果的和，其实就等于用求和之后的卷积核进行一次卷积的结果。所以，在训练的时候可以用三个卷积来提高模型的学习能力，但是在测试部署的时候，可以无损压缩为一次卷积，从而减少参数量和计算量。

【复现框架】¶

https://github.com/xmu-xiaoma666/External-Attention-pytorch

（欢迎大家star、fork该工作；如果有任何问题，也欢迎大家在issue中提出）

【先验知识】¶

首先向各位读者介绍一下卷积的一些基本性质，这几篇论文所提出的重参数操作，都是基于卷积的这几个性质。

一个普通的卷积操作可以被定义成下面的公式：

$O=I*F+REP(b)$

其中， $*$ 为卷积操作， $O \in \mathbb{R}^{D \times H' \times W'}$ 为输出特征， $I \in \mathbb{R}^{C \times H \times W}$ 为输入特征， $F \in \mathbb{R}^{D \times C \times K \times K}$ 为卷积核， $b \in \mathbb{R}^{D}$ 为偏置项， $Rep(b) \in \mathbb{R}^{D \times H' \times W'}$ 表示广播后的偏置项。

卷积操作具有以下两个性质：

1）同质性（homogeneity）¶

$I*(pF)=p(I*F), \forall p \in \mathbb{R}$

这个性质的意思是，一个常数与卷积核相乘之后的结果与特征进行卷积=一个常数乘上卷积之后的结果。

2）可加性（additivity）¶

$I*F^{(1)}+I*F^{(2)}=I*(F^{(1)}+F^{(2)})$

这个性质的意思是，两个并联的卷积结果相加，等于将这两个卷积核相加之后之后在进行卷积

1.ICCV2019-ACNet¶

1.1. 论文地址¶

ACNet: Strengthening the Kernel Skeletons for Powerful CNN via Asymmetric Convolution Blocks

论文地址：https://arxiv.org/abs/1908.03930

1.2. 网络框架¶

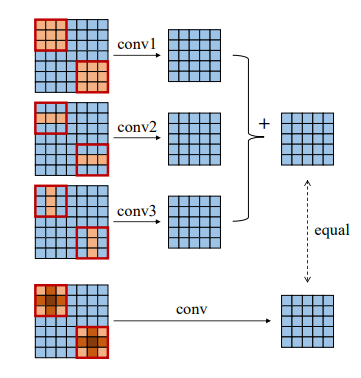
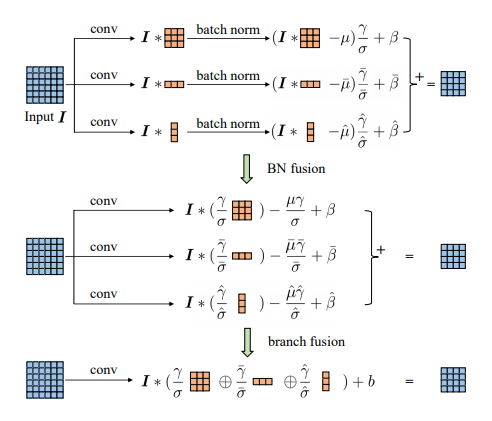
1.3. 原理解释¶

这篇文章做的主要工作如“网络框架”中的展示的那样：将并联的三个卷积（1x3、3x1、3x3）转换成一个卷积（3x3）。

首先，考虑不带BatchNorm的情况：¶

将1x3和3x1的卷积核转换到3x3的卷积核，只需要在水平和竖直方向分别用0padding成3x3的大小即可，然后将三个卷积核（1x3、3x1、3x3）相加进行卷积，就相当于是用三个卷积核分别对feature map卷积后再相加。

然后，考虑如何将BatchNorm融合到卷积核中：¶

卷积操作如下：

$O=I*F+REP(b)$

BatchNorm操作如下：

$BN(x)=\gamma\frac{(x-mean)}{\sqrt{var}}+\beta$

将卷积带入到BatchNorm就如：

$BN(Conv(x))=\gamma\frac{(I*F+REP(b)-mean)}{\sqrt{var}}+\beta$

化简得到：

$BN(Conv(x))=I*(\frac{F\gamma}{\sqrt{var}})+\frac{\gamma(REP(b)-mean)}{\sqrt{var}}+\beta$

因此新卷积核的weight和bias为：

$F_{new}=\frac{F\gamma}{\sqrt{var}} \\ REP(b)=\frac{\gamma(REP(b)-mean)}{\sqrt{var}}+\beta$

最后，考虑多分支的带BN的结构融合：¶

第一步，我们将BN层的参数融合到卷积核中

第二步，将BN层的参数融合到卷积核之后，原来带BN层的结构就变成了不带BN层的结构，我们将三个新卷积核相加之后，就得到了融合的卷积核。

1.4. 代码调用¶

from rep.acnet import ACNet
import torch
from torch import nn

input=torch.randn(50,512,49,49)
acnet=ACNet(512,512)
acnet.eval()
out=acnet(input)
acnet._switch_to_deploy()
out2=acnet(input)
print('difference:')
print(((out2-out)**2).sum())

2. CVPR2021-RepVGG¶

2.1. 论文地址¶

RepVGG: Making VGG-style ConvNets Great Again

论文地址：https://arxiv.org/abs/2101.03697

2.2. 网络框架¶

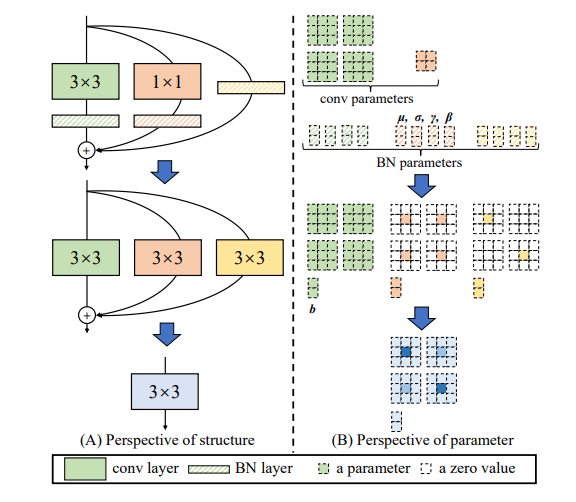
2.3. 原理解释¶

这篇论文是的核心是将并联的带BN的3x3卷积核,1x1卷积核和残差结构转换为一个3x3的卷积核。

首先，带BN的1x1卷积核和带BN的3x3卷积核融合成一个3x3的卷积核，这个操作和第一篇文章ACNet的转换方式非常相似，就是将1x1 的卷积核padding成3x3后，在进行和ACNet相同的操作。

现在的问题是，怎么把残差结构也变成3x3的卷积。残差结构可以其实就是一个value为1的1x1的Depthwise卷积。如果能把Depthwise卷积转换成正常的卷积，那么这个问题也就迎刃而解了。下面这张图形象的展示了如果把Depthwise卷积转换成正常卷积：

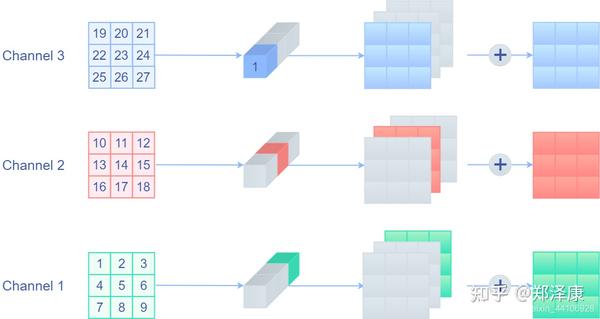
（来自：https://zhuanlan.zhihu.com/p/352239591）

其实就是将对应需要操作的通道赋值为1，其他赋值为0。

输入通道为c，输出通道为c，把这里的参数矩阵比作cxc的矩阵，那么深度可分离矩阵就是一个单位矩阵（对角位置全部为1，其他全部为0）

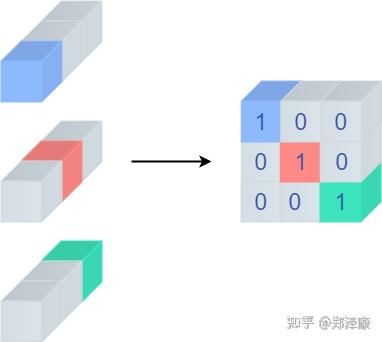
（来自：https://zhuanlan.zhihu.com/p/352239591）

这样一来，残差结构也能转换成1x1的卷积了，然后与3x3的卷积用上面的方式进行合并，就得到了RepVGG的重参数结构

2.4. 代码调用¶

from rep.repvgg import RepBlock
import torch

input=torch.randn(50,512,49,49)
repblock=RepBlock(512,512)
repblock.eval()
out=repblock(input)
repblock._switch_to_deploy()
out2=repblock(input)
print('difference between vgg and repvgg')
print(((out2-out)**2).sum())

3. CVPR2021-Diverse Branch Block¶

3.1. 论文地址¶

Diverse Branch Block: Building a Convolution as an Inception-like Unit

论文地址：https://arxiv.org/abs/2103.13425

3.2. 网络框架¶

3.3. 原理解释¶

像Inception一样的多分支结构可以增加模型的表达能力，提高性能，但是也会带来额外的参数和显存使用。因此，本文提出了一个方法，在训练时采用多分支的结构，在测试和部署的时候将多分支的结构模型转换成一个单一分支的模型，从而模型在测试的时候就能够“免费”享用多分支结构带来的性能提升。但是怎么把多分支结构无损压缩成一个单分支的结构呢，这就是这篇文章的贡献点所在。

3.3.1. Transform I:Conv+BN->BN¶

这部分的原理在ACNet的解析中已经详细解释了，代码实现如下：

def transI_conv_bn(conv, bn):

    std = (bn.running_var + bn.eps).sqrt()
    gamma=bn.weight

    weight=conv.weight*((gamma/std).reshape(-1, 1, 1, 1))
    if(conv.bias is not None):
        bias=gamma/std*conv.bias-gamma/std*bn.running_mean+bn.bias
    else:
        bias=bn.bias-gamma/std*bn.running_mean
    return weight,bias

3.3.2. Transform II:并联Conv->Conv¶

这部分的原理就是【先验知识】部分的可加性，代码实现如下：

def transII_conv_branch(conv1, conv2):
    weight=conv1.weight.data+conv2.weight.data
    bias=conv1.bias.data+conv2.bias.data
    return weight,bias

3.3.3 Transform III:1x1Conv + 3x3Conv->3x3Conv¶

1x1的卷积其实并没有在空间上对feature map进行交互操作（或者说都只是乘了相同的数），所以1x1的Conv其实就是一个全连接层。所以，本质上，我们可以直接后面接着的3x3的卷积进行这个1x1的卷积操作，得到的新的卷积核，就可以是融合之后的卷积核。（可能讲的不是非常清楚，详细解释可以参考这篇文章：https://zhuanlan.zhihu.com/p/360939086）

代码实现如下：

def transIII_conv_sequential(conv1, conv2):
    weight=F.conv2d(conv2.weight.data,conv1.weight.data.permute(1,0,2,3))
    return weight

3.3.4 Transform IV:Concat Conv->Conv¶

将多个卷积之后的结果进行concat，其实就是将多个卷积核权重在输出通道维度上进行拼接即可，代码实现如下：

def transIV_conv_concat(conv1, conv2):
    print(conv1.bias.data.shape)
    print(conv2.bias.data.shape)
    weight=torch.cat([conv1.weight.data,conv2.weight.data],0)
    bias=torch.cat([conv1.bias.data,conv2.bias.data],0)
    return weight,bias

3.3.5 Transform V:AvgPooling->Conv¶

AvgPool就是将感受野的值求平均，那么转换成卷积就是卷积核中每个值的value都等于1/卷积核大小，代码实现如下：

def transV_avg(channel,kernel):
    conv=nn.Conv2d(channel,channel,kernel,bias=False)
    conv.weight.data[:]=0
    for i in range(channel):
        conv.weight.data[i,i,:,:]=1/(kernel*kernel)
    return conv

3.3.6 Transform VI:1x1Conv+1x3Conv+3x1Conv(并联)->Conv¶

这个操作其实就是ACNet的思想，详情可以见上面ACNet的解析，代码实现如下：

def transVI_conv_scale(conv1, conv2, conv3):
    weight=F.pad(conv1.weight.data,(1,1,1,1))+F.pad(conv2.weight.data,(0,0,1,1))+F.pad(conv3.weight.data,(1,1,0,0))
    bias=conv1.bias.data+conv2.bias.data+conv3.bias.data
    return weight,bias

3.4. 代码调用¶

3.4.1. Transform I:Conv+BN->BN¶

from rep.ddb import transI_conv_bn
import torch
from torch import nn
from torch.nn import functional as F

input=torch.randn(1,64,7,7)
#conv+bn
conv1=nn.Conv2d(64,64,3,padding=1)
bn1=nn.BatchNorm2d(64)
bn1.eval()
out1=bn1(conv1(input))

#conv_fuse
conv_fuse=nn.Conv2d(64,64,3,padding=1)
conv_fuse.weight.data,conv_fuse.bias.data=transI_conv_bn(conv1,bn1)
out2=conv_fuse(input)

print("difference:",((out2-out1)**2).sum().item())

3.4.2. Transform II:并联Conv->Conv¶

from rep.ddb import transII_conv_branch
import torch
from torch import nn
from torch.nn import functional as F

input=torch.randn(1,64,7,7)

#conv+conv
conv1=nn.Conv2d(64,64,3,padding=1)
conv2=nn.Conv2d(64,64,3,padding=1)
out1=conv1(input)+conv2(input)

#conv_fuse
conv_fuse=nn.Conv2d(64,64,3,padding=1)
conv_fuse.weight.data,conv_fuse.bias.data=transII_conv_branch(conv1,conv2)
out2=conv_fuse(input)

print("difference:",((out2-out1)**2).sum().item())

3.4.3 Transform III:1x1Conv + 3x3Conv->3x3Conv¶

from rep.ddb import transIII_conv_sequential
import torch
from torch import nn
from torch.nn import functional as F

input=torch.randn(1,64,7,7)

#conv+conv
conv1=nn.Conv2d(64,64,1,padding=0,bias=False)
conv2=nn.Conv2d(64,64,3,padding=1,bias=False)
out1=conv2(conv1(input))


#conv_fuse
conv_fuse=nn.Conv2d(64,64,3,padding=1,bias=False)
conv_fuse.weight.data=transIII_conv_sequential(conv1,conv2)
out2=conv_fuse(input)

print("difference:",((out2-out1)**2).sum().item())

3.4.4 Transform IV:Concat Conv->Conv¶

from rep.ddb import transIV_conv_concat
import torch
from torch import nn
from torch.nn import functional as F

input=torch.randn(1,64,7,7)

#conv+conv
conv1=nn.Conv2d(64,32,3,padding=1)
conv2=nn.Conv2d(64,32,3,padding=1)
out1=torch.cat([conv1(input),conv2(input)],dim=1)

#conv_fuse
conv_fuse=nn.Conv2d(64,64,3,padding=1)
conv_fuse.weight.data,conv_fuse.bias.data=transIV_conv_concat(conv1,conv2)
out2=conv_fuse(input)

print("difference:",((out2-out1)**2).sum().item())

3.4.5 Transform V:AvgPooling->Conv¶

from rep.ddb import transV_avg
import torch
from torch import nn
from torch.nn import functional as F

input=torch.randn(1,64,7,7)

avg=nn.AvgPool2d(kernel_size=3,stride=1)
out1=avg(input)

conv=transV_avg(64,3)
out2=conv(input)

print("difference:",((out2-out1)**2).sum().item())

3.4.6 Transform VI:1x1Conv+1x3Conv+3x1Conv(并联)->Conv¶

from rep.ddb import transVI_conv_scale
import torch
from torch import nn
from torch.nn import functional as F

input=torch.randn(1,64,7,7)

#conv+conv
conv1x1=nn.Conv2d(64,64,1)
conv1x3=nn.Conv2d(64,64,(1,3),padding=(0,1))
conv3x1=nn.Conv2d(64,64,(3,1),padding=(1,0))
out1=conv1x1(input)+conv1x3(input)+conv3x1(input)

#conv_fuse
conv_fuse=nn.Conv2d(64,64,3,padding=1)
conv_fuse.weight.data,conv_fuse.bias.data=transVI_conv_scale(conv1x1,conv1x3,conv3x1)
out2=conv_fuse(input)

print("difference:",((out2-out1)**2).sum().item())

本文总阅读量次