浅谈LabelSmooth的两种实现以及推导_蒋

【GiantPandaCV导语】因为最近跑VIT的实验，所以有用到timm的一些配置，在mixup的实现里面发现labelsmooth的实现是按照最基本的方法来的，与很多pytorch的实现略有不同，所以简单做了一个推导。

一、交叉熵损失(CrossEntropyLoss)¶

先简单讲一下交叉熵损失，也是我们做分类任务里面最常用的一种损失，公式如下：

这里的 $x_{i}$表示的是模型输出的logits后经过softmax的结果，shape为 $(N, M)$， $y_{i}$表示的是对应的label，经常用onehot来表示，pytorch版本可以使用scalar表示，shape为 $(N, )$，这里 $N$表示为batchsize， $M$表示为向量长度。

可以简单拆解为如下：

• log_softmax

这个很简单，就是做softmax后取对数，公式如下：

• NLLloss

这个玩意的全程叫做negative log-likelihood(负对数似然损失), 简单解释下: 假设需要求解一个分布 $ p_{real}(x) $ ,由于未知其表达式，所以先定义一个分布 $p_{fake}(x;\theta)$，通过 $\theta$ 来使得 $p_{fake}$靠近 $p_{real}$的分布。这里采用最大似然估计来进行求解， $L=\prod_{i}^np_{fake}(x_{i};\theta)$ ，不断的更新参数 $\theta$使得 来自 $p_{real}$的样本 $[x_{1}, x_{2}, ... , x_{n}]$ 在 $p_{fake}$中的概率越来越高。但是有个问题，连乘对于求导不友好，计算也过于复杂，所以可以对其取对数，有

最大化对数似然函数就等效于最小化负对数似然函数，所以加个负号，公式如下：

由于求loss的时候，采用的是onehot形式，除去当前类别为1其余都为0，所以有：

这个形式就和交叉熵形式一致，所以NLLLoss也叫CrossEntropyLoss。

二、LabelSmooth¶

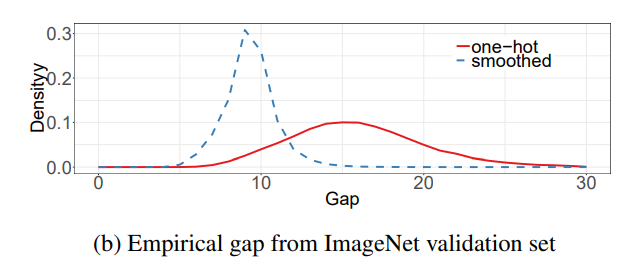
由于Softmax会存在一个问题，就是Over Confidence，会使得模型对于弱项的照顾很少。LabelSmooth的作用就是为了降低Softmax所带来的的高Confidence的影响，让模型略微关注到低概率分布的权重。这样做也会有点影响，最终预测的时候，模型输出的置信度会稍微低一些，需要比较细致的阈值过滤。

假设 $\varepsilon=0.1$，表示对标签进行平滑的数值，那么就有

这里 classes表示类别数量， target表示当前的类别，带有labelsmooth的CELoss就变成了：

相比原始的CELoss，LabelSmoothCELoss则是每一项都会参与到loss计算。

三、公式推导¶

# labelsmooth 
import torch 
import torch.nn as nn 
import torch.nn.functional as F 


class LabelSmoothingCrossEntropy(nn.Module):
    """
    NLL loss with label smoothing.
    """
    def __init__(self, smoothing=0.1):
        """
        Constructor for the LabelSmoothing module.
        :param smoothing: label smoothing factor
        """
        super(LabelSmoothingCrossEntropy, self).__init__()
        assert smoothing < 1.0
        self.smoothing = smoothing
        self.confidence = 1. - smoothing

    def forward(self, x, target):
        logprobs = F.log_softmax(x, dim=-1)
        nll_loss = -logprobs.gather(dim=-1, index=target.unsqueeze(1))
        nll_loss = nll_loss.squeeze(1)
        smooth_loss = -logprobs.mean(dim=-1)
        loss = self.confidence * nll_loss + self.smoothing * smooth_loss
        return loss.mean()

可以看到这个code的实现和公式有点出入，第一部分是self.confidence * nll_loss, 第二部分是self.smoothing * smooth_loss。我们将其展开为：

假设 k为target，那么对于onehot来说除了 $x_k=1$以外均为0，所以有：

进一步有组合 $x_{k}$项：

最后可以写成矩阵点乘的形式：

我们表示 $\left[ \frac{\varepsilon}{n}, ..., (1 - \varepsilon +\frac{\varepsilon}{n}）,..., \frac{\varepsilon}{n} \right]$为LabelSmooth后的标签 $y(x_{i})$，和第二节中的设定对齐，所以得到的Loss就是原本的表达式：

与之对应的timm中的mixup部分的LabelSmoothCELoss代码如下：

def one_hot(x, num_classes, on_value=1., off_value=0., device='cuda'):
    x = x.long().view(-1, 1)
    return torch.full((x.size()[0], num_classes), off_value, device=device).scatter_(1, x, on_value)


def mixup_target(target, num_classes, lam=1., smoothing=0.0, device='cuda'):
    off_value = smoothing / num_classes
    on_value = 1. - smoothing + off_value
    y1 = one_hot(target, num_classes, on_value=on_value, off_value=off_value, device=device)
    y2 = one_hot(target.flip(0), num_classes, on_value=on_value, off_value=off_value, device=device)
    return y1 * lam + y2 * (1. - lam)

四，总结¶

LabelSmooth可以用来标签平滑，从公示推导方面来讲，也可以充当正则的作用，尤其是针对难分类别的情况下，效果会表现更好一些。