简介¶

在该工作中，我们提出了一种名为ACON(Activate Or Not)激活函数。此外，我们发现由NAS搜索得到的Swish函数，是我们常用的ReLU激活函数的平滑形式。我们将该形式推广到ReLU函数的其他变体（Leaky-ReLU, PReLU等）。最后我们提出了一个meta-ACON激活函数和其设计空间，它可以自适应的选择是否激活神经元，通过替换原网络的激活层，能提升1-2个点的网络精度（ResNet-152)。

论文地址：Activate or Not: Learning Customized Activation(https://arxiv.org/abs/2009.04759)

代码地址：nmaac/ACON.pytorch(https://github.com/nmaac/ACON.pytorch)

Smooth Maximum¶

我们常用的ReLU激活函数本质是一个MAX函数，其公式如下

而MAX函数的平滑，可微分变体我们称为Smooth Maximum，其公式如下

其中 $\beta$ 是一个平滑因子，当 $\beta$ 趋近于无穷大时，Smooth Maximum就变为标准的MAX函数，而当 $\beta$ 为0时，Smooth Maximum就是一个算术平均的操作

这里我们只考虑Smooth Maximum只有两个输入量的情况，于是有以下公式

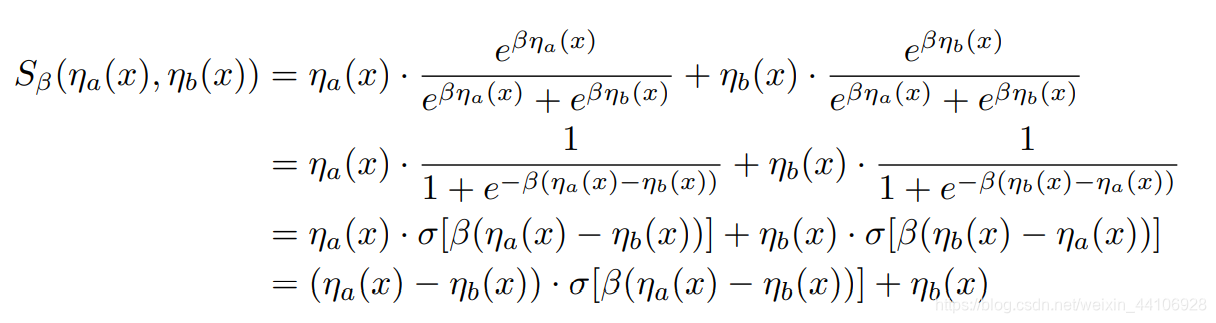
其中 $\sigma$ 表示 sigmoid函数

笔者写了一段关于Smooth Maximum的代码

import numpy as np
import matplotlib.pyplot as plt


def smooth_maximum(x, x1_func, x2_func, beta=0.0):
    """
    Smooth Maximum 
    :param x: The input variable
    :param x1_func: The functor of n1
    :param x2_func: The functor of n2
    :param beta: The beta value
    :return: 
    """
    a_x = x1_func(x)
    b_x = x2_func(x)

    e_beta_a_x = np.exp(beta * a_x)
    e_beta_b_x = np.exp(beta * b_x)

    return ((a_x * e_beta_a_x) + (b_x * e_beta_b_x)) / (e_beta_a_x + e_beta_b_x)

从ReLU推广到Swish¶

考虑平滑形式下的ReLU，即

代入公式我们得到

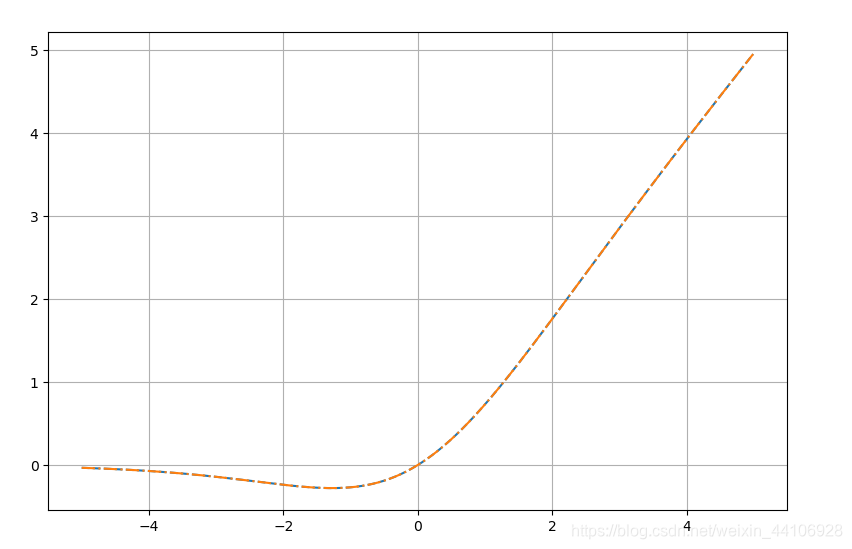
而这个结果就是Swish激活函数！所以我们可以得到，Swish激活函数是ReLU函数的一种平滑近似。我们称其为ACON-A

我们也可以用上述代码验证下

def swish(x, beta=1.0):
    return beta * x / (1 + np.exp(-x))


Acon_a = lambda x: smooth_maximum(x, x1_func=lambda x: x, x2_func=lambda x: 0, beta=1.0)

x = np.arange(-5, 5, 0.01).astype(np.float32)

acon_a_out = Acon_a(x)
swish_out = swish(x)

plt.plot(x, acon_a_out, ls='--')
plt.plot(x, swish_out, ls='-.')
plt.grid()
plt.show()

ACON-B¶

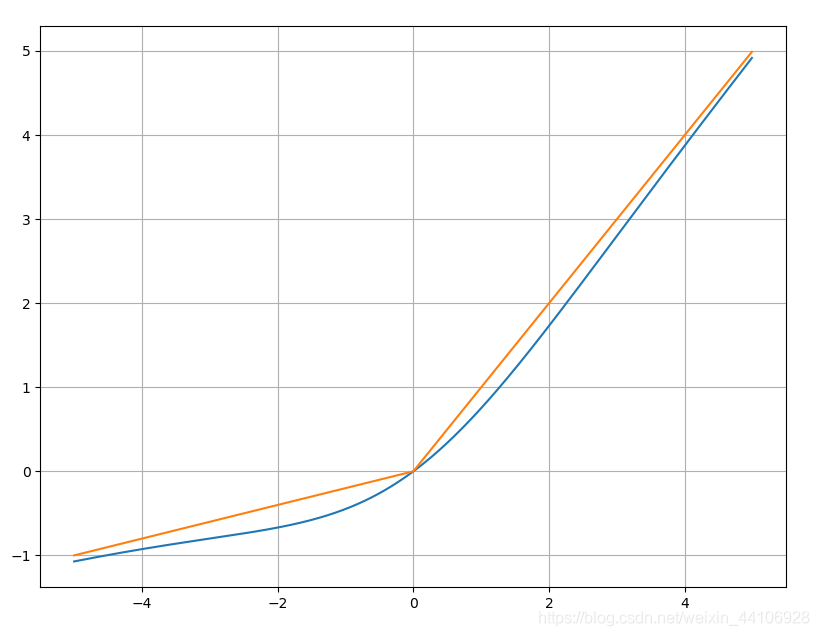
上述的平滑形式可以推广到ReLU激活函数家族里（PReLU，Leaky-ReLU) 因此我们提出了ACON-B的变体，即

我们按照前面的代码实验一下Leaky ReLU和它的平滑形式

def leaky_relu(x, beta):
    return np.maximum(x, beta * x)

Acon_b = lambda x: smooth_maximum(x, x1_func=lambda x: x, x2_func=lambda x: 0.2 * x, beta=1.0)

x = np.arange(-5, 5, 0.01).astype(np.float32)
acon_b_out = Acon_b(x)
leaky_relu_out = leaky_relu(x, 0.2)

plt.plot(x, acon_b_out)
plt.plot(x, leaky_relu_out)

plt.grid()
plt.show()

ACON-C¶

最后我们提出最广泛的一种形式ACON-C，即

它能涵盖之前的，甚至是更复杂的形式，在代码实现中，p1和p2使用的是两个可学习参数来自适应调整

我们简单看下ACON-C的函数性质

对其求一阶导，可以得到

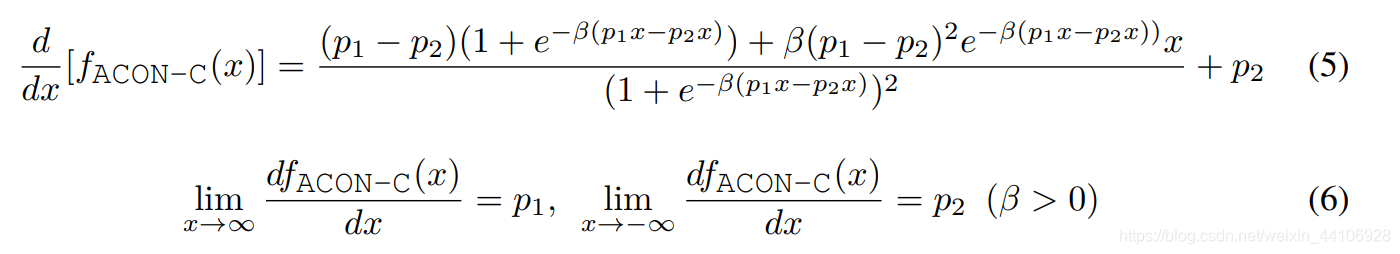
当 x 趋近于正无穷时，其梯度为 p1，当x趋近于负无穷时，其梯度为 p2。

对其求二阶导，有

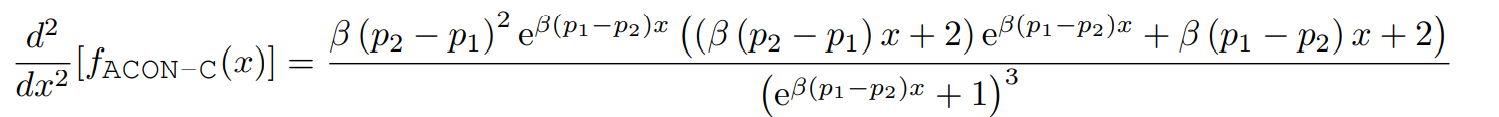
为了得到一阶导的上下界，我们令其二阶导为0，求得一阶导上下界分别为

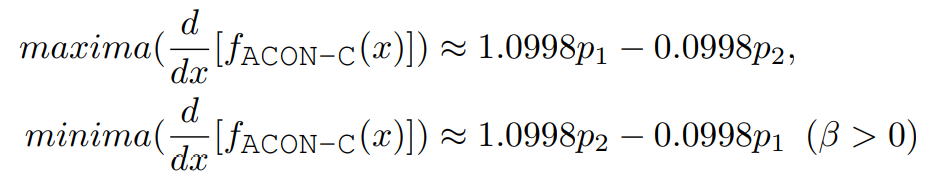
可以看到ACON-C下，一阶导的上下界也是通过p1和p2两个参数来共同决定的

最后总结下各个形态的公式

Meta-ACON¶

前面我们有提到，ACON系列的激活函数通过 $\beta$ 的值来控制是否激活神经元（$\beta$为0，即不激活）。因此我们需要为ACON设计一个计算 $\beta$ 的自适应函数。

而自适应函数的设计空间包含了layer-wise，channel-wise，pixel-wise这三种空间，分别对应的是层，通道，像素。

这里我们选择了channel-wise，首先分别对H, W维度求均值，然后通过两个卷积层，使得每一个通道所有像素共享一个权重。公式如下

为了节省参数量，我们在$W_1(C*C/r)$和$W_2(C/r*C)$之间加了个缩放参数r，我们设置为16

代码解读¶

具体的代码很简单，实现为：

import torch
from torch import nn

class MetaAconC(nn.Module):
    r""" ACON activation (activate or not).
    MetaAconC: (p1*x-p2*x) * sigmoid(beta*(p1*x-p2*x)) + p2*x
    """
    def __init__(self, width):
        super().__init__()
        self.fc1 = nn.Conv2d(width, width//16, kernel_size=1, stride=1, bias=False)
        self.fc2 = nn.Conv2d(width//16, width, kernel_size=1, stride=1, bias=False)

        self.p1 = nn.Parameter(torch.randn(1, width, 1, 1))
        self.p2 = nn.Parameter(torch.randn(1, width, 1, 1))

        self.sigmoid = nn.Sigmoid()

    def forward(self, x, **kwargs):
        beta = self.sigmoid(self.fc2(self.fc1(x.mean(dim=2, keepdims=True).mean(dim=3, keepdims=True))))
        return (self.p1 * x - self.p2 * x) * self.sigmoid( beta * (self.p1 * x - self.p2 * x)) + self.p2 * x

首先作者设置了p1和p2这两个可学习参数，并且设置了fc1和fc2两个1x1卷积。 在前向过程中，首先计算beta，x首先在H和W维度上求均值，然后经过两层1x1卷积，最后由sigmoid激活函数得到一个(0, 1)的值，用于控制是否激活。

接着就是按照前面的公式进行计算，大家可以参考上文的图

实验¶

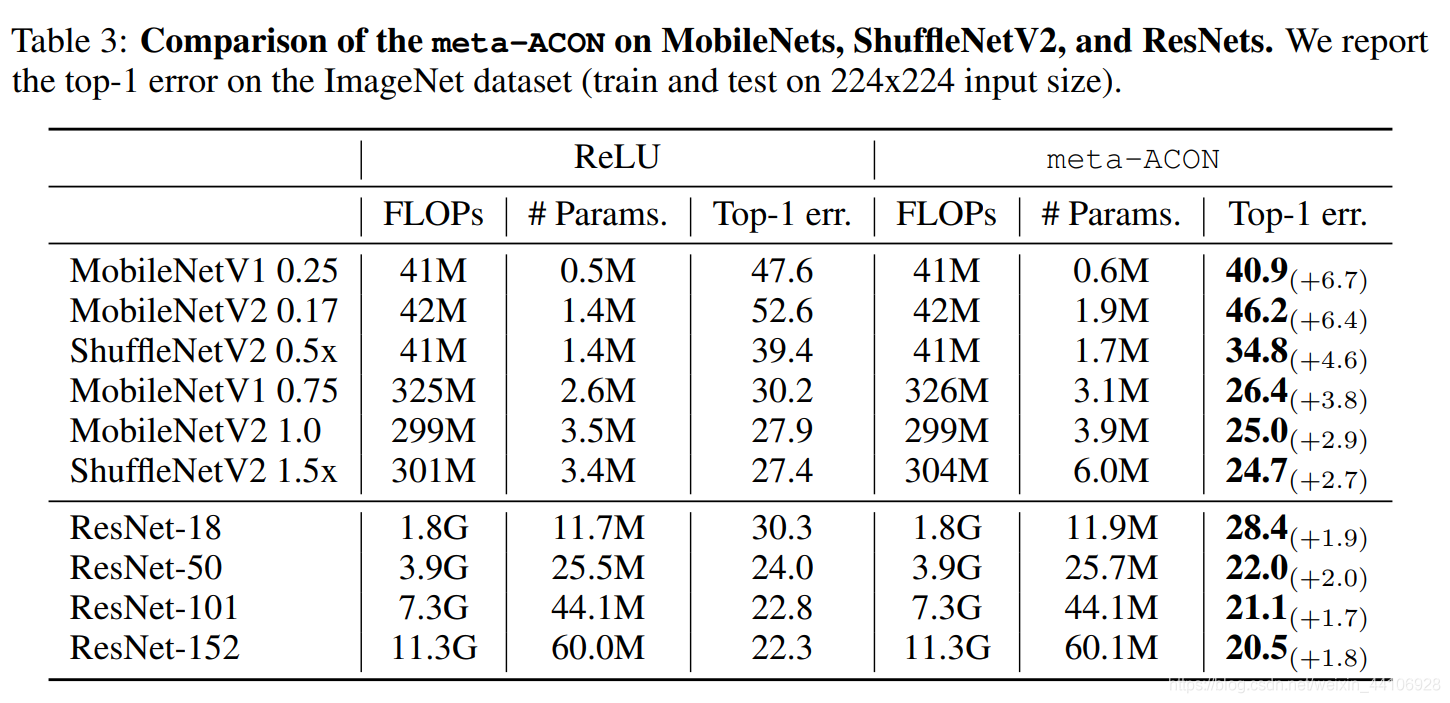
作者针对不同大小的网络做出了调整，针对小网络它替换了所有ReLU激活层，针对大网络（如ResNet50/101）只替换了每一个Block中3x3卷积后面的ReLU激活层，作者怎么设置的理由是避免过拟合，但我个人认为如果全都换成Meta-ACON，额外增加的参数量是很大的。

Meta-ACON虽然带来了一定的参数量，但是对大网络和小网络上都是有一定的提升

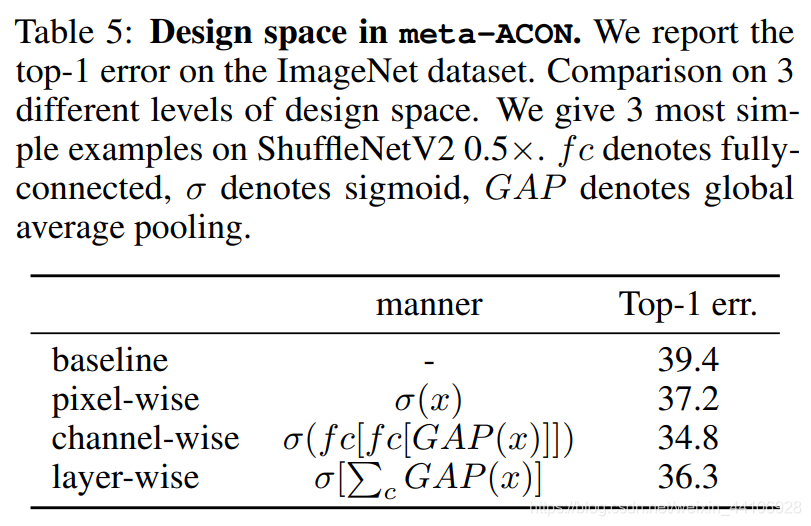
作者还针对设计空间做了一系列消融实验，其中channel-wise的效果是最好的

小结¶

该工作是之前旷视FReLU激活函数，ShuffleNet的作者MaNingNing提出的，构思十分巧妙，将ReLU和NAS搜索出来的Swish激活函数联系起来，并推广到一般的形式，为了让网络自适应的调整是否激活，设置了两层1x1卷积来控制。从实验上也从各个角度论证其有效性，期待后续对激活函数的进一步探索。

欢迎关注GiantPandaCV, 在这里你将看到独家的深度学习分享，坚持原创，每天分享我们学习到的新鲜知识。( • ̀ω•́ )✧

有对文章相关的问题，或者想要加入交流群，欢迎添加BBuf微信：

为了方便读者获取资料以及我们公众号的作者发布一些Github工程的更新，我们成立了一个QQ群，二维码如下，感兴趣可以加入。