基于 Discrete Diffusion 的模型不可知分割细化¶

目录¶

引言
相关工作
Forward diffusion process
Reverse diffusion process
推理过程
实验
总结
参考

引言¶

这次这篇文章介绍一篇很有意思的工作：SegRefiner，来自 NeurIPS, 2023，目前代码已开源。SegRefiner 的效果：请添加图片描述

SegRefiner 提出一种新的的任务解释，将分割细化视为一个数据生成过程。因此，细化可以通过一系列去噪扩散步骤来实现，其中 Coarse Mask 是 Ground Truth 的噪声版本。此外，为了处理二值掩模，进一步设计了一种新颖的离散扩散过程，在该过程中，每个像素执行单向随机状态转换。所提出的过程可以在训练期间逐渐将 Ground Truth 转换为 Coarse Mask，并在推理期间使用 Coarse Mask 作为采样起点。换句话说，SegRefiner 将掩模细化任务表述为一个条件生成问题，其中输入图像（指原图）作为条件，用于迭代更新/细化 Coarse Mask 中的错误预测。

SegRefiner 是模型不可知的，因此适用于不同的分割模型和任务。SegRefiner 验证的任务包括：语义分割，实例分割和二分图像分割。

Forward diffusion process¶

在介绍前向过程之前，先看一下整体框架的实现：

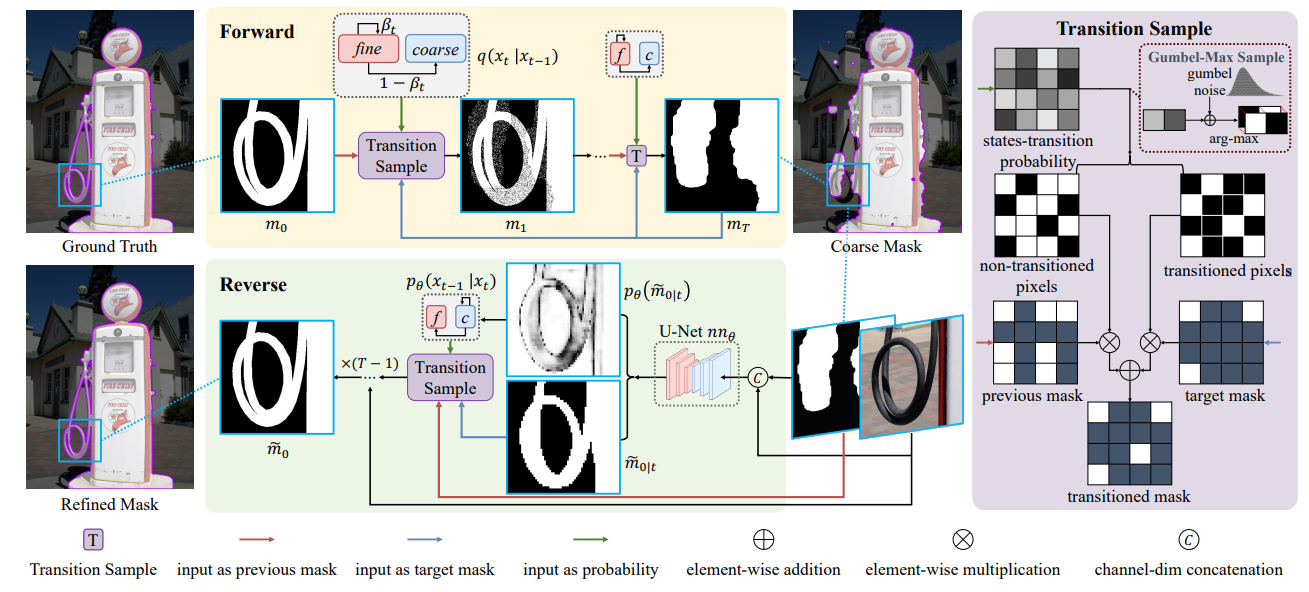
请添加图片描述

右侧是提出的 transition sample 模块，它基于输入状态转换概率从当前掩模中随机采样像素，并改变它们的值以匹配目标掩模中的值（也就是完成我们在引言中提到的“每个像素执行单向随机状态转换”）。看这张框架图的时候，注意区分不同 pipeline 的颜色区分，这里吐槽一下，我第一看 transition sample 没有清楚的看到三种输入。

在训练期间，转换样本模块将 Ground Truth 转换为 Coarse Mask，因此 Coarse Mask 是目标掩模。在推理过程中，目标掩模指的是预测的细致掩模，这个模块根据预测的细致掩模和转换概率在每个时间步中更新 Coarse Mask 中的值。

接下来仔细介绍下前向过程：

这种方法涉及将一个精细的 mask 逐渐转变为一个更粗糙的 mask，包含以下关键要素：

起始状态 (mo)：与 ground truth 的精细 mask 相对应。
目标状态 (mr)：一个粗糙的 mask。
中间状态 (mt)：随着时间步 t 的增加，逐渐从 mo 向 mr 演变的中间状态。

转移采样模块¶

引入了“转移采样”模块，该模块负责根据当前 mask mt、粗 mask mr 以及状态转移概率来进行状态的转移。状态的转移是单向的，保证了最终会收敛到粗糙 mask mr。

重参数技巧¶

此外，SegRefiner 还提到了重参数技巧（reparameterization trick），通过引入二元随机变量 x 来描述这一过程。该过程允许直接获取任何中间时间步的 mask mt，而无需逐步采样。具体表述为：

定义 x 表示为一个 one-hot 向量，表示中间掩模 mt 中像素 (i, j) 的状态。
设置 xi = [1, 0] 和 xi = [0, 1] 分别表示精细状态和粗糙状态。
因此，前向过程可以表示为公式：

$q\left(x_t^{i, j} \mid x_{t-1}^{i, j}\right)=x_{t-1}^{i, j} Q_t, \quad$ where $Q_t=\left[\begin{array}{cc}\beta_t & 1-\beta_t \\ 0 & 1\end{array}\right]$

$\beta_t \in[0,1]$ 为超参数，而 $1-\beta_t$ 对应了上述的状态转移概率。状态转移矩阵 $Q_t$ 的边缘分布可以表示为：

$q\left(x_t^{i, j} \mid x_0^{i, j}\right)=x_0^{i, j} Q_1 Q_2 \ldots Q_t=x_0 \bar{Q}_t=x_0\left[\begin{array}{cc}\bar{\beta}_t & 1-\bar{\beta}_t \\ 0 & 1\end{array}\right]$

整体上还是遵循 DDPM，但是引入二元随机变量 x 。

Reverse diffusion process¶

将粗糙 mask mr 逐渐修正为精细 mask mo。

由于此时精细 mask mo 和状态转移概率未知，对照着 SegRefiner 框架图来看，训练一个神经网络 $f_\theta$ 来预测精细 $\left.\operatorname{mask} \tilde{m}_0\right|_t$ ，表示为：

$\tilde{m}_{0 \mid t}, p_\theta\left(\tilde{m}_{0 \mid t}\right)=f_\theta\left(I, m_t, t\right)$

其中 I 是相应的图像。

$\left.\operatorname{mask} \tilde{m}_0\right|_t$ 和 $p_\theta\left(\tilde{m}_{0 \mid t}\right)$ 分别表示预测的精细 mask 和其置信度分数。相应的， $p_\theta\left(\tilde{m}_{0 \mid t}\right)$ 可视作 $\left.\operatorname{mask} \tilde{m}_0\right|_t$ 中每个像素处于“精细状态”的概率。

反向状态转移概率¶

根据前向过程的设定和贝叶斯定理，延续 DDPM 的方法，我们可以由前向过程的后验概率和预测的 $p_\theta\left(\tilde{m}_{0 \mid t}\right)$ 得到反向过程的概率分布，表示为：

$p_\theta\left(x_{t-1}^{i, j} \mid x_t^{i, j}\right)=x_t^{i, j} P_{\theta, t}^{i, j}, \quad$ where $P_{\theta, t}^{i, j}=\left[\begin{array}{cc}1 & 0 \\ \frac{p_\theta\left(\tilde{m}_{0, t}\right)^{i, j}\left(\bar{\beta}_{t-1}-\bar{\beta}_t\right)}{1-p_\theta\left(\tilde{m}_{0, t}\right)^{i, j} \bar{\beta}_t} & \frac{1-p_\theta\left(\tilde{m}_{0, t}\right)^{i, j} \bar{\beta}_{t-1}}{1-p_\theta\left(\tilde{m}_{0, t}\right)^{i, j} \bar{\beta}_t}\end{array}\right]$

其中 $P_{\theta, t}^{i, j}$ 为反向过程的状态转移概率。

迭代修正过程¶

给定粗糙 mask mr 以及相应的图像 I，首先将所有像素初始化为粗糙状态 xi = [1, 0]。通过不断迭代地状态转移，逐渐修正 m_T 中的预测值。一个可视化如下图：

请添加图片描述

推理过程¶

给定一个粗糙的掩模和其对应的图像，我们首先初始化所有像素为粗糙状态。我们在以下步骤之间迭代：

前向过程：以获取 $\left.\operatorname{mask} \tilde{m}_0\right|_t$ 和 $p_\theta\left(\tilde{m}_{0 \mid t}\right)$ 。
计算反向状态转移矩阵： $P_{\theta, t}^{i, j}$ 并得到 $x_{t-1}$ 。
计算精细化的掩模：基于 $x_{t-1}$ ， $m_t$ 和 $\left.\operatorname{mask} \tilde{m}_0\right|_t$ 计算精细化的掩模 $m_{t-1}$ 。

这个过程（1）-（3）迭代进行，直到获得精细的掩模。

实验¶

分别训练了 LR-SegRefiner 和 HR-SegRefiner，数据集和具体的 settings 在 https://github.com/402-Lab/SegRefiner?tab=readme-ov-file#training 。

定性对比其他方法，觉得对比 U-Net 和 ISNet 的效果的确很明显。

请添加图片描述

总结¶

SegRefiner 是首个基于扩散的图像分割细化方法，采用了离散扩散过程。SegRefiner 执行模型不可知的分割细化，并在各种分割任务的细化中取得了强有力的实证结果。虽然它在准确度上取得了显著的提升，但其局限性在于扩散过程由于多步迭代策略而导致推理速度变慢。

参考¶

本文总阅读量次

基于 Discrete Diffusion 的模型不可知分割细化¶

目录¶

引言¶

相关工作¶

Forward diffusion process¶

转移采样模块¶

重参数技巧¶

Reverse diffusion process¶

反向状态转移概率¶

迭代修正过程¶

推理过程¶

实验¶

总结¶

参考¶