跳转至

ICLR 2023：基于 diffusion adversarial representation learning 的血管分割

目录

  • 前言
  • 概述
  • DDPM
  • switchable SPADE layer
  • 训练和推理
  • 定量结果和可视化
  • 总结
  • 参考链接

前言

目前对于血管分割任务，有两个问题：第一是数据量；第二是血管图像背景复杂。传统的监督方法需要大量的标签，无监督方法则因为血管图像一般背景复杂、低对比度、运动伪影和有许多微小的分支，分割结果达不到期望的准确率。对此，这篇论文引入了一种名为扩散对抗表示学习（DARL）的新架构。

自监督的学习的“标注”通常来自于数据本身，其常规操作是通过玩各种各样的“auxiliary task”来提高学习表征（representation）的质量，从而提高下游任务的质量。对于自监督的血管分割任务，DARL 使用 diffusion module 学习背景信号，利于生成模块有效地提供血管表达信息。此外，该模型使用基于可切换的空间自适应去规范化 (spatially adaptive denormalization, SPADE) 的对抗学习来合成假的血管图像和血管分割图，用来捕获与血管相关的语义信息。训练完成后，该模型可以在单步中生成分割图，细节在后文介绍。

在阅读本篇文章之前有一些前置的概念需要掌握，可以参考：

  1. DP 大佬的一文弄懂 diffusion model，https://mp.weixin.qq.com/s/G50p0SDQLSghTnMAOK6BMA 。
  2. 表示学习（representation learning），https://zhuanlan.zhihu.com/p/112849395 。
  3. GANs，https://zhuanlan.zhihu.com/p/27386749 。

概述

首先，在自然图像上设计的无监督方法很难应用于医用血管图像。目前的一些自监督方法，需要两个不同的对抗网络来分割血管，带来了训练的复杂性。因此，需要一种新的分割方法，该方法可以在无监督的情况下有效地对血管进行分割，并且无需大量的带标记数据。DARL 模型将 DDPM 和对抗学习应用于血管分割。即使用 diffusion module 学习背景信号，进行自监督的血管分割，这使生成模块能够有效地提供血管表达信息。此外，该模型基于可切换的 SPADE，通过对抗学习来合成假血管图像和血管分割图，进一步使该模型捕获了与血管相关的语义信息。

DDPM 已成功应用于许多低级计算机视觉任务，例如超分辨率、修复和着色。但是，它在高级视觉任务（例如没有标签数据的语义分割）中的应用很少，工作原理是学习从高斯噪声到数据的反向扩散过程的马尔可夫变换，这个在 DP 大佬的文章中有一些相关介绍。扩散模型的采样过程通常需要相对较长的时间，这意味着使用 DDPM 生成新图像可能很耗时。

如下图所示，DARL 模型由扩散模块和生成模块组成，生成模块通过对抗学习来学习血管的语义信息。扩散模块估计添加到受干扰的输入数据中的噪声，对抗学习模型为扩散模块输出的噪声向量生成图像。扩散模型与对抗模型相连，使该模型能够实时生成图像，并对血管进行分割。

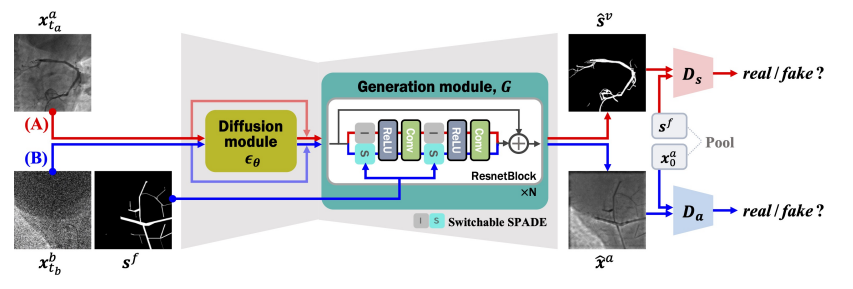
在这里插入图片描述

生成模块中使用了空间自适应去规范化 (SPADE) 层的可切换版本来同时估计血管分割图和基于掩膜的假血管造影。该模型输入未配对的背景图像和血管造影图像，这些图像是在注射造影剂之前和之后拍摄的。向拟议模型提供输入的途径有两种：（A）当给出真实的血管造影图像时，使用没有 SPADE 的模型估计血管分割图；（B）当给出背景图像时，带有 SPADE 的模型会生成合成血管造影，将类似血管的掩码（伪掩码）与输入背景混合在一起。（B）路径中的每个伪掩码都可以视为生成的血管造影图像的伪标签。通过将合成血管造影再次输入（A）路径，即应用分割图和伪掩码标签之间的周期一致性来捕获血管的语义信息。

我们简单梳理一下这里的逻辑。首先输入是原图（没有标签），背景图像（来源于数据集）和随机的伪掩码（来源于数据集）三个，原图输入（A）路径，背景图像输入（B）路径，伪掩码输入生成模块的 SPADE，SPADE 会判断有没有伪掩码从而做不同的标准化动作。两条路径分别产生两种不同的输出，分别为原图的预测结果和合成的假血管造影图。上图的右侧，有两个判别器，分别为：原图的预测结果和伪掩码对抗；合成的假血管造影图和原图对抗。最后，生成的假血管造影图和伪掩码可以用来再次迭代训练该网络，整个是一个自监督的过程。总之，在 GANs 的框架基础上，以自监督的方式，加入了 diffusion module。

DDPM

前向扩散的过程，可以理解为一个马尔可夫链，即通过逐步对一张真实图片添加高斯噪声直到最终变成纯高斯噪声图片：

q\left(\boldsymbol{x}_t \mid \boldsymbol{x}_{t-1}\right)=\mathcal{N}\left(\boldsymbol{x}_t ; \sqrt{1-\beta_t} \boldsymbol{x}_{t-1}, \beta_t \boldsymbol{I}\right)

其中，βt 是指固定方差(0~1)。在采样得到 xt 的时候并不是直接通过高斯分布 q(xt|xt-1) 采样，而是用了一个重参数化的技巧。

前向扩散过程还有个属性，可以直接从 x0 采样得到中间任意一个时间步的噪声图片 xt，所以可以写成：

q\left(x_t \mid x_0\right)=\mathcal{N}\left(x_t ; \sqrt{\alpha_t} x_0,\left(1-\alpha_t\right) I\right)

其中，

\alpha_t=\Pi_{s=1}^t\left(1-\beta_s\right)

逆过程如下：

p_\theta\left(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_t\right)=\mathcal{N}\left(\boldsymbol{x}_{t-1} ; \boldsymbol{\mu}_\theta\left(\boldsymbol{x}_t, t\right), \sigma_t^2 \boldsymbol{I}\right)

上面的公式中，方差是固定的，均值是噪声向量 ϵθ 的，是可以训练的参数。

\boldsymbol{\mu}_\theta\left(\boldsymbol{x}_t, t\right)=\frac{1}{\sqrt{1-\beta_t}}\left(\boldsymbol{x}_t-\frac{\beta_t}{\sqrt{1-\alpha_t}} \boldsymbol{\epsilon}_\theta\left(\boldsymbol{x}_t, t\right)\right)

最后，采样过程通过迭代可以生成任意一个时间步的噪声图片，z 是标准的高斯分布：

\boldsymbol{x}_{t-1}=\boldsymbol{\mu}_\theta\left(\boldsymbol{x}_t, t\right)+\sigma_t \boldsymbol{z}

关于 DDPM 的其他内容，这里就不详细展开了。

switchable SPADE

归一化有助于减少混乱的背景结构对血管分割的影响，而空间自适应和可切换的参数使模型能够适应不同的图像区域和血管图像大小。为了方便，这一部分以图片的方式总结如下: 在这里插入图片描述

训练和推理

论文中给出的训练和推理流程图，看起来有点乱，在下图中，我把每一个输入和中间变量都标记出来了。

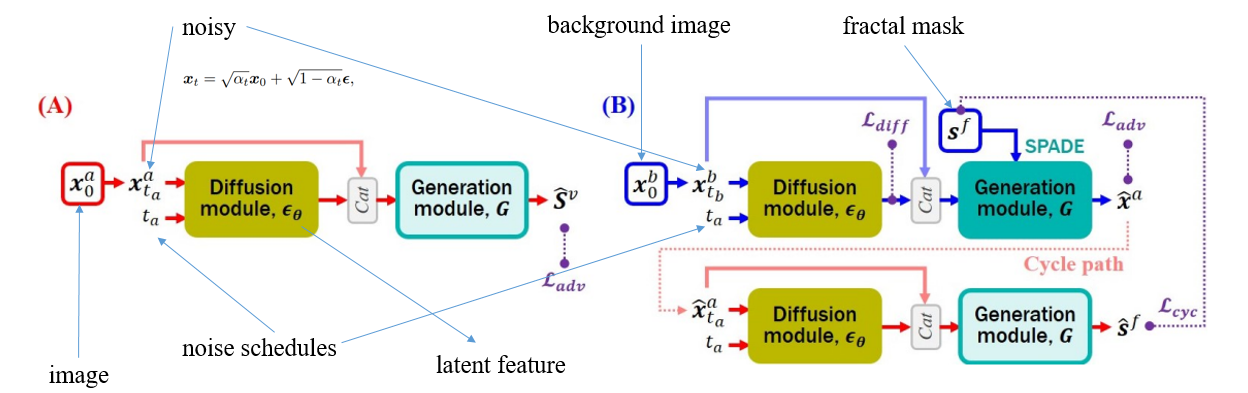
在这里插入图片描述

可以看到，在（B）路径中存在 Cycle path，即把通过扩散模块和对抗网络生成的假图像和伪掩码，再次输入（A）路径训练，完成自监督的过程。

关于里面涉及到的损失函数，整理如下：

\min _{\boldsymbol{\theta}, G} \mathcal{L}^G\left(\boldsymbol{\epsilon}_{\boldsymbol{\theta}}, G, D_s, D_a\right), \quad \min _{D_s, D_a} \mathcal{L}^D\left(\boldsymbol{\epsilon}_{\boldsymbol{\theta}}, G, D_s, D_a\right),

这两个分别表示 diffusion/生成器和判别器的损失函数:

\begin{aligned} & \mathcal{L}^G\left(\boldsymbol{\epsilon}_{\boldsymbol{\theta}}, G, D_s, D_a\right)=\mathcal{L}_{d i f f}\left(\boldsymbol{\epsilon}_{\boldsymbol{\theta}}\right)+\alpha \mathcal{L}_{a d v}^G\left(\boldsymbol{\epsilon}_{\boldsymbol{\theta}}, G, D_s, D_a\right)+\beta \mathcal{L}_{c y c}\left(\boldsymbol{\epsilon}_{\boldsymbol{\theta}}, G\right), \\ & \mathcal{L}^D\left(\boldsymbol{\epsilon}_{\boldsymbol{\theta}}, G, D_s, D_a\right)=\mathcal{L}_{a d v}^{D_s}\left(\boldsymbol{\epsilon}_{\boldsymbol{\theta}}, G, D_s\right)+\mathcal{L}_{a d v}^{D_a}\left(\boldsymbol{\epsilon}_{\boldsymbol{\theta}}, G, D_a\right), \end{aligned}

其中的三个小 loss，Diffusion loss:

\mathcal{L}_{\text {diff }}\left(\boldsymbol{\epsilon}_{\boldsymbol{\theta}}\right):=\mathbb{E}_{t, \boldsymbol{x}_0, \boldsymbol{\epsilon}}\left[\left\|\boldsymbol{\epsilon}-\boldsymbol{\epsilon}_\theta\left(\sqrt{\alpha_t} \boldsymbol{x}_0+\sqrt{1-\alpha_t} \boldsymbol{\epsilon}, t\right)\right\|^2\right] .

Adversarial loss: 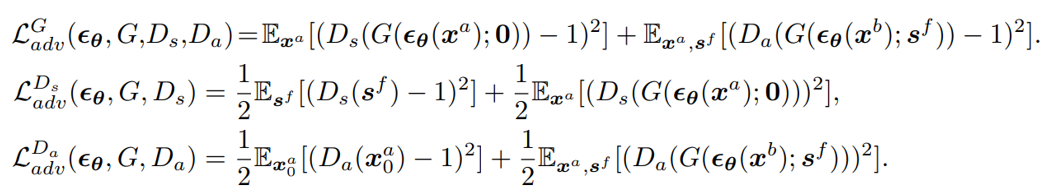在这里插入图片描述 Cyclic reconstruction loss 很简单，在图中就可以看出来，可以理解为是伪掩码和网络利用合成的血管图预测出的掩码之间的 MSE。

模型在推理过程中不需要迭代反向过程，这与传统的扩散模型不同。意味着，一旦训练了 DARL 模型，就可以从 (A) 路径中单步获得血管分割掩码。

定量结果和可视化

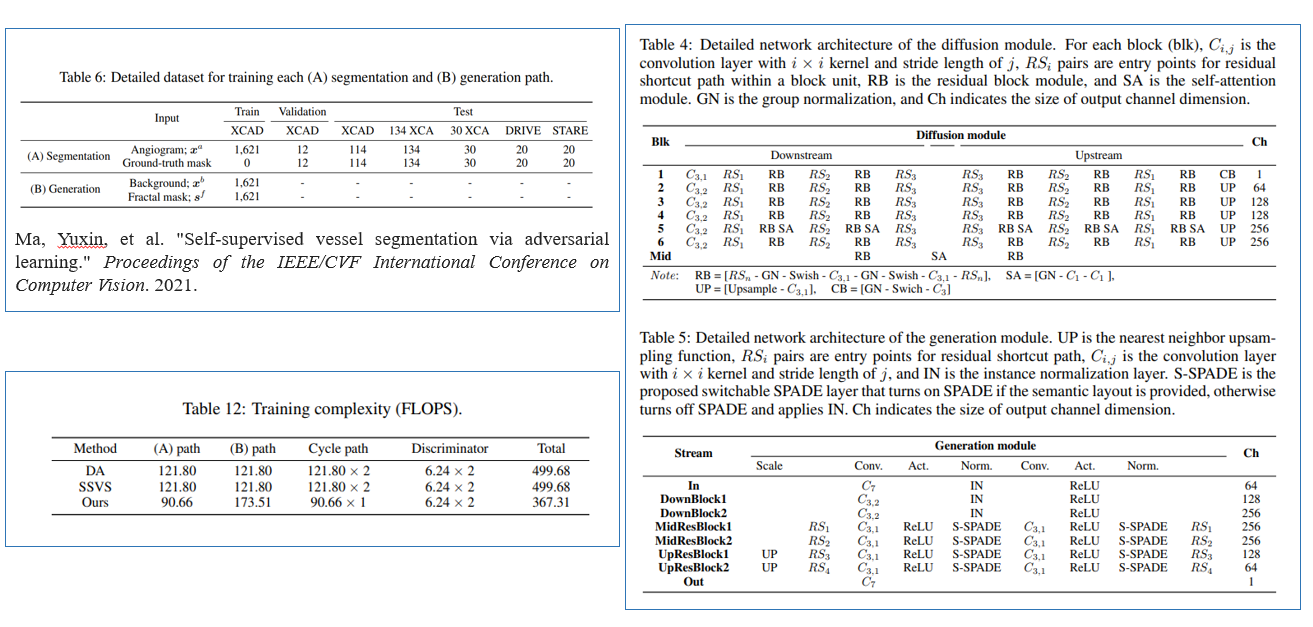
数据集、模型实现细节和模型复杂度如下图： 在这里插入图片描述

可视化结果和定量结果如下图：

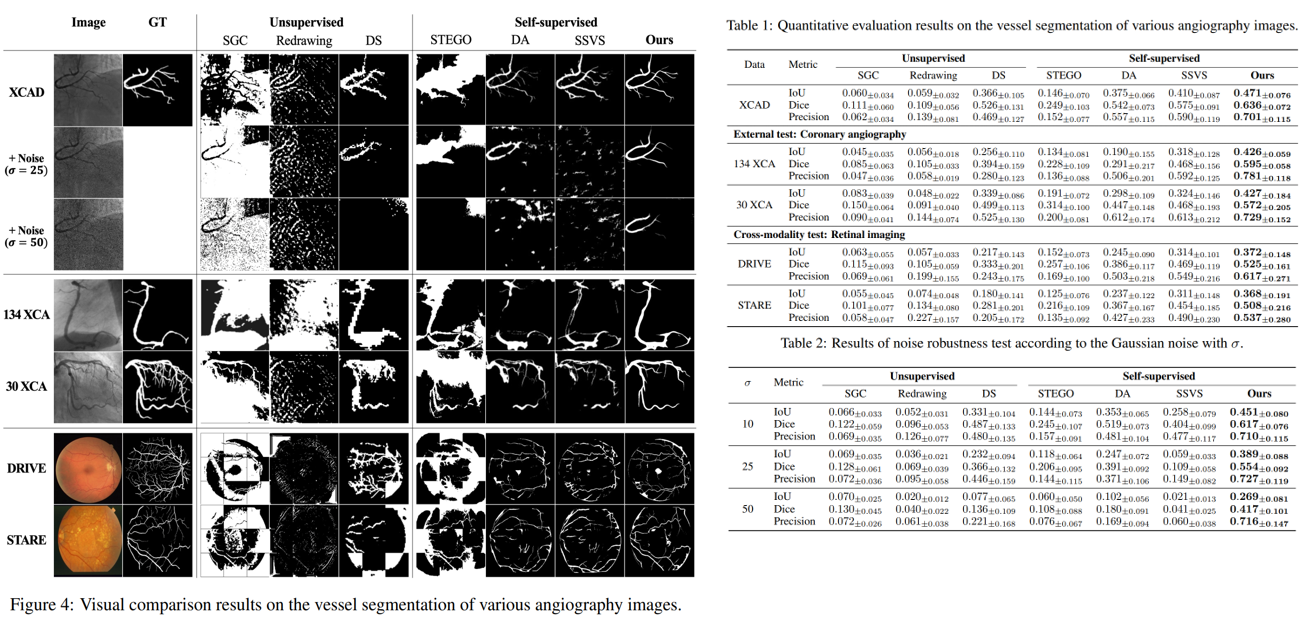
在这里插入图片描述

该模型之所以能够在噪声条件下表现良好，是因为它是通过扰乱输入图像的 diffusion module 训练的，因此即使从噪声数据中也可以非常坚固地分割血管结构。

消融实验部分如下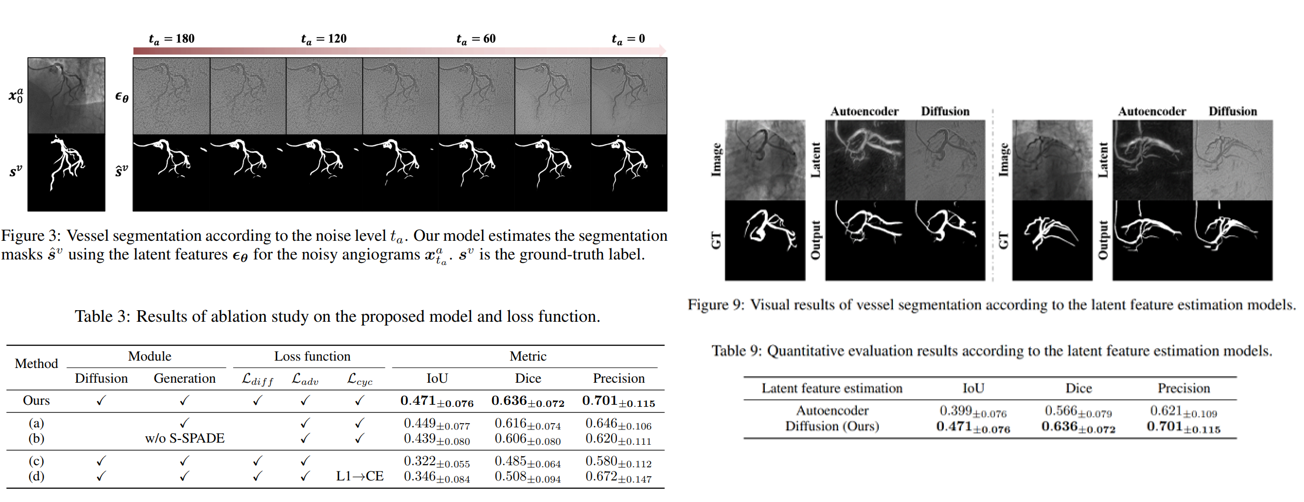： 在这里插入图片描述 左上角是不同时间步的高斯噪声，模型经过（A）路径预测出的分割图，从左往右效果是越来越好的，这个地方还是很好理解的，DPM 中也是反向迭代次数直到扩散的周期效果才最好。

总结

这篇文章提出 DARL 的扩散模型，用于自监督的血管分割任务。该模型利用扩散模块和生成模块，在不使用标签的情况下学习血管的表示，并通过可切换 SPADE 层生成合成血管造影图像和血管分割掩膜，更有效地学习血管的语义信息。尽管扩散模块的训练结合了其他损失函数，但推断不是迭代的，只在一步中完成，这使得该模型比现有的扩散模型更快速和独特。也使用各种医学血管数据集验证了该模型的优越性，并指出该模型具有鲁棒性。

这篇阅读笔记 PPT 版本的 Github 地址：https://github.com/lixiang007666/diggersPPT/blob/main/DARL.pdf

关于 Diffusion Models 在医学图像分割上的应用还有一些，后面还会介绍的~

参考链接

本文总阅读量次