跳转至

Pytorch中的四种经典Loss源码解析

【GiantPandaCV导语】笔者最近在OneFlow框架对齐实现Pytorch相关Loss代码，其中也涉及到部分源码解读，数学特殊操作等知识，于是想写篇文章简单总结一下。

关于Pytorch的Loss源码

了解过Pytorch的应该知道其历史包袱比较重，它吸收了Caffe2的底层代码，然后自己借用这部分底层代码来写各种OP的逻辑，最后再暴露出一层Python接口供用户使用。

因此第一次接触Pytorch源代码可能有点不太熟悉，基本上Pytorch大部分OP逻辑实现代码都放在 Aten/native下，我们这里主要是根据Loss.cpp来进行讲解

MarginRankingLoss

RankingLoss系列是来计算输入样本的距离，而不像MSELoss这种直接进行回归。 其主要思想就是分为 Margin 和 Ranking。

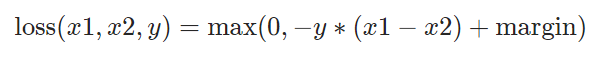
MarginRankingLoss公式

Margin 这个词是页边空白的意思，平常我们打印的时候，文本内容外面的空白就叫 Margin。

而在Loss中也是表达类似的意思，相当于是一个固定的范围，当样本距离（即Loss）超过范围，即表示样本差异性足够了，不需要再计算Loss。

Ranking 则是排序，当target=1，则说明x1排名需要大于x2；当target=2，则说明x2排名需要大于x1。

其源码逻辑也很简单，就是根据公式进行计算，最后根据reduction类型来进行 reduce_mean/sum Pytorch的MarginRankingLoss代码 下面是对应的numpy实现代码

def np_margin_ranking_loss(input1, input2, target, margin, reduction):
    output = np.maximum(0, -target*(input1 - input2) + margin)
    if reduction == "mean":
        return np.mean(output)
    elif reduction == "sum":
        return np.sum(output)
    else:
        return output

TripletMarginLoss

TripletLoss最早是在 FaceNet 提出的，它是用于衡量不同人脸特征之间的距离，进而实现人脸识别和聚类

TripletLoss

而TripletMarginLoss则是结合了TripletLoss和MarginRankingLoss的思想，具体可参考 Learning local feature descriptors with triplets and shallow convolutional neural networks

其公式如下

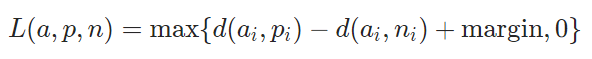
TripletMarginLoss公式

其中d是p范数函数

距离函数

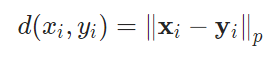
范数的具体公式是

范数公式

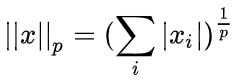
该Loss针对不同样本配对，有以下三种情况

  1. 简单样本，即
d(ai, pi) + margin < d(ai, ni)

此时 正样本距离anchor的距离d(ai, pi) + Margin仍然小于负样本距离anchor的距离d(ai, ni)，该情况认为正样本距离足够小，不需要进行优化，因此Loss为0

  1. 难样本，即
d(ai, ni) < d(ai, pi)

此时 负样本距离anchor的距离d(ai, ni) 小于 正样本距离anchor的距离d(ai, pi)，需要优化

  1. 半难样本，即
d(ai, pi) < d(ai, ni) < d(ai, pi) + margin

此时虽然 负样本距离anchor的距离d(ai, ni) 大于 正样本距离anchor的距离d(ai, pi)，但是还不够大，没有超过 Margin，需要优化

source: https://omoindrot.github.io/triplet-loss

此外论文作者还提出了 swap 这个概念，原因是我们公式里只考虑了anchor距离正类和负类的距离，而没有考虑正类和负类之间的距离，考虑以下情况

Swap

可能Anchor距离正样本和负样本的距离相同，但是负样本和正样本的距离很近，不利于模型区分，因此会做一个swap，即交换操作，在代码里体现的操作是取最小值。

## 伪代码
if swap: 
    D(a, n) = min(D(a,n), D(p, n))

这样取了最小值后，在Loss计算公式中，Loss值会增大，进一步帮助区分负样本。

有了前面的铺垫，我们理解Pytorch的TripletMarginRankingLoss源码也非常简单

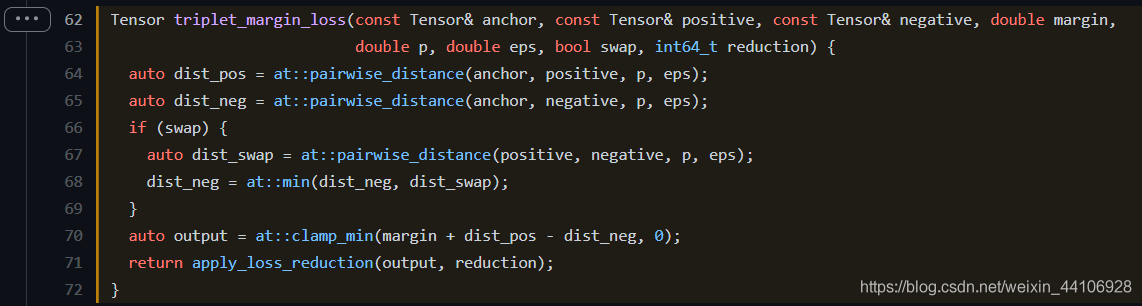
TripletMarginLoss源码

at::pairwise_distance是距离计算函数，首先计算出了anchor与正类和负类的距离。 然后根据参数swap，来确定是否考虑正类和负类之间的距离。 最后output就是按照公式进行计算，下面是numpy的对应代码

def np_triplet_margin_loss(anchor, postive, negative, margin, swap, reduction="mean", p=2, eps=1e-6):
    def _np_distance(input1, input2, p, eps):
        # Compute the distance (p-norm)
        np_pnorm = np.power(np.abs((input1 - input2 + eps)), p)
        np_pnorm = np.power(np.sum(np_pnorm, axis=-1), 1.0 / p)
        return np_pnorm

    dist_pos = _np_distance(anchor, postive, p, eps)
    dist_neg = _np_distance(anchor, negative, p, eps)

    if swap:
        dist_swap = _np_distance(postive, negative, p, eps)
        dist_neg = np.minimum(dist_neg, dist_swap)
    output = np.maximum(margin + dist_pos - dist_neg, 0)

    if reduction == "mean":
        return np.mean(output)
    elif reduction == "sum":
        return np.sum(output)
    else:
        return output

这里比较容易踩坑的是p范数的计算，因为当p=2，根据范数的公式，如果输入有负数是不合法的， 比如

\sqrt{-20} = ?

于是我们从distance函数开始找线索，发现它是调用at::norm pairwise_distance 根据Pytorch的文档，它其实在计算的时候调用了abs绝对值，来避免最后负数出现，从而保证运算的合理性Norm文档

KLDivLoss

该损失函数是计算KL散度（即相对熵），它可以用于衡量两个分布的差异

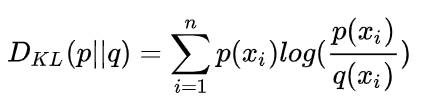
KL散度基本定义

当p和q分布越接近，则\frac{p(x)}{q(x)}趋近于1，经过log运算后，loss值为0

当分布差异比较大，则损失值就比较高

Pytorch中计算公式中还不太一样

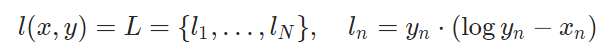
Pytorch的KLDivLoss公式

下面我们看看Pytorch对应的源码

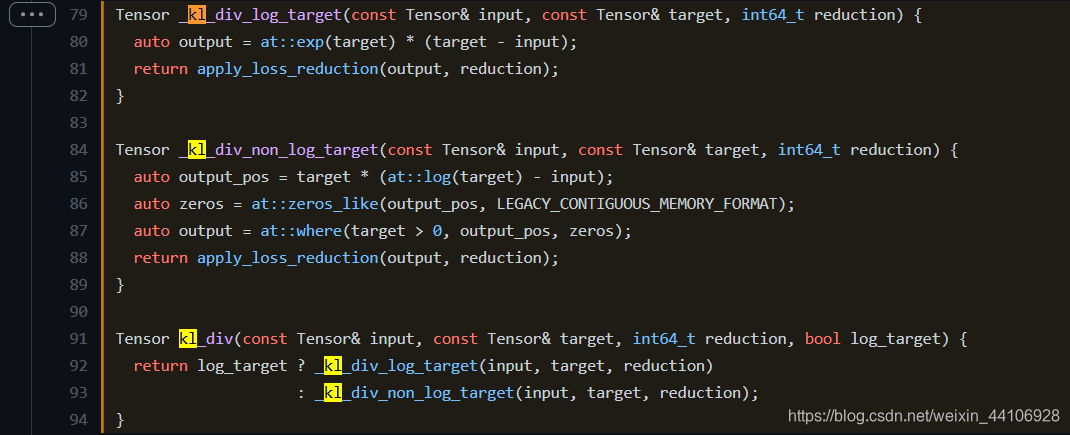
KLDivLoss源码

首先可以观察到，除了常规的input，target，reduction，还有一个额外的参数 log_target，用于表示target是否已经经过log运算。 根 据这个参数，KLDivLoss进而分成两个函数 _kl_div_log_target 和 _kl_div_non_log_target 实现。

_kl_div_log_target 的实现比较简单，就是按照公式进行计算

而 _kl_div_non_log_target 有些许不同，因为target的数值范围不确定，当为负数的时候，log运算时不合法的。因此Pytorch初始化了一个全0数组，然后在最后的loss计算中，在target小于0的地方填0，避免nan数值出现

下面是对应的numpy实现代码

def np_kldivloss(input, target, log_target, reduction="mean"):
    if log_target:
        output = np.exp(target)*(target - input)
    else:
        output_pos = target*(np.log(target) - input)
        zeros = np.zeros_like(input)
        output = np.where(target>0, output_pos, zeros)
    if reduction == "mean":
        return np.mean(output)
    elif reduction == "sum":
        return np.sum(output)
    else:
        return output

BCEWithLogitsLoss

熟悉二分类交叉熵损失函数BCELoss的应该知道，该函数输入的是个分类概率，范围在0~1之间，最后计算交叉熵。我们先看下该损失函数的参数 BCEWithLogitsLoss参数

  • weight 表示最后loss缩放权重
  • reduction 表示 最后是做mean, sum, none 操作
  • pos_weight 表示针对正样本的权重，即positive weight

下面是其计算公式 其中 \sigma 表示sigmoid运算

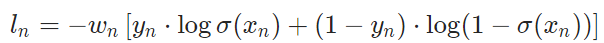
BCEWithLogitsLoss

BCEWithLogitsLoss 相当于 sigmoid + BCELoss，但实际上 Pytorch为了更好的数值稳定性，并不是这么做的，下面我们看看对应的源代码

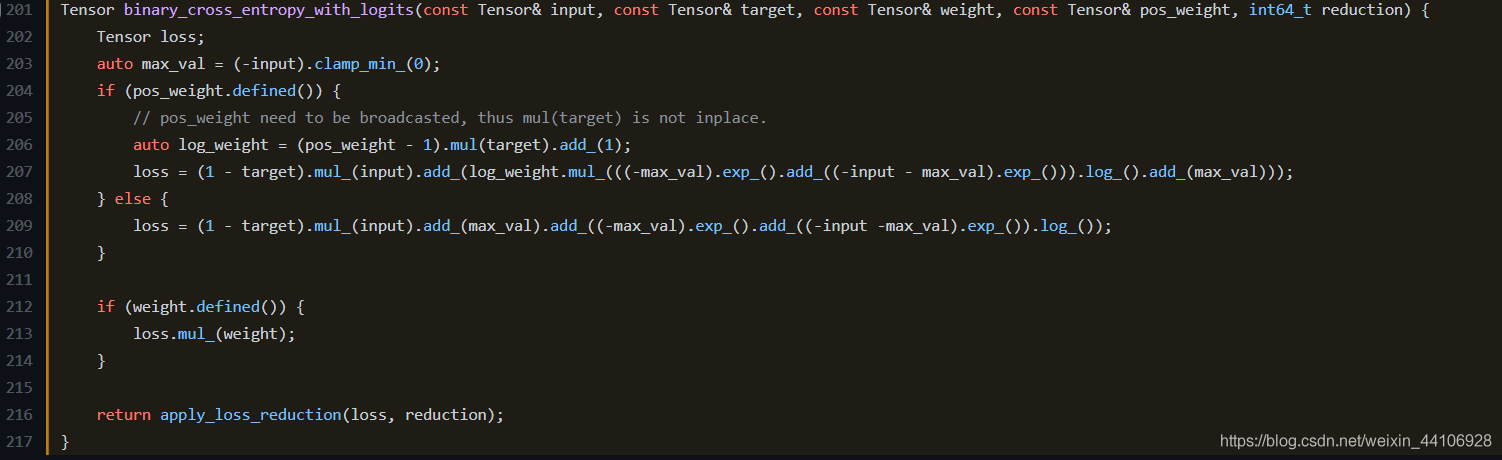
Pytorch的BCEWithLogitsLoss源码

这段源代码其实看的不太直观，我们可以看下numpy对应的代码

def np_bce_with_logits_loss(np_input, np_target, np_weight, np_pos_weight, reduction="mean"):
    max_val = np.maximum(-np_input, 0)

    if np_pos_weight.any():
        log_weight = ((np_pos_weight - 1) * np_target) + 1
        loss = (1 - np_target) * np_input
        loss_1 = np.log(np.exp(-max_val) + np.exp(-np_input - max_val)) + max_val
        loss += log_weight * loss_1
    else:
        loss = (1 - np_target) * np_input
        loss += max_val
        loss += np.log(np.exp(-max_val) + np.exp(-np_input - max_val))

    output = loss * np_weight

    if reduction == "mean":
        return np.mean(output)
    elif reduction == "sum":
        return np.sum(output)
    else:
        return output

因为涉及到了sigmoid运算，所以有以下公式

log(\sigma(x)) = log(\frac{1}{1+e^{-x}})
log(1-\sigma(x)) = log(\frac{e^{-x}}{1+e^{-x}})

计算中，如果x过大或过小，会导致指数运算e^x出现上溢或下溢，因此我们可以 用 log-sum-exp 的技巧来避免数值溢出，具体可以看下面公式推导（特此感谢德澎！）

公式推导

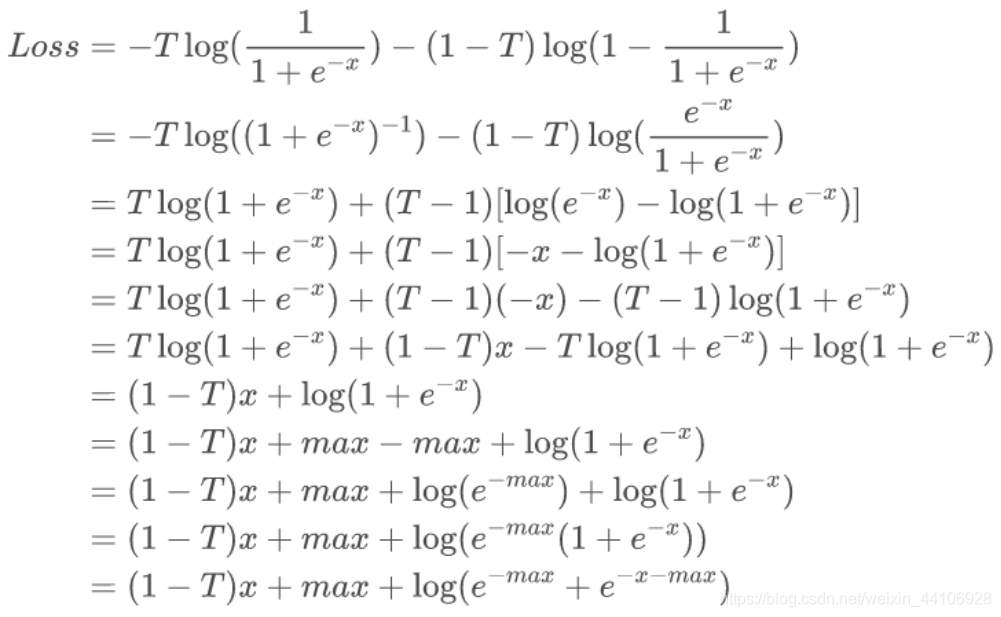
总结

看源代码没有想象中那么难，只要破除迷信，敢于尝试，你也能揭开源码的神秘面纱~

相关链接

  1. triplet-loss
  2. FaceNet
  3. TripletMarginLoss
  4. RankingLoss
本文总阅读量次