最新SOTA！隐式学习场景几何信息进行全局定位¶

1. 论文浅谈¶

全局视觉定位是指利用单张图像，根据已有的地图，估计相机的绝对姿态（位置和方向）。这种技术可以应用于机器人和增强/虚拟现实等领域。这篇文章的主要贡献是提出了一种利用姿态标签来学习场景的三维几何信息，并利用几何信息来估计相机姿态的方法。具体来说，作者设计了一个学习模型，它可以从图像中预测两种三维几何表示（X, Y, Z坐标），一种是相机坐标系下的，另一种是全局坐标系下的。然后，通过将这两种表示进行刚性对齐，就可以得到与姿态标签匹配的姿态估计。这种方法还可以引入额外的学习约束，比如最小化两种三维表示之间的对齐误差，以及全局三维表示和图像像素之间的重投影误差，从而提高定位精度。在推理阶段，模型可以实时地从单张图像中估计出场景的三维几何信息，并通过对齐得到姿态。作者在三个常用的视觉定位数据集上进行了实验，进行了消融分析，并证明了他们的方法在所有数据集上都超过了现有的回归方法的姿态精度，并且可以实时地从单张图像中估计出场景的三维几何信息，并通过对齐得到姿态。

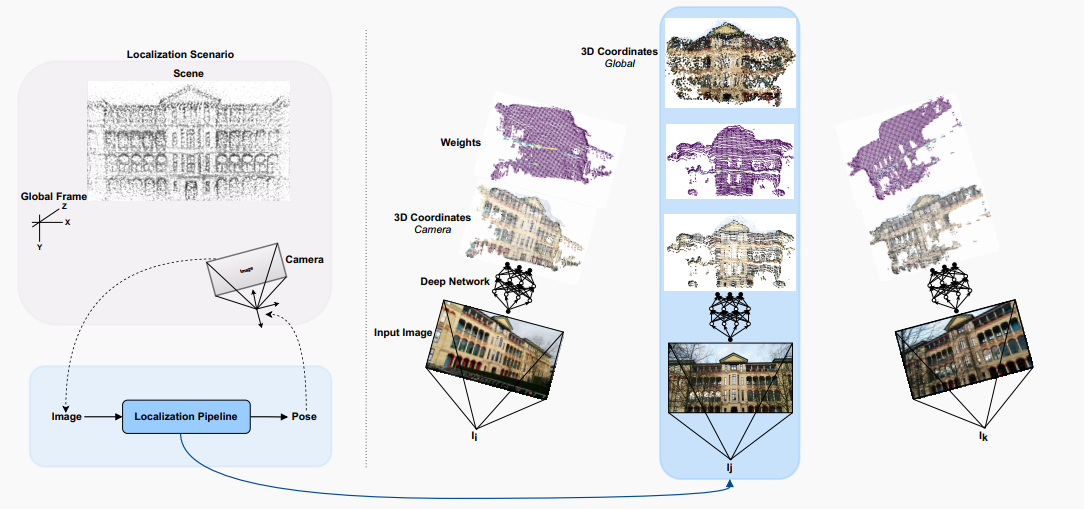
图1：我们在剑桥地标数据集(医院场景)的样本上的视觉定位方案的示意图。我们的方法只需要一组图像及其对应的姿态作为训练的标签。左侧：给定单个图像，我们的方法估计相机在给定场景中的全局姿态。右侧：我们展示了我们方案的中间输出，这些输出用于估计姿态。对于输入图像，所提出的过程估计两个点云和一组权重。第一个点云表示相机坐标系中的场景几何(X，Y，Z 坐标)，而第二个点云表示全局坐标系中的场景几何。这两个点云及预测的权重用于估计相机的全局姿态。在图 1 的右侧，我们可视化了三个样本输入图像，它们相应的间接估计的 $3D$ 场景表示(点云)和权重。在右上方，我们可以看到只有一个 $3D$ 点云，它对应于三个重叠的点云在全局坐标系中，也是由我们的算法估计的。尽管我们的方法隐式地估计场景在局部和全局参考系中的 $3D$ 点云表示，但它不是一个建图或 $3D$ 重建算法，而是一个定位算法，隐式地学习和使用 $3D$ 场景几何。

2. 原文摘要¶

全局视觉定位是在先前建模的区域中，从单个图像估计相机的绝对姿态。从单个图像获得姿态对于许多机器人和增强/虚拟现实应用具有重要意义。近年来，深度学习在计算机视觉领域取得了显著的进展，促进了许多方法的发展，这些方法直接从输入图像中回归出 $6$ 自由度姿态。然而，这些方法忽略了基础场景几何对于姿态回归的重要作用。单目重定位面临的一个主要困难是，可用于监督训练的数据非常稀少，只有图像对应的 $6$ 自由度姿态。为了解决这个问题，我们提出了一种新颖的方法，它能够利用这些极少的可用标签(即姿态)来学习场景的 $3D$ 几何，并利用几何信息来估计相机的 $6$ 自由度姿态。我们提出了一种基于学习的方法，它利用这些姿态标签和刚性配准来学习两个 $3D$ 场景几何表示，分别是相机坐标系下的(X，Y，Z)坐标和全局坐标系下的(X，Y，Z)坐标。给定单个图像，我们的方法可以估计出这两个 $3D$ 场景表示，然后通过将它们配准来估计出与姿态标签一致的姿态。这种表达方式使我们能够引入额外的学习约束，以最小化两个 $3D$ 场景表示之间的 $3D$ 配准误差和全局 $3D$ 场景表示与 $2D$ 图像像素之间的 $2D$ 重投影误差，从而提高定位精度。在推理阶段，我们的模型可以估计出相机和全局坐标系下的 $3D$ 场景几何，并通过刚性配准它们来实时地获得姿态。我们在三个公开的视觉定位数据集上评估了我们的方法，进行了消融实验，并展示了我们的方法在所有数据集上都优于现有的姿态回归方法的姿态精度。

3. 方法详解¶

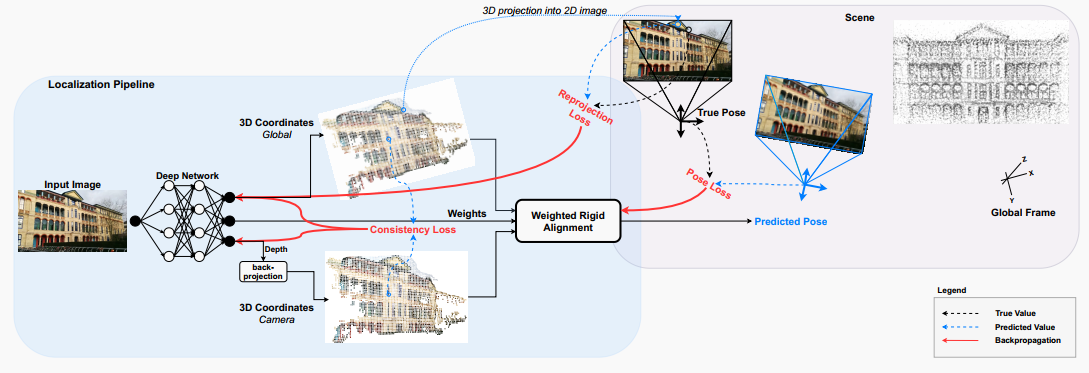
图2：我们的方法的流程图。

我们的方法使用全局相机姿态 $T$ 作为输入图像 $I$ 的监督标签，来训练一个深度神经网络，以学习场景的表示。

为此，我们将定位过程定义为获取一张图像作为输入，生成两组 $3D$ 点，每组在不同的坐标系统中。第一组是全局参考系中的一组 $3D$ 坐标 $G=\{\hat{g}_i，...，\hat{g}_M\}$。这些是由网络直接预测的。第二组是相机坐标系中的一组 $3D$ 坐标 $C=\{\hat{c}_i，...，\hat{c}_M\}$。 对于后者，网络预测深度，然后使用内参通过方程(6)进行反向投影以获得相机坐标系中的 $3D$ 坐标。 通过图像像素坐标，这两个 $3D$ 点云内在匹配。

使用刚性配准，可以通过对齐两个点云来估计姿态 $\hat{T}$。 为此，我们利用 Kabsch 算法。它是可微的，无参数的，并以闭式解的形式在单步中获得解决方案。 这使得过程端到端可训练。

为了考虑预测的不完美性，网络预测一组权重 $W=\{w_i，...，w_M\}$，用于评估每个 $3D$ 对应点对刚性配准的贡献大小。 给定这样的对应关系，然后应用加权 Kabsch 算法来估计从相机坐标系统到全局坐标系统的相对姿态。 给定 $M$ 个 $3D$ 坐标，该加权最小化目标定义为：

$\arg \min\limits_{\hat{R}，\hat{t}}\sum\limits_{i}^{M}w_{i}||\hat{g}_{i}-\hat{R}\hat{c}_{i}-\hat{t}||_{2}$，(1)

可以描述为：平移 $\hat{t}$ 通过居中两个点云来消除姿态的平移部分：

$\mu_{g}=\frac{\sum\limits_{i}w_{i}\hat{g}_{i}}{\sum\limits_{i}w_{i}}，\overline{G}=G-\mu _{g}$

$\mu_{c}=\frac{\sum\limits_{i}w_{i}\hat{c}_{i}}{\sum\limits_{i}w_{i}}，\overline{C}=C-\mu_{c}$。

然后通过奇异值分解(SVD)恢复旋转 $\hat{R}$ 和平移 $\hat{t}$：

$USV^{T}=svd(\overline{C}^{T}W\overline{G})$

$s=det(VU^{T})$

$\hat{R}=V\begin{pmatrix} 1 & 0 & 0\\ 0 & 1 & 0 \\ 0 & 0 & s \end{pmatrix}U^{T}$

$\hat{t}=-\hat{R}\mu_{c}+\mu_{g}$。

我们应用姿态损失以引导刚性配准，以使网络学习 $3D$ 几何表示。给定地面真实姿态 $T$，由旋转 $R$ 和平移 $t$ 组件组成，可以定义一个成本函数来最小化估计分量和地面真实分量之间的差异。我们将损失定义为位置损失和旋转损失的总和：

$L_{pose}=L_{position}+L_{rotation}$，(2)

其中,

$L_{position}=||t-\hat{t}||_{2}$，(3)

定义了计算出的平移 $\hat{t}$ 与实际平移 $t$ 之间的位置误差，且

$L_{rotation}=cos^{-1}(\frac{1}{2}(trace(\hat{R}R^{-1})-1))$(4)

度量计算出的旋转 $\hat{R}$ 与地面真实旋转 $R$ 之间的角度误差。

通过梯度下降预测的姿态被调整，在训练过程中，由姿态损失方程(2)引导，以匹配地面真实姿态，从而间接调整两个几何表示(3D 云)。所提出的表达方式允许包含额外的约束，这些约束可主动指导从姿态进行隐含 3D 几何表示的优化。因此，我们引入一致性损失来约束几何预测根据地面真实姿态对齐。我们首先使用地面真实姿态将相机坐标系中的 3D 点转换到全局坐标系中。一致性损失测量全局坐标系中的 3D 点 $G$ 与从相机坐标系转换的 3D 点 $C$ 之间的误差，使用地面真实姿态，我们将其称为一致性损失。我们将其定义为：

$L_{consistency}=\frac{1}{M}\sum\limits_{i}^{M}||\hat{g}_{i}-T\hat{c}_{i}||_{2}$，(5)

而不是直接预测 $3D$ 坐标，我们可以调整网络以预测深度。给定深度，其形成相机透视图中的 Z 坐标，给定相机内参，X 和 Y 直接从图像像素和深度获得。因此，相机坐标系中的 3D 点 $C$ 是通过根据方程(6)反投影深度获得的：

$\hat{c}_{i}=\hat{d}_{i}K^{-1}u_{i}$，(6)

其中 $u_i$、$K$、$\hat{d}_i$ 和 $\hat{c}_i$ 分别表示同质像素坐标、相机内参矩阵、深度和相应的相机坐标系中的点。

此外，通过利用重投影损失来最小化重新投影全局坐标系中的 3D 坐标与图像框架中的 2D 图像像素之间的误差，以进一步约束全局坐标中的 3D 坐标。其定义为：

$L_{reprojection}=\frac{1}{M}\sum\limits_{i}^{M}||u_{i}-\pi(T\hat{g}_{i})||_{2}$，(7)

其中 $\pi$ 将点从 3D 全局坐标系投影到图像坐标系中。

利用姿态标签和定义的表达方式，我们的方法隐式学习场景的几何表示。在推理时给定图像，所提出的方法估计场景的几何并将其用于姿态计算。

然后总损失是姿态损失、重投影损失和一致性损失的加权组合：

$L_{total}=\lambda_{p}L_{pose}+\lambda_{c}L_{consistency}+\lambda_{r}L_{reprojection}$，(8)

其中 $\lambda_{p}$、$\lambda_{c}$ 和 $\lambda_{r}$ 是损失加权因子。

4. 实验结果¶

本文在三个常用的视觉定位数据集上进行了实验，分别是剑桥地标数据集，7场景数据集和12场景数据集。这些数据集包含了不同的场景，如室内、室外、动态、静态等，以及不同的姿态变化，如旋转、平移、缩放等。本文使用了两种评价指标，分别是位置误差和方向误差。位置误差是指估计的相机位置和真实位置之间的欧氏距离，方向误差是指估计的相机方向和真实方向之间的角度差。实验结果表明，本文的方法在所有数据集上都超过了现有的回归方法的姿态精度。并且可以实时地从单张图像中估计出场景的三维几何信息，并通过对齐得到姿态。

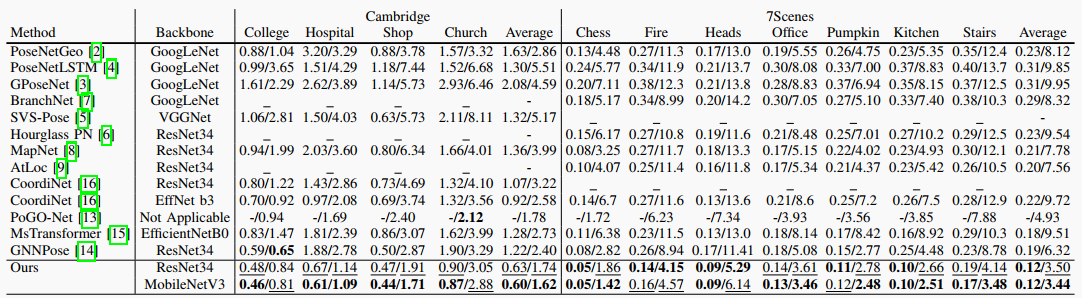
表I：我们的方法和最先进的定位方法在剑桥地标数据集和7场景数据集上的姿态误差的比较。

表II：我们的方法在剑桥地标数据集、7场景数据集和12场景数据集上的消融实验结果。

表III：不同的过滤方法对我们的方法的姿态精度的影响。

图3：在7Scenes数据集上的预测结果的可视化示例。

5. 结论¶

我们提出了一种新颖的方法，它可以从单个 RGB 图像进行全局 6 自由度姿态估计。我们的方法与大多数现有的姿态回归方法有相同的约束条件，即：从一组图像姿态对进行训练，从单个图像估计姿态，仅保存网络权重，并在实时内输出姿态。然而，我们的方法能够获得更准确的姿态估计，这是因为我们将几何信息纳入了姿态估计过程中。要实现这一点，我们面临的挑战是，如何利用仅给出的标签(姿态)来学习这种几何，以及如何在实时内利用几何来估计姿态。我们方法的主要创新之处在于，我们使用姿态目标来指导深度神经网络，通过可微分的刚性配准，学习场景几何，而不需要在训练时提供这种几何的显式地面真值。我们的方法接收单个图像作为输入，并仅使用姿态标签来隐式地学习场景的几何表示。这些隐式学习的几何表示是场景在两个参考系(全局坐标系和相机坐标系)下的三维坐标(X，Y，Z 坐标)。我们使用无参数和可微分的刚性配准，通过深度神经网络传递梯度，以调整其权重并持续地学习这些表示，而不需要这些量的显式地面真值标签。除了姿态损失之外，我们方法的另一个创新之处在于，它允许引入额外的学习损失，而这在仅进行姿态回归的定位过程中是不可行的。我们引入了一致性损失，使两个几何表示与几何姿态保持一致，并引入了重投影损失，以将全局坐标下的三维坐标约束到二维图像像素上。通过大量的实验，我们展示了我们的方法在定位精度上优于当前最先进的回归方法，并且可以实时运行。最后，我们展示了我们的方法可以利用部分标签(仅位置标签)来对预训练模型进行微调，从而改善定位和定向的性能。在未来的工作中，我们希望利用基础模型生成的嵌入，并将其集成到我们学习的三维表示中，以利用场景语义进行更精确的姿态估计。