ICCV2023论文精读：Self-Supervised Point Cloud Completion from Single Partial Clouds¶

A. 原文概要¶

点云补全是指根据部分点云恢复完整的点云形状。现有方法需要完整的点云或同一对象的多个部分点云来进行训练。与以前的方法形成对比，本论文提出的Partial2Complete (P2C)第一个仅需要每个对象的单个不完整点云就可以进行自监督学习的框架。具体而言，我们的框架将不完整点云分组为局部点云块作为输入，预测被遮挡的点云块，通过观察不同的局部对象学习先验信息。我们还提出了区域敏感Chamfer距离以正则化形状误匹配，不限制补全能力，并设计了法线一致性约束，鼓励恢复的形状表面连续完整。这样，P2C不再需要完整形状作为监督，而是从类别特定数据集中学习结构线索，补全部分点云。我们在人工ShapeNet数据和真实ScanNet数据上证明了我们方法的有效性，结果显示P2C产生了与完整形状训练方法可媲美的结果，并优于多视角训练的方法。

原文链接：https://arxiv.org/abs/2307.14726

B. 方案优势¶

本方法具有以下3个优势：

1)本方案消除了对完整样本的需求，从而减少了标注的困难和费用;

2)即使只有一个视角，也可以轻松地从真实世界中收集局部对象，大大扩展了训练数据的范围;

3)利用未知的不完整性假设，可以将部分样本、完整形状和弱监督线索统一到学习框架中，以改进补全质量。

下图展示了本方案与现有主要方案的区别。

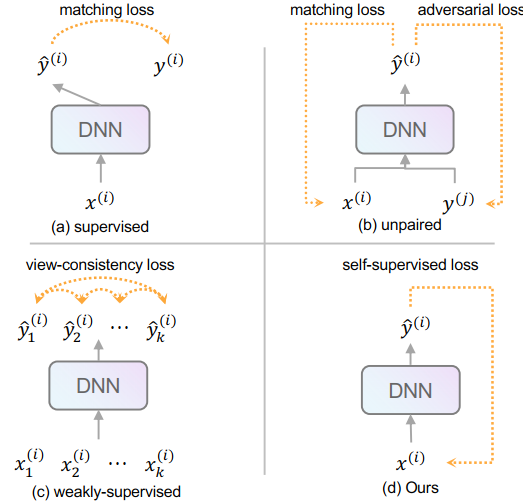
C. 背景介绍¶

点云被广泛用于3D形状表示，在目标检测和目标跟踪等领域中发挥关键作用。然而，真实世界的原始点云通常来自激光扫描仪和深度摄像头等设备，由于遮挡和光照条件变化，往往是不完整和带有噪声的。因此，人们开始研究点云补全，以从部分点云获得完整点云。

监督学习是最直接的解决方案，但它需要部分点云和对应的完整点云进行训练。然而，收集完整点云是有挑战的。因此，训练数据对通常通过在ShapeNet等3D模型上模拟遮挡获得。由于真实数据和模拟数据之间的分布差异，这些方法在真实场景鲁棒性往往受到限制。

弱监督点云补全是监督点云补全的替代方案，它使用仅包含部分形状的点云和同一类别的完整样本实例进行训练，因此不需要成对的部分和完整点集。所以，这种方法支持使用大规模真实扫描的不完整点云和虚拟3D物体数据集。但是，获得大规模、完整且干净的3D点云数据集仍有挑战，比如人工成本、设备费用等。 已提出弱监督方法，通过使用同一物体的多个未对齐观测构建弱监督线索进行训练。但是，这些方法的性能可能会严重受到对齐错误的影响；另外，由于硬件局限或视角限制，从多个视角收集观测点云也很困难。

为解决这些挑战，本文介绍了一种新的自监督点云补全方法，这种方法仅需要每个物体一个点云形状，该形状的不完整程度不受限制。

D. 理论介绍¶

上图展示了P2C的具体流程图。

本文介绍的Partial2Complete (P2C)是一个使用每个对象仅有的单个部分点云进行训练的点云补全网络。P2C将输入点分组为表示基础表面上一个小但可能连续区域的点云块，这些是希望网络可以预测的被遮挡的区域。本方法假设通过观察具有不同缺失部件的大量训练对象，可以学习出结构先验知识，指导严重不完整点云的重建。 此外，本方案利用未配对图像平移构建循环约束，为框架提供潜在重构损失。这种正则化确保完成同一物体的不同局部区域生成相同的完整形状。

本方案还提出了两个新的组件来解决自监督设置所特有的问题。首先，传统的点云距离度量缺乏对补全任务中出现的完整或缺失区域的认识，导致补全能力受限或预测不匹配。为解这个问题，作者引入了区域敏感Chamfer距离(RCD)，利用围绕动态生成的骨架点构建的局部区域估计点云对应关系。通过优化RCD，可能的异常点可以被拉向目标点集，不会受到补全缺失区域的限制。另一方面，受曲率基于表面几何的技术的启发，作者提出法线一致性约束(NCC)，它计算附近点的法线方向相似度，并将相似度方差作为正则项计算，鼓励生成的点遵循不完整点云的局部2D表面流形。简单来说，NCC是一种生成平滑表面的策略。

E. 方法详析¶

P2C网络¶

设$P_{p}$为不完整点云，$P_{c}$为$P_{p}$的预测补全。我们的框架以$P_{p}$为输入，生成M个点云块，每个点云块表示底层表面的一个小但可能连续的区域，这些事希望网络可以预测的被遮挡的点云块。 M个点云块被分割为三组{$G_{rec}$，$G_{com}$，$G_{latent}$}。$G_{rec}$是网络可观测的区域，我们强制网络生成预测点云$P_{c}$，在$G_{rec}$区域与输入相匹配，并引入重构损失$L_{r}$。尽管$L_{r}$有效地正则化预测形状与$G_{rec}$中的观测区域匹配，仅凭此无法指导网络预测完整形状。为此，我们使用补全损失$L_{c}$来惩罚网络无法预测被遮挡组$G_{com}$。人工遮挡的部分和输入中缺失的部分对网络都是未见的，因此最小化$L_{c}$可以指导网络同时补全自然缺失和有意遮挡的区域。

第一个组$G_{rec}$经过编码器产生潜在特征嵌入f，表示相应物体的编码，作为解码器的输入以产生形状预测$P_{c}$。为进一步正则化补全，我们引入潜在重构损失$L_{f}$，鼓励对象的两个不同局部区域集共享相同的物体潜在表示。特别是，我们利用第三组块$G_{latent}$，这种块独立于$G_{rec}$，不被编码器观察。通过对$P_{c}$中与$G_{latent}$相同的空间位置进行重采样，我们收集另一组块$\bar{G}_{latent}$。然后，我们传递$\bar{G}_{latent}$给编码器，得到潜在特征f'，$L_{f}$用来惩罚f和f'之间的差异。

点云块分区¶

我们从对象表面采样点云块，以提供局部区域的信息。为此，我们使用最远点抽样(FPS)在部分形状$P_{p}$上采样M个点作为块中心$C = {c_i}^M_{i=1}$，表示观察到的粗略形状。然后，我们根据欧几里德距离收集每个中心点的k近邻以获得块$g_i = {p|p∈N^{P_{p}}_{k(c_i)}}$，其中$N^{P_{p}}_{k}(c_i)$表示$P_{p}$中c_i的k近邻集。此外，块被划分为三个分区:$G_{rec}$，$G_{com}$和$G_{latent}$，比例为$r_1:r_2:r_3$。一旦解码器产生预测形状$P_{c}$，我们对$G_{latent}$中相应的区域进行重采样，采用与$G_{latent}$相同的块中心，并在$P_{c}$中搜索k近邻。

区域敏感Chamfer距离¶

Chamfer距离(CD)和单向Chamfer距离(UCD)是度量具有不同点数的两个点云之间距离的常用方法。S1和S2两个点集之间的UCD定义如下:

$d_{UCD}(S_1，S_2) = \frac{1}{|S_1|}\sum_{x\in S_1}\min_{y \in S_2}||x-y||_2$

通过UCD可以定义CD:$d_{CD}=d_{UCD}(S_1，S_2)+d_{UCD}(S_2，S_1)$

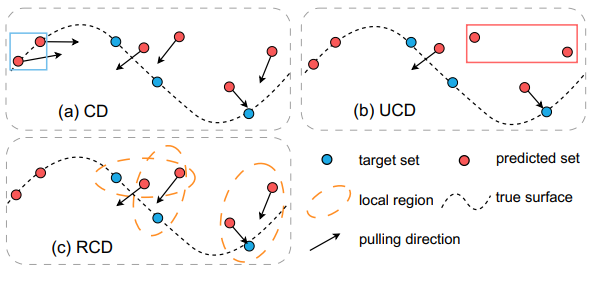
设$P_{p}$为一个具有某些缺失区域的部分点云，$P_{c}$为对应完整但可能有噪声形状的预测。在自监督补全中，我们没有访问完整形状作为真值，CD不考虑不完整性，而UCD对异常值没有正则化。对于$d_{CD}$($P_{p}$，$P_{c}$)，与未见部分对应的预测点p∈$P_{c}$被估计为远离底层表面的。因此，如上图(a)所示，蓝框中的两个点位于物体的真实表面上，但它们会被位移以最小化CD。因此，CD阻止网络推断缺失的部分。此外，$d_{UCD}$($P_{p}$，$P_{c}$)仅考虑预测中靠近$P_{p}$中的点的最近邻。我们在上图(b)中展示，尽管未见区域的补全不会受到限制，但红框中的异常点不太可能被选为目标集中点的最近邻，导致预测中的异常值没有距离度量。因此，使用UCD作为距离度量时，网络将学习在预测中避免异常值。

区域敏感Chamfer距离(RCD)通过围绕从部分形状$P_{p}$中动态采样的骨架点构建局部区域，解决见域/未见域的问题。具体地说，给定两个点集$P_{p}$和$P_{c}$，从$P_{p}$中通过最远点采样采样m个点作为骨架点$C = {c_i}^m_{i=1}$，表示观察到的粗略形状。然后，对每个骨架点收集每个点集中的k近邻，形成两个表示匹配区域的集合Rp和Rc。然后，RCD可通过UCD定义为:

$d_{RCD}(P_p，P_c)=d_{UCD}(R_p，R_c)+d_{UCD}(R_c，R_p)$

其中，

$R_p=\bigcup_{i=1}^{m}\{N_{P_p}^k(c_i)|c_i\in C\} \text{对} P_p$

$R_c=\bigcup_{i=1}^{m}\{N_{P_c}^k(c_i)|c_i\in C\} \text{对} P_c$

是$P_{p}$和$P_{c}$中所有骨架点的k近邻的并集。

法线一致性约束¶

为进一步正则化补全，我们引入法线一致性约束(NCC)改进表面连续性。

给定点云P = {$p_i$}$^n_{i=1}$，点pi的切平面法线方向的总最小二乘估计通过附近k个邻点$q_j$∈N$^P_{k}(pi)$的协方差矩阵Cov的特征值分解获得，其中

$Cov = \frac{1}{k}\sum_{j=1}^{k}(q_j-\hat{p})(q_j-\hat{p})^T， \hat{p} = \frac{1}{k}\sum_{j=1}^{k}q_j$

对应最小特征值的特征向量是估计的法线方向$v_i$，并归一化为||$v_i$||=1。我们定义点$p_i$的法线一致性为:

$nc(p_i) = \sqrt{\sum_{j=1}^{k}(v_i^Tv_j - \mu_i)^2}$

其中点积用作相似度测量，$\mu_i = \frac{1}{k}\sum_{j=1}^{k}v_i^Tv_j$是$v_i$与$v_j$之间相似度的均值。nc(·)的值表示法线相似度的方差，估计局部表面曲率。随着局部表面接近分段平面，nc(·)减小到0，而随着曲率增加，nc(·)增加。进一步，NCC定义为:

$NCC(P) = \frac{1}{n}\sum_{i=1}^{n}nc(p_i)$

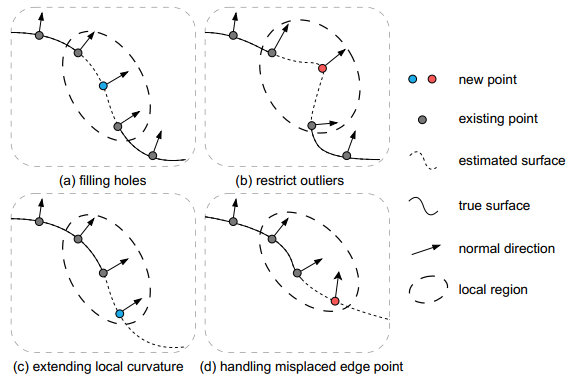
如上图所示，当新点遵循底层表面时，方差更小，而当新点导致表面偏离现有表面曲率时，方差更大。因此，NCC正则化预测更平滑，延长边缘点以使预测更完整，从而获得更好的形状补全。

优化¶

重构损失和补全损失定义为$L_{r}$ = dRCD($G_{rec}$，$P_{c}$)和$L_{c}$ = dRCD($G_{com}$，$P_{c}$)。我们将$P_{c}$中的$\bar{G}_{latent}$编码为潜在表示f'∈$R^d$，并通过潜在重构损失鼓励其与第一个潜在嵌入f∈$R^d$一致:

$L_f(f，f') = \frac{1}{d}\sum_{i=1}^{d}\varphi(f_i-f'_i)$

其中φ(·)是Huber损失。与NCC损失函数Lncc = NCC($P_{c}$)一起，我们有:

$L = \lambda_{rec}L_r + \lambda_{com}L_c + \lambda_{latent}L_f + \lambda_{ncc}L_{ncc}$

其中$λ_{rec}，λ_{com}，λ_{latent}，λ_{ncc}$是权重参数。

F. 文章总结¶

本文提出了P2C方法，这是第一个仅需要每个对象的单个不完整点云进行训练的自监督点云补全方法。本方法采用新颖的区域敏感Chamfer距离来测量输入预测相似性，并设计了法线一致性约束以增强预测的完整性。实验结果表明，P2C在人工和真实补全任务上都展现出优秀的性能，甚至优于使用完整点云进行训练的模型。总的来说，该方法为仅给定缺失点云数据的点云补全提供了有效解决方案。