【神经网络搜索】DARTS: Differentiable Architecture Search¶
【GiantPandaCV】DARTS将离散的搜索空间松弛,从而可以用梯度的方式进行优化,从而求解神经网络搜索问题。本文首发于GiantPandaCV,未经允许,不得转载。

1. 简介¶
此论文之前的NAS大部分都是使用强化学习或者进化算法等在离散的搜索空间中找到最优的网络结构。而DARTS的出现,开辟了一个新的分支,将离散的搜索空间进行松弛,得到连续的搜索空间,进而可以使用梯度优化的方处理神经网络搜索问题。DARTS将NAS建模为一个两级优化问题(Bi-Level Optimization),通过使用Gradient Decent的方法进行交替优化,从而可以求解出最优的网络架构。DARTS也属于One-Shot NAS的方法,也就是先构建一个超网,然后从超网中得到最优子网络的方法。
2. 贡献¶
DARTS文章一共有三个贡献:
- 基于二级最优化方法提出了一个全新的可微分的神经网络搜索方法。
- 在CIFAR-10和PTB(NLP数据集)上都达到了非常好的结果。
- 和之前的不可微分方式的网络搜索相比,效率大幅度提升,可以在单个GPU上训练出一个满意的模型。
笔者这里补一张对比图,来自之前笔者翻译的一篇综述:
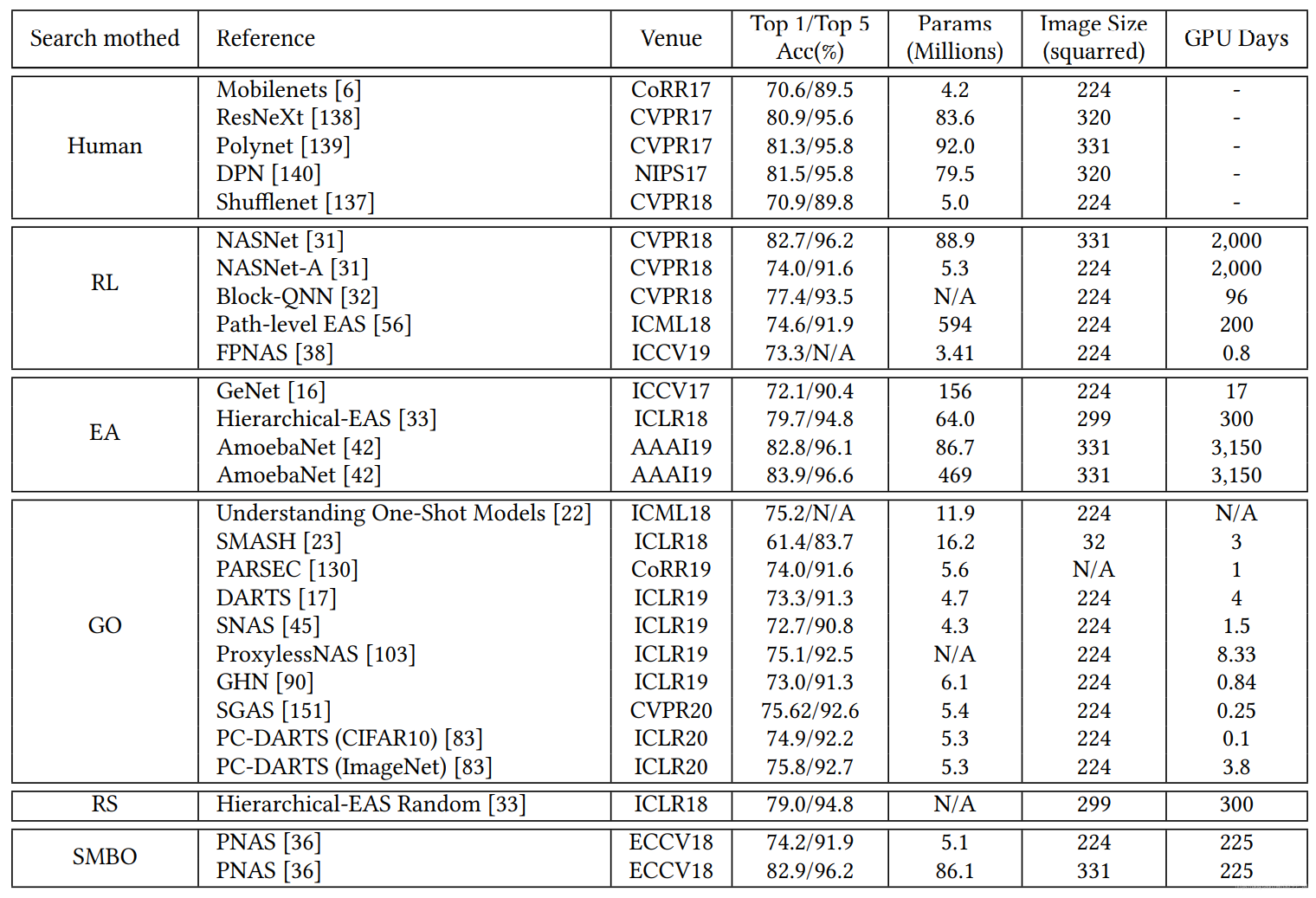
简单一对比,DARTS开创的Gradient Optimization方法使用的GPU Days就可以看出结果非常惊人,与基于强化学习、进化算法等相比,DARTS不愧是年轻人的第一个NAS模型。
3. 方法¶
DARTS采用的是Cell-Based网络架构搜索方法,也分为Normal Cell和Reduction Cell两种,分别搜索完成以后会通过拼接的方式形成完整网络。在DARTS中假设每个Cell都有两个输入,一个输出。对于Convolution Cell来说,输入的节点是前两层的输出;对于Recurrent Cell来说,输入为当前步和上一步的隐藏状态。
DARTS核心方法可以用下面这四个图来讲解。
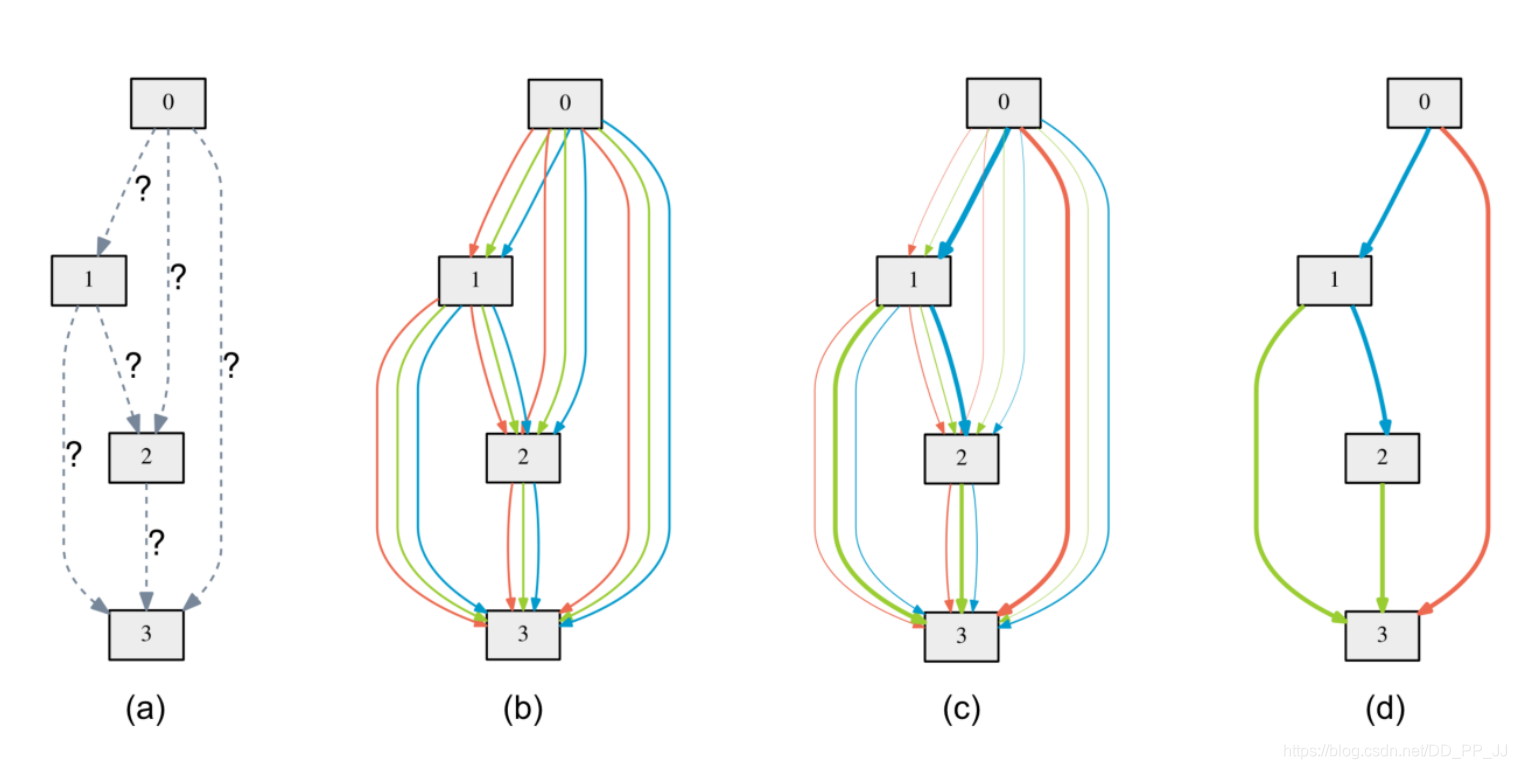
(a) 图是一个有向无环图,并且每个后边的节点都会与前边的节点相连,比如节点3一定会和节点0,1,2都相连。这里的节点可以理解为特征图;边代表采用的操作,比如卷积、池化等。
引入数学标记:
记 节点(特征图)为: x^{(i)} 代表第i个节点对应的潜在特征表示(特征图)。
记 边(操作)为: o^{(i,j)} 代表从第i个节点到第j个节点采用的操作。
记 每个节点的输入输出如下面公式表示,每个节点都会和之前的节点相连接,然后将结果通过求和的方式得到第j个节点的特征图。
记 所有的候选操作为 \mathcal{O}, 在DARTS中包括了3x3深度可分离卷积、5x5深度可分离卷积、3x3空洞卷积、5x5空洞卷积、3x3最大化池化、3x3平均池化,恒等,直连,共8个操作。
(b) 图是一个超网,将每个边都扩展了8个操作,通过这种方式可以将离散的搜索空间松弛化。具体的操作根据如下公式:
这个可以分为两个部分理解,一个是o(x)代表操作,一个代表选择概率 \frac{\exp \left(\alpha_{o}^{(i, j)}\right)}{\sum_{o^{\prime} \in \mathcal{O}} \exp \left(\alpha_{o^{\prime}}^{(i, j)}\right)},这是一个softmax构成的概率,其中\alpha_o^{(i,j)}表示 第i个节点到第j个节点之间操作的权重,这也是之后需要搜索的网络结构参数,会影响该操作的概率。即以下公式:
左侧代表当前操作的概率,右侧代表当前操作的参数。
©和(d)图 是保留的边,训练完成以后,从所有的边中找到概率最大的边,即以下公式:
4. 数学推导¶
DARTS将NAS问题看作二级最优化问题,具体定义如下:
w*(\alpha) 代表当前网络结构参数\alpha的情况下,训练获得的最优的网络结构参数。
第一行代表:在验证数据集中,在特定网络操作参数w下,通过训练获得最优的网络结构参数\alpha。
第二行表示:在训练数据集中,在特定网络结构参数\alpha下,通过训练获得最优的网络操作参数w。
条件:在结构确定的情况下,获得最优的网络操作权重
----- 结构确定,训练好卷积核
目标:在网络操作权重确定的情况下,获得最优的结构
----- 卷积核不动,选择更好的结构
最简单的方法是通过交替优化参数w和参数\alpha, 来得到最优的结果,伪代码如下:

交替优化的复杂度非常高,是O(|\alpha||w|), 这种复杂度不可能投入使用,所以要将复杂度进行优化,用复杂度低的公式近似目标函数。
这种近似方法在Meta Learning中经常用到,详见《Model-agnostic meta-learning for fast adaptation of deep networks》,也就是通过使用单个step的训练调整w,让这个结果来近似w*(\alpha)。
然后对右侧公式进行推导,得到梯度优化以后的表达式:
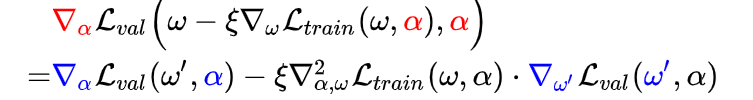
这里求梯度使用的是链式法则,回顾一下:
则梯度计算为:
或者
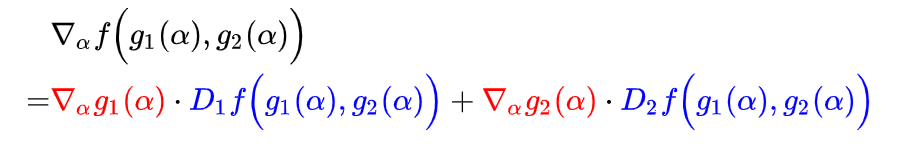
上述公式中Di代表对f(g1(\alpha),g2(\alpha))的第i项的偏导。

整理以后结果就是:
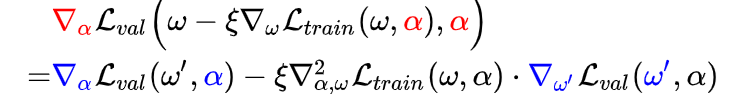
减号后边的是二次梯度,权重的梯度求解很麻烦,这里使用泰勒公式将二阶转为一阶(h是一个很小的值)。
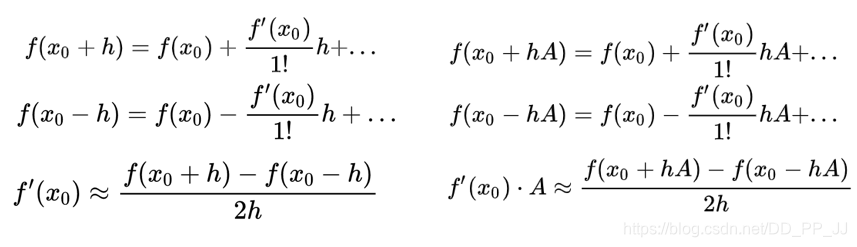
利用最右下角的公式:
令A=\nabla_{\omega^{\prime}} \mathcal{L}_{v a l}\left(\omega^{\prime}, \alpha\right),h=\epsilon, x_0=w, f=\nabla_{\alpha} \mathcal{L}_{\text {train }}(\cdot, \cdot), 代入可得(其中经验上设置\epsilon=\frac{0.01}{||\nabla_{w'}\mathcal{L}_{val}(w',\alpha)||_2})
其中
这样就可以将二次梯度转化为多个一次梯度。到这里复杂度从O(|\alpha||w|)优化到O(|\alpha|+|w|)
一阶近似: 当\xi=0, 下面式子的二阶倒数部分就消失了,这样模型的梯度计算可能不够准确,效果虽然不如二阶,但是计算速度快。只需要假设当前的w就是w*(\alpha), 然后启发式优化验证集上的loss值即可。
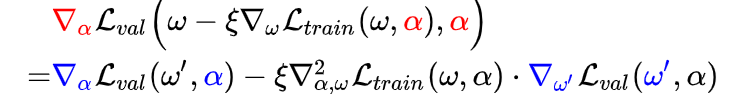
代码实现上也有一定的区别,代码将在下一篇讲解。
5. 实验设置¶
这里我们暂且先关注CIFAR10上的实验效果。DARTS构成网络的方式之前已经提到了,首先为每个单元内布使用DARTS进行搜索,通过在验证集上的表现决定最好的单元然后使用这些单元构建更大的网络架构,然后从头开始训练,报告在测试集上的表现。
CIFAR10上搜索操作有:
- 3x3 & 5x5 可分离卷积
- 3x3 & 5x5 空洞可分离卷积
- 3x3 max & avg pooling
- identiy
- zero
实验详细设置:
- 所有操作的stride=1, 为了保证他们空间分辨率,使用了padding。
-
卷积操作使用的是ReLU-Conv-BN的顺序,并且每个可分离卷积会被使用两次。
-
卷积单元包括了7个节点,输出节点为所有中间节点concate以后的结果。
- 网络整体深度的⅓和⅔处强制设置了reduction cell来降低空间分辨率。
- 网络结构参数\alpha_{\text{normal}}是被所有normal cell共享的,同理\alpha_{\text{reduce}}是被所有reduction cell共享的。
- 并没有使用全局batch normalization, 使用的是batch-specific statistic batch normalization
- CIFAR10一半的训练集作为验证集。
- 8个单元的消亡了使用DARTS训练50个epoch, batch size设置为64, 初始通道个数为16。
- 使用momentum SGD来优化权重,初始学习率设置为0.025,momentum 0.9 weight decay为0.0004.
- 网络架构参数\alpha 使用0作为初始化,使用Adam优化器来优化\alpha参数,初始学习率设置为0.0004,momentum为(0.5,0.999)weight decay=0.001。
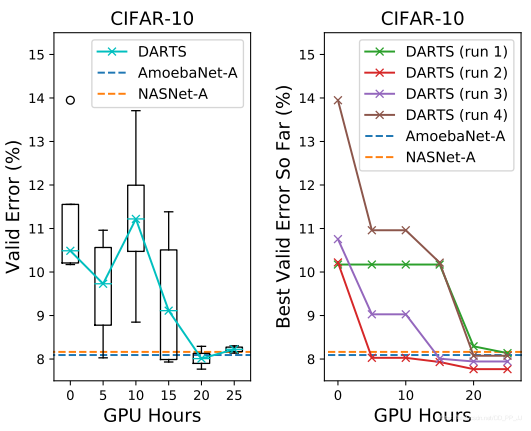
可以看到,搜索结果最终是优于AmoebaNet-A和NASNet-A。具体搜索得到的Normal Cell和Reduction Cell可视化如下:
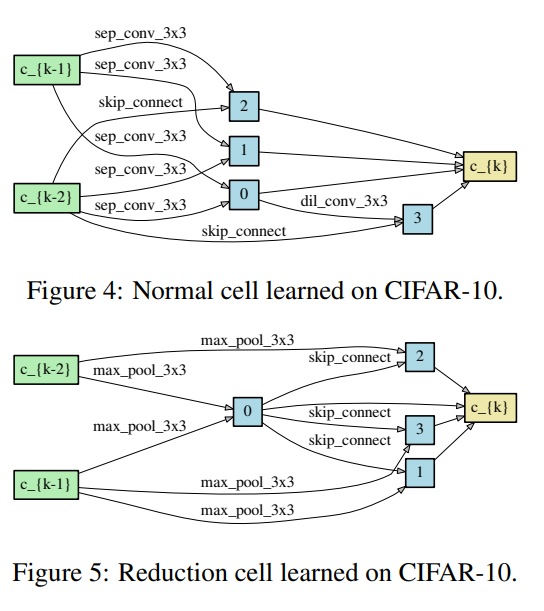
网络评价
网络优化对初始化值是非常敏感的,为了确定最终的网络结构,DARTS将使用随机种子运行四次,每次得到的Cell都会在训练集上从头开始训练很短一段时间大概100 epochs , 然后根据验证集上得到的最优结果决定最终的架构。
为了验证被选择的架构:
- 随机初始化权重
- 从头开始训练
- 报告测试集上的模型表现
CIFAR10搜索的模型迁移到ImageNet更多细节:
- 20个单元的大型网络使用了96的batch size, 训练了600个epoch
- 初始通道个数由16修改为36,为了让模型的参数和其他模型参数量相当。
- 其他参数设置和搜索过程中参数一样
- 使用了cutout的数据增强方法,以0.2的概率进行path dropout
- 使用了auxiliary tower(辅助头,在这里施加loss, 提前进行反向传播,InceptionV3中提出)
- 使用PyTorch在单个GPU上花费1.5天时间训练完ImageNet,独立训练10次作为最终的结果。
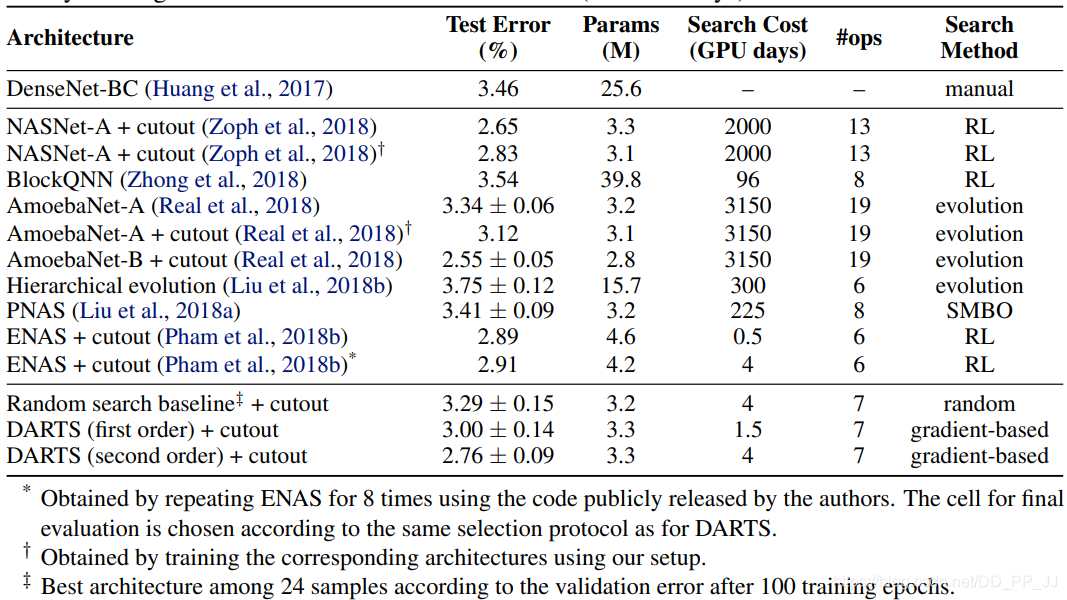
使用二阶优化方法+cutout的数据增强方法,DARTS能达到约2.76的准确率,笔者使用nni进行了实验,最终结果是2.6%的Test Error。
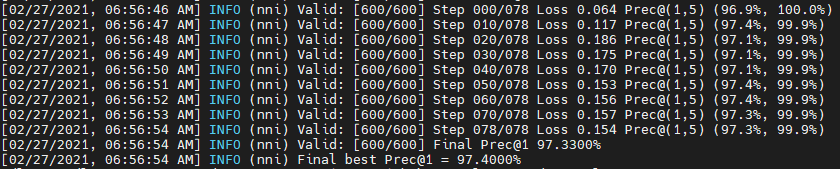
6. 致谢&参考¶
感谢师兄提供的资料,以及知乎上两位大佬,他们文章链接如下:
薰风读论文|DARTS—年轻人的第一个NAS模型 https://zhuanlan.zhihu.com/p/156832334
【论文笔记】DARTS公式推导 https://zhuanlan.zhihu.com/p/73037439
本文总阅读量次