跳转至

前言

近期大火的视觉Transformer使用自注意力机制对所有图像patch进行交互，能够灵活地对图像数据进行建模。然而自注意力机制本身O(n^2)的复杂度让其难以处理长序列或高分辨率图像。

我们基于key和query的互协方差矩阵，提出一个转置版本的自注意力操作(协方差注意力)，让其在token维上的操作转变成特征维上的操作，进而降低自注意力复杂度为线性增长。这种改进也让Xcit能够高效地处理高分辨率图像。

论文：https://arxiv.org/pdf/2106.09681.pdf 代码：https://github.com/facebookresearch/xcit

回顾原始self attention

给定一个形状为(N, d)的输入X，其中N代表token数量，d代表通道数。自注意力机制先通过三个独立的线性操作得到Q,K,V

Q = XW^Q, K = XW^K, V = XW^V

然后使用Q,K得到注意力特征图

A(K, Q) = Softmax(\frac{QK^T}{\sqrt{d_k}})

最后与V相乘

Attention(Q, K, V) = A(K, Q)V

我们着重看计算注意力特征图的部分，Q是一个N,d的矩阵，转置后的K是一个d,N。这两个矩阵相乘后得到N, N的矩阵，得到N^2个元素，每个元素需要d次相乘，因此复杂度是O(N^2d)。(更详细复杂度分析可参考公众号的Transformer综述)。

Gram矩阵和协方差矩阵的联系

未归一化的协方差矩阵可以写为C = X^TX，而格拉姆矩阵其实就是矩阵内积，即G = XX^T，格拉姆矩阵一般在风格迁移用的比较多，本质上就是计算向量之间的相关度。

而这两个矩阵的特征向量可以互相计算得到，如果V是G的特征向量，那么C的特征向量U可以由U=XV计算得到。

原始的自注意力计算过程可以看作是类似格拉姆矩阵的计算过程：

QK^T = XW_qW_k^TX^T

我们考虑使用互协方差矩阵的形式去替代，即：

K^TQ = W_k^TX^TXW_q

这样可以把复杂度减少O(Nd^2)

互协方差注意力

互协方差注意力公式如下：

XC_{Attention}(Q, K, V) = V*Softmax(\frac{K^TQ}{\tau})

l2norm和缩放

为了让计算的互协方差矩阵元素值在(-1, 1)这个范围内，我们先对Q, K都做了一个L2归一化，这能够加强训练的稳定性。

这么做虽然能保证稳定，但也限制了特征表达(比如某些特征比较突出，但是经过归一化后，该特征在数值上则没有那么大)，所以引入了一个可学习参数\tau来进行缩放。

Block-diagonal协方差注意力

与原始的多头注意力机制相似，受Group Normalization启发，我们并没有让所有特征互相交互，而是对其分组，对每个头单独应用协方差注意力

W_q(h,d,d_q), W_k(h,d,d_k), W_v(h,d,d_v)

其中d_q=d_k=d_v=d/h，这么做有两个好处

  • 注意力复杂度能够进一步通过h来控制
  • 这种分组的形式能更容易被优化，提升性能

相关代码如下：

class XCA(nn.Module):
    def __init__(self, dim, num_heads=8, qkv_bias=False, qk_scale=None, attn_drop=0., proj_drop=0.):
        ...

    def forward(self, x):
        B, N, C = x.shape
        qkv = self.qkv(x).reshape(B, N, 3, self.num_heads, C // self.num_heads)
        qkv = qkv.permute(2, 0, 3, 1, 4)
        q, k, v = qkv[0], qkv[1], qkv[2]   # make torchscript happy (cannot use tensor as tuple)

        # 转置
        q = q.transpose(-2, -1)
        k = k.transpose(-2, -1)
        v = v.transpose(-2, -1)

        q = torch.nn.functional.normalize(q, dim=-1)
        k = torch.nn.functional.normalize(k, dim=-1)

        attn = (q @ k.transpose(-2, -1)) * self.temperature
        attn = attn.softmax(dim=-1)
        attn = self.attn_drop(attn)

        x = (attn @ v).permute(0, 3, 1, 2).reshape(B, N, C)
        x = self.proj(x)
        x = self.proj_drop(x)
        return x

复杂度分析

原始的自注意力时间复杂度为O(N^2d)，显存复杂度为O(hN^2+Nd)

而互协方差注意力可把复杂度分别降为O(Nd^2/h), O(d^2/h+Nd)

其他组件

Local Patch interaction

使用了两个3x3的depthwise卷积+BN+GELU的组合，来增加局部Patch的交互。

FFN

跟原始的Vision Transformer保持一致结构

Global aggregation with class attention

采用CaiT的做法，在最后两层引入一个叫class attention的结构，跟注意力是一样的结构，只不过引入了一个class embedding，只有这个class embedding接如后面的FFN，完成分类的任务。

首先我们给x拼入一个class token

x = [cls\_token, x]

跟计算注意力一样，我们得到Q,K,V，但是对于Q，我们只取其中的第一个元素，也就是输入X中的class_token得到的Qc

Qc = W_q x_{cls\_token}

接着就是和自注意力机制一样的计算过程，由于只更新这个class_token相关的部分，所以计算的结果和输入x[1:] (因为输入x第一个元素是我们的class_token)拼接在一起，相关伪代码如下：

self.cls_token = nn.Parameter(...) # 得到class token 
x = torch.cat((cls_tokens, x), dim=1) # 拼接到x上

# Class Attention
def forward(...): 
  # 得到Q, K, V
  qc = q[:, :, 0:1]   # 取到 CLS token
  attn_cls = (qc * k).sum(dim=-1) * self.scale
  attn_cls = attn_cls.softmax(dim=-1)
  attn_cls = self.attn_drop(attn_cls)

  cls_tkn = (attn_cls.unsqueeze(2) @ v).transpose(1, 2).reshape(B, 1, C)
  cls_tkn = self.proj(cls_tkn)
  x = torch.cat([self.proj_drop(cls_tkn), x[:, 1:]], dim=1) # 重新拼回输入
  return x

实验结果

实验结果

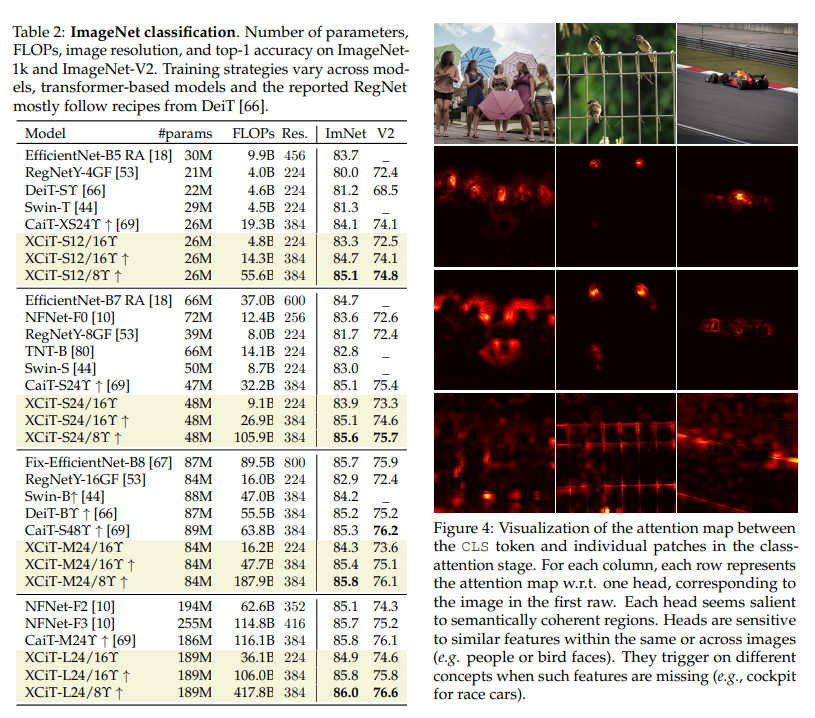
这种"取巧"的设计结构，让XCiT能更好地处理不同分辨率的图片，同时效果也是十分不错的。更多实验结果可以翻看原文。

总结

作者从互协方差矩阵和格拉姆矩阵之间的联系，结合自注意力复杂度高的原因，进而推导出一个极为简单的注意力转置形式，能够让复杂度从序列数量的平方变为特征的平方，在这一前提下减少特征数便可以大大减小模型参数。希望后续的视觉Transformer能够探索怎么能够像CNN一样，在不同分辨率下能够直接迁移预训练好的模型使用。

欢迎关注GiantPandaCV, 在这里你将看到独家的深度学习分享，坚持原创，每天分享我们学习到的新鲜知识。( • ̀ω•́ )✧

有对文章相关的问题，或者想要加入交流群，欢迎添加BBuf微信：

二维码

本文总阅读量次