AffineQuant 大语言模型的仿射变换量化

AffineQuant: Affine Transformation Quantization for Large Language Models¶

1. 论文信息¶

2. 引言¶

本文研究了大型语言模型（LLMs）在移动和边缘设备上的推理加速问题，这一问题在现实应用中具有重要意义。随着大型语言模型在多种任务中展现出卓越的性能，它们吸引了越来越多的关注。然而，这些模型通常需要庞大的计算资源，尤其是在训练和推理阶段。特别是在资源受限的移动和边缘设备上，模型的高效推理显得尤为重要。为此，研究者们寻求通过压缩技术，如量化，来减少模型的存储需求和计算负担。量化是一种有效的方法，通过将权重和激活映射到低比特表示来实现。

然而，量化经常会带来性能损失，尤其是在模型较小或使用低比特设置时。因此，后训练量化（PTQ）成为了一种受到关注的策略，它允许在不进行模型重训练的情况下进行优化，但这需要巧妙地处理量化过程中的误差和信息损失。文章中提到的一些创新方法，如AWQ、Omniquant和RPTQ，都是在寻找如何通过改进的量化策略来保持或甚至提升量化后的模型性能。

具体来说，本文提出了一种等价仿射变换的新方法，用于后训练量化中。该方法通过左乘仿射变换矩阵到线性层的权重，并右乘激活的逆矩阵，优化仿射变换矩阵，以减少量化误差。这种方法不仅能够提高模型在低比特量化配置下的表现，而且保证了转换矩阵在优化过程中的可逆性，利用Levy-Desplanques定理确保仿射矩阵的严格对角占优。通过这种方式，研究团队能够在有限的校准数据情况下稳定高维矩阵的优化，最终在不增加额外计算开销的情况下，实现了在各种模型配置上的最佳性能。

这些贡献不仅推动了量化技术的发展，使得大型语言模型能够在计算资源受限的环境下部署，还提供了一种新的优化算法，有效地扩展了模型在边缘设备上的应用范围，同时提升了模型在低比特配置下的精度和效率。这些研究成果对推动大型语言模型在实际应用中的广泛部署具有重要的理论价值和实际意义。

3. 方法¶

3.1 AffineQuant¶

AffineQuant 是一种利用仿射变换来优化后训练量化（PTQ）的方法，它在大型语言模型（LLMs）中应用，以减少量化误差并保持模型性能。此方法特别关注于如何通过仿射变换矩阵优化权重分布，从而适应量化函数的噪声特性，并通过这种方式减少引入的量化误差。

在数学表述中，AffineQuant 主要涉及两个操作：

1. 权重的仿射变换：$\mathcal{Q}(AW)$ 其中$A$ 是仿射变换矩阵，(W$ 是权重矩阵，(\mathcal{Q}(\cdot)$ 表示量化函数。这一步通过左乘权重矩阵$W$ 以$A$ 来更好地对齐权重分布与量化函数，从而扩展优化空间，使得在变换后的权重中的量化误差减少。

2. 激活值的仿射变换逆运算：$XA^{-1}$这里$X$ 是激活值，(A^{-1}$ 是仿射变换矩阵$A$ 的逆。通过右乘激活值$X$ 以$A$ 的逆，保持激活值和权重之间矩阵乘法输出的不变性。

核心的优化问题可以表达为： $<span><span class="MathJax_Preview">argmin_{A} \left \| XW - XA^{-1}\mathcal{Q}(AW) \right \|_F^2,</span><script type="math/tex">argmin_{A} \left \| XW - XA^{-1}\mathcal{Q}(AW) \right \|_F^2,$ 其中$\|\cdot\|_F$ 表示Frobenius范数，这个优化目标是为了最小化量化前后输出的均方误差，从而直接优化模型的性能指标如困惑度（perplexity）。

AffineQuant 结合了传统的量化技术中的尺度（scale）和位移（shift）变换，并引入了旋转等更高维的变换，使其能够在保持计算效率的同时，提供更精细的控制以适应不同的量化需求。通过这种方法，可以有效地处理量化过程中的信息损失，特别是在使用低比特宽度时。AffineQuant 还考虑到了仿射变换矩阵的可逆性，确保在优化过程中矩阵始终保持可逆，这是通过使用诸如Levy-Desplanques定理等数学定理来保证的。通过这种方式，AffineQuant 不仅能够减少模型在量化后的性能损失，而且能够扩展模型在边缘设备上的应用，为大型模型的部署提供了新的可能性。

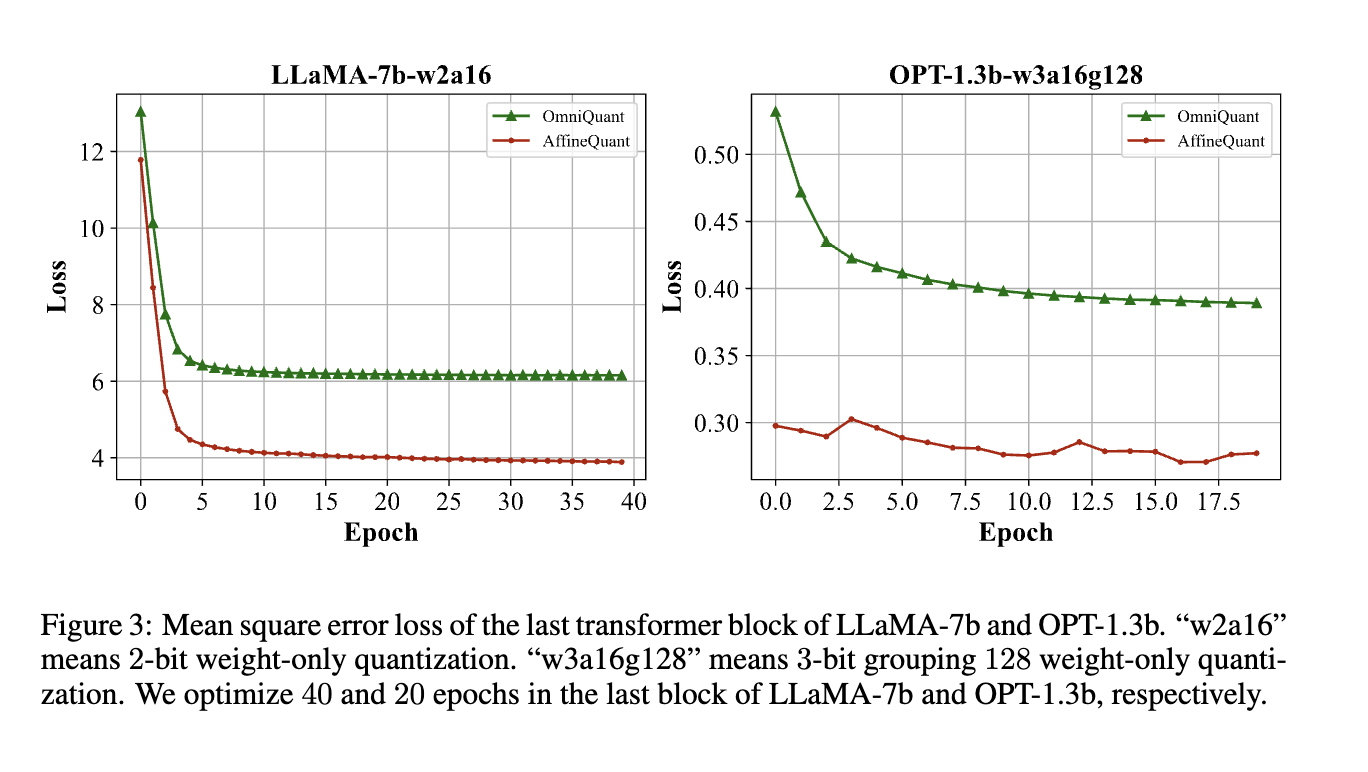
3.2 Reversibility and Gradual Mask¶

在仿射变换的上下文中，可逆性主要涉及确保优化过程中仿射变换矩阵的可逆性。关键是保持矩阵为严格对角占优矩阵，根据Levy-Desplanques定理，这保证了其可逆性。

严格对角占优矩阵： 如果对于每一行$ i $，对角线元素$ a_{ii} $ 的绝对值大于该行中所有非对角线元素的绝对值之和，那么矩阵$ A $ 被视为严格对角占优： $$ |a_{ii}| > \sum_{j \neq i}|a_{ij}|. $$ 通过确保矩阵$ A $ 在初始化时是严格对角占优的，并控制其更新，可以保持其在优化过程中的可逆性，这对于量化的稳定性和有效性至关重要。

渐进掩码¶

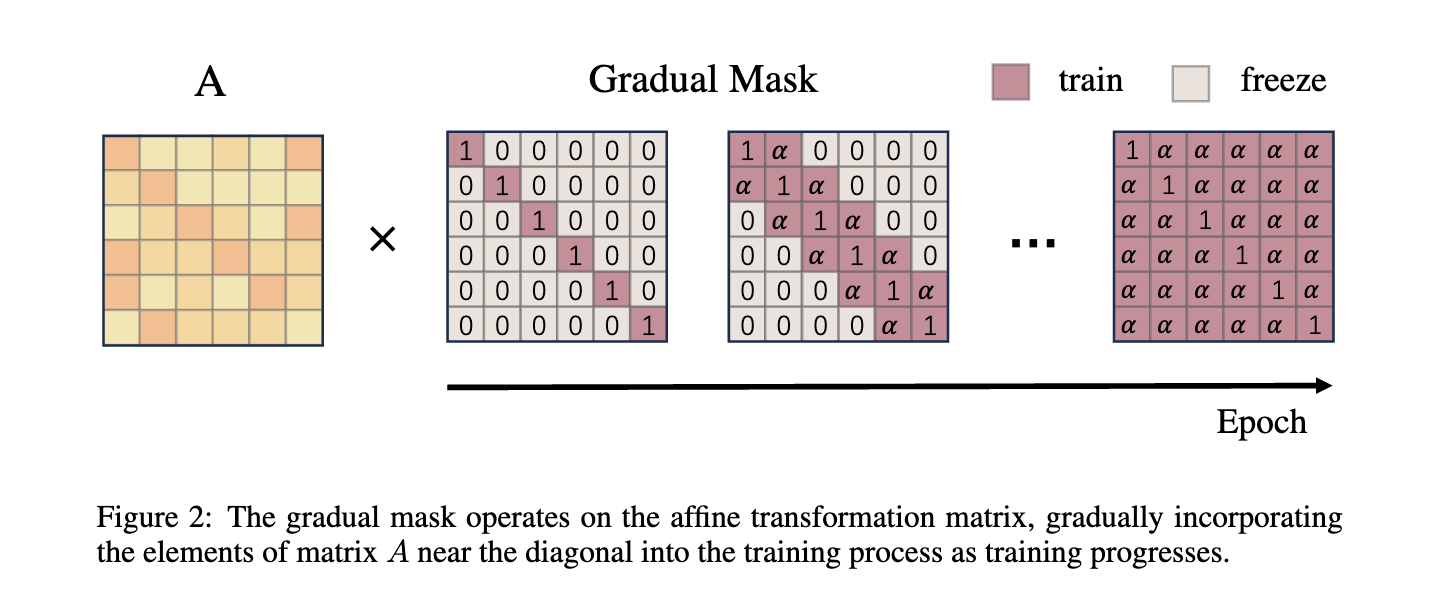
渐进掩码（GM）技术在优化过程中用来控制仿射变换矩阵的更新，特别是为了保持其严格对角占优属性并确保可逆性。这通过控制矩阵元素的暴露于优化过程来实现：

矩阵元素的渐进暴露： 渐进掩码开始时冻结所有元素，除了主对角线上的元素。随着优化的进行，靠近对角线的元素逐渐解冻，允许阶段性地将非对角线元素纳入优化过程中： $$ GM_{ij} = \begin{cases} 1 & \text{如果 } i = j, \ \alpha & \text{如果 } 0 < |i-j| \leq \frac{e}{t} \times \text{隐藏大小}, \ 0 & \text{其他情况}, \end{cases} $$ 其中$ \alpha $ 是稳定因子，$ t $ 是总周期数，$ e $ 是当前周期。这种方法通过允许靠近对角线的元素先适应和稳定，再逐步包含更远的元素，有助于有效管理学习率。

在优化中的实现¶

渐进掩码在优化过程中的实现具体如下：

1. 前向传播：

2. 矩阵$ A $ 与渐进掩码$ GM $ 进行元素乘积，有效地减小非主要元素的更新幅度： $$ A^{*}{e} = A{e} \circ GM_{e}, $$ 其中$\circ $ 表示哈达玛积。

3. 反向传播：

4. 应用更新时考虑渐进掩码，这影响学习率： $$ A_{e+1} = A_{e} + \eta GM_{e} \frac{\partial L}{\partial A^{*}_{e}}, $$ 确保更新尊重维持矩阵严格对角占优条件的需要。

这些过程确保了仿射变换矩阵在有效和稳定的优化过程中保持适用性，从而提升了整体量化性能并保持了可逆性。

3.3 Efficiency¶

文章讨论了通过优化仿射变换矩阵在模型量化中提升计算和推理效率的策略。

计算效率¶

使用PyTorch的线性代数库来进行仿射变换矩阵的逆运算，支持单精度和双精度格式。在优化过程中，模型的精度被维持为单精度或双精度，这是为了确保计算过程中的数值精度和效率。然而，由于计算机数值精度的限制，近似计算矩阵的逆可能会引入错误。因此，文中分析了两种精度类型在内存消耗、优化时间、错误量级和对模型性能的影响，具体结果将在后续的消融研究部分进行展示。

推理效率¶

为了提高模型在量化后的推理效率，研究者们将仿射变换矩阵与其他层（如线性层和LayerNorm层）的权重和偏置参数融合。在所有线性层中，仿射变换矩阵直接与权重和偏置参数合并，而在LayerNorm层中，由于存在高维信息，仅优化仿射矩阵的对角元素后进行合并。这种方法允许在不引入任何额外开销的情况下实现AffineQuant，使模型在保持高效推理的同时，也保证了量化的精度。

在量化实现中，尽管引入了额外的操作，例如在LayerNorm层的输出激活上应用二次量化，AffineQuant方法仍能在半精度推理中保持与其他算法相当的速度，展示了其高效性。

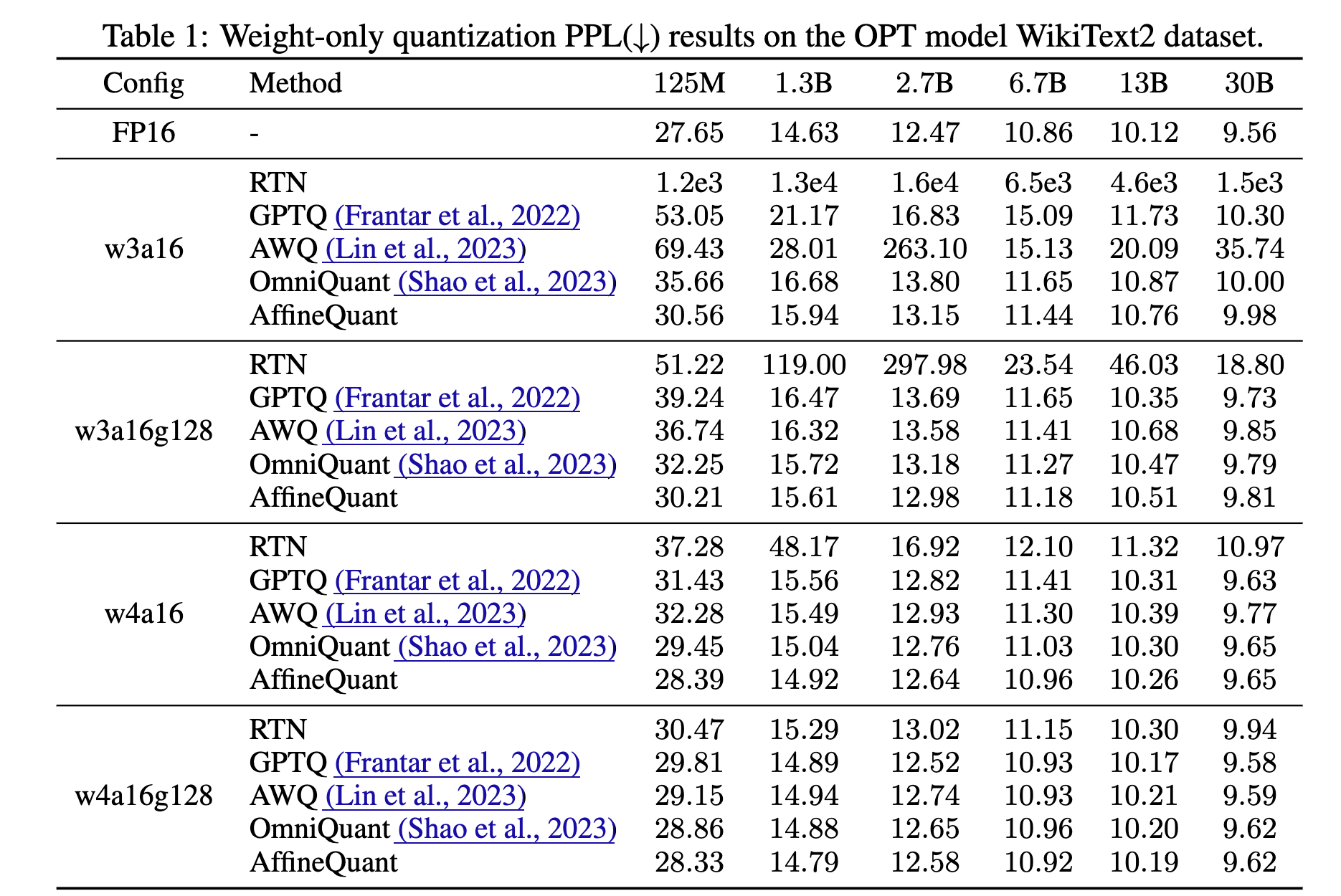
表格中展示了使用4位权重和4位激活量化配置时，AffineQuant在各种任务和复杂度模型上相比其他方法具有更优的性能，特别是在零样本任务和困惑度（PPL）任务中的表现。这些数据证明了AffineQuant在保证量化精度的同时，也优化了推理效率，这对于部署到资源受限的设备上尤为重要。

4. 实验¶

在本论文中，对不同精度方案下的模型性能、内存使用情况、优化运行时间以及合并误差进行了详尽的测试和比较。从实验结果可以看出，使用双精度(double)和单精度(float)方案相比于半精度(FP16)会显著增加内存使用和运行时间。例如，在OPT-125M模型上，双精度方案的内存使用量和运行时间是FP16的数倍，虽然其合并误差极小（约为$1.88$e$-16$），但PPL（困惑度）相比FP16有所增加。同样，单精度方案和混合精度(float-double)方案也展现了类似的趋势，内存和运行时间减半，但PPL和合并误差略有上升，说明在保持精度的同时减少计算资源的消耗是一个挑战。此外，论文还探讨了不同稳定性因子对模型性能的影响。结果显示，随着稳定性因子的减小（从$1$e$0$到$1$e$-8$），PPL普遍增加，特别是在更小的稳定性因子下，PPL的增加更为显著。例如，在OPT-125M模型上，稳定性因子为$1$e$-2$​时的PPL比FP16的PPL高出大约两倍。这一结果表明，在降低计算复杂性的同时保持或提升模型性能需要精心设计稳定性因子。整体而言，这些实验结果揭示了在降低模型精度和优化计算资源使用的过程中存在的权衡和挑战。尽管降低精度可以减少内存使用和加快运行时间，但这往往以牺牲模型的准确性和稳定性为代价。因此，未来的工作可能需要在保证模型性能的前提下，探索更有效的方法来降低模型运行的资源消耗。

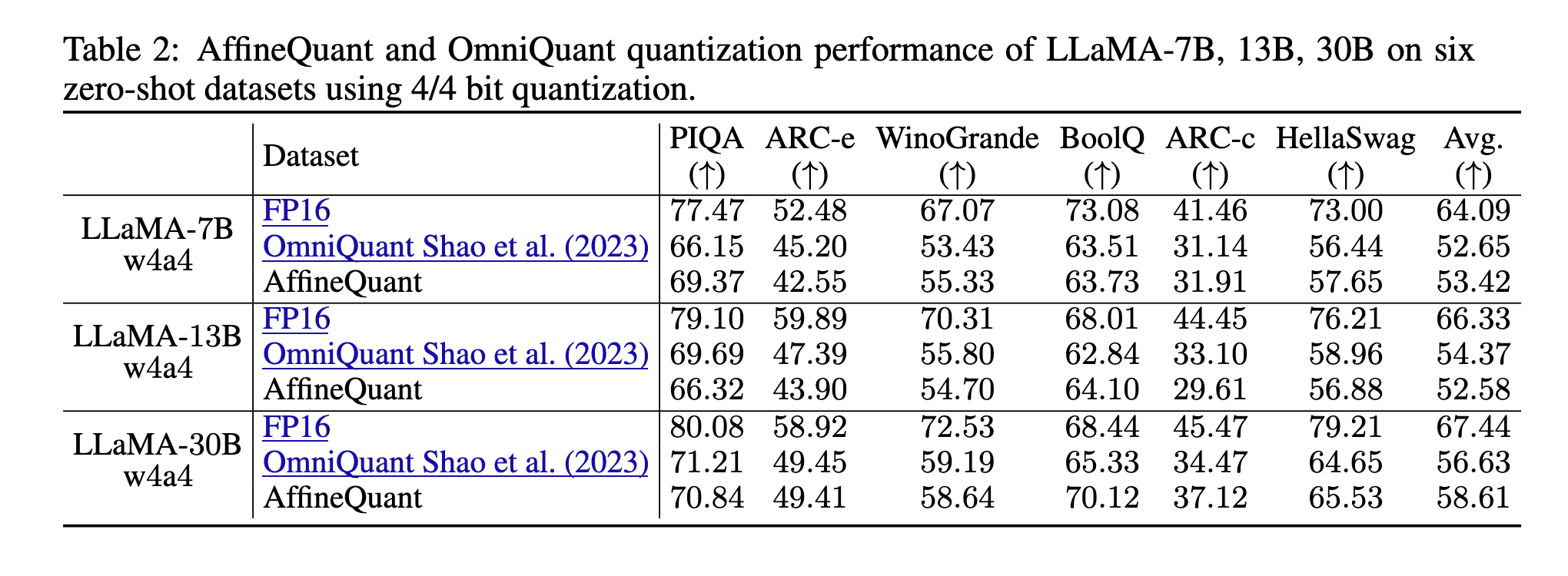
根据提供的实验数据，可以看出逐渐引入mask（gradual mask）的策略在两个模型（OPT-125M和LLaMA-7B）上对模型性能有显著影响。在没有采用逐渐mask策略的情况下，模型的性能明显下降，这在困惑度（PPL）的显著提高中体现得非常明显。对于OPT-125M模型，当没有使用逐渐mask时，WikiText2、PTB和C4的PPL分别高达$53.52$、$90.47$和$62.17$，而使用逐渐mask时这些值分别减少至$32.10$、$39.85$和$29.97$。这表明，逐渐mask对于控制模型在处理这些数据集时的困惑度有显著帮助，从而提升了模型的总体性能。在LLaMA-7B模型上，同样观察到类似的趋势。在使用逐渐mask的情况下，WikiText2和C4的PPL分别为$9.53$和$14.89$，而未使用时数据未给出，但可以推测其PPL可能会显著高于使用mask的情况。这一假设基于OPT-125M模型在没有使用逐渐mask时的性能显著下降。总的来说，逐渐mask策略显著提高了模型在特定文本数据集上的处理能力，有效减少了困惑度，改善了模型的稳定性和预测准确性。这一策略为处理复杂数据集提供了一种有效的优化手段，值得在未来的模型训练中继续探索和应用。

5. 讨论¶

优点¶

1. 提升计算效率： 通过保持模型在整个优化过程中的精度为单精度或双精度，以及利用PyTorch的线性代数库进行高效的矩阵逆计算，有效地提升了计算效率。这种做法减少了因精度转换带来的计算负担和潜在的数值误差。

2. 优化推理效率： 将仿射变换矩阵与模型的其他层（如权重和偏置）进行融合，特别是在LayerNorm层中只优化对角元素后进行融合，减少了模型推理过程中的计算复杂度和内存需求，从而提高了推理速度。

3. 维持或提升量化后的模型性能： 如表格所示，即便在较低的位宽（例如4/4位量化）下，AffineQuant方法在多个性能指标上仍然优于或接近全精度模型的表现，显示出较好的量化抗性和模型鲁棒性。

缺点¶

1. 数值精度的挑战： 即使使用高效的库和精细的精度控制，近似计算矩阵逆仍可能引入不可忽视的数值误差。这些误差可能会在特定的任务或数据集上影响模型的最终性能。

2. 复杂的实现细节： 虽然论文中描述了将仿射变换矩阵融合到其他层的方法，但实际实现这一过程可能涉及复杂的编程挑战，特别是在处理大规模模型和数据集时。此外，优化LayerNorm层中仅对角元素的策略可能不适用于所有类型的模型结构。

3. 硬件依赖性： 高效的仿射变换矩阵和其量化实现可能依赖于特定类型的硬件支持（如GPU加速的线性代数库），限制了方法的普适性和在不同硬件平台上的表现。

虽然该论文提出的仿射变换矩阵的优化和量化方法在提升计算和推理效率方面表现出显著优势，同时在保持量化后模型性能上也有良好的表现，但仍需注意数值精度、实现复杂性和硬件依赖性等潜在问题。未来的工作可以探索更多的优化策略和技术，以克服这些挑战，从而在更广泛的应用和硬件环境中部署高效且强大的量化模型。