ICCV2023论文精选！顶会大佬带你深入理解self-attention机制的底层逻辑！¶

论文题目：Understanding Self-attention Mechanism via Dynamical System Perspective

论文链接：https://arxiv.org/abs/2308.09939

摘要¶

自注意力机制（self-attention）广泛应用于人工智能的各个领域，成功地提升了不同模型的性能。然而，目前对这种机制的解释主要基于直觉和经验，而对于自注意力机制如何帮助性能的直接建模仍然缺乏。为了缓解这个问题，在本文中，基于残差神经网络的动力系统视角，我们首先展示了在常微分方程（ODEs）的高精度解中存在的本质刚度现象（SP）也广泛存在于高性能神经网络（NN）中。因此，NN在特征层面上测量SP的能力是获得高性能的必要条件，也是影响NN训练难度的重要因素。类似于在求解刚性ODEs时有效的自适应步长方法，我们展示了自注意力机制也是一种刚度感知的步长适配器，它可以通过细化刚度信息的估计和生成自适应的注意力值，增强模型测量内在SP的表征能力，从而提供了一个关于为什么和如何自注意力机制可以提高模型性能的新理解。这种新的视角也可以解释自注意力机制中的彩票假设，设计新的表征能力的定量指标，并启发了一种新的理论启发式方法，StepNet。在几个流行的基准数据集上的大量实验表明，StepNet可以提取细粒度的刚度信息并准确地测量SP，从而在各种视觉任务中取得显著的改进。

1. 创新点¶

本文的贡献总结如下:

1. 我们提出了一种对自注意力机制的新理解，并揭示了自注意力机制和刚性ODEs数值解之间的紧密联系，这是理解自注意力机制如何提高NN性能的有效解释。
2. 基于我们对自注意力机制的新视角，我们解释了自注意力机制中的彩票假设，设计了新的表征能力的定量指标，并提出了一种强大的理论启发式方法，StepNet。

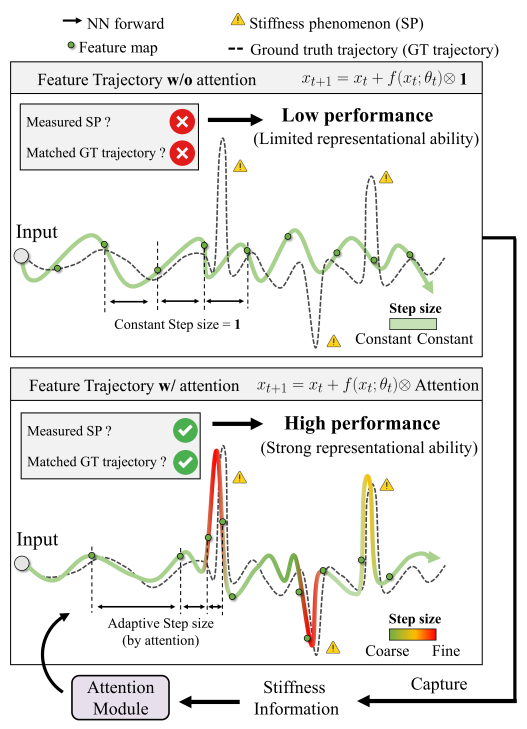
图1. 有无注意力机制的特征轨迹对比。最佳性能模型生成的GT轨迹反映了刚性现象的本质特征。自注意力机制作为一种刚度感知的步长自适应器，能够有效地提取刚度信息，并利用其强大的表示能力来逼近GT轨迹中的刚性现象，从而提高了模型的性能。

2. 刚性现象和自注意力机制¶

在本节中，我们首先介绍刚性ODEs、自注意力机制和具有残差块的NN的动力系统视角的概念。然后我们进一步探索NN中的SP，并将其与自注意力机制联系起来，这最终激发我们提出一种理论启发式方法。

2.1 预备知识和相关工作¶

2.1.1 神经网络的动力系统视角¶

有许多著名的网络结构具有残差块，如ResNet， UNet， Transformer， ResNeXt等。同一阶段的残差块可以写成

其中$x_t\in \mathbb{R}_d$是神经网络$f(\cdot;\theta_t)$的第$t$个块的输入，$\theta_t$是第$t$个块中的可学习参数。许多最近的工作建立了残差块和动力系统之间的深刻联系，揭示了残差块可以被解释为数值方法的前向过程，即$u_{t+1}=u_t+S(u_t;f,\Delta t)\cdot\Delta t$，对于一个ODEs的数值解如下

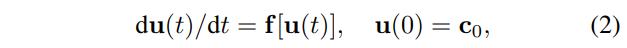
其中$c^0$表示一个初始条件，对应于残差网络的输入。$u(t)\equiv u_t$是一个时间相关的$d$维状态，用于描述第$t$个块中的输入特征$x_t$。神经网络第$t$个块中的输出$f(\cdot;\theta_t)$可以看作是使用数值方法$S$的步长$\Delta t$进行积分$S(u_t;f，\Delta t)$。例如，前向欧拉方法。

2.1.2 ODEs中的刚性¶

在数学上，刚性方程是指数值方法在求解该方程时数值不稳定的微分方程，导致预测效果差。对于大多数ODEs，刚性是普遍存在的和内在的。当解不稳定时，我们可以使用比粗略步长$\Delta t$更细的步长来获得更细致的微分，从而进行高精度积分。因此，利用基于特定数值方法的自适应步长是解决刚性ODEs最直接的方式，如从第四阶Runge-Kutta方法到Runge-Kutta-Fehlberg方法的改进。然而，并没有一个被广泛接受的刚性的数学定义，但其主要思想是该方程包含一些项，这些项会导致解的快速变化。

因此，为了在一定程度上量化刚性，提出了一些简化的指数，如通用刚性指数(SI)$\zeta_{SI}$和刚性感知指数(SAI)$\zeta_{SAI}$。具体来说，对于状态方程(2)中的状态动力学$u(t)$，在$u_t$处的SI定义为$\zeta_{SI}(u_t)=\max(|Re(\lambda_i)|)$，其中$\lambda_i$ 是在 $u_t$处右端方程(2)雅可比矩阵的特征值。雅可比矩阵的最大特征值(实部)表示解的变化速度。一些数据驱动的设置中，方程(2)右端的解析表达式$f$未知。在这种情况下，考虑SAI，因为SAI不需要已知$f$，并且SAI可以看作是SI的代理。对于从给定系统观测到的数据$\{u^{t_i}\}^{N-1}_{i=1}$，在$u_{t_i}$处的SAI可以定义为

从公式(3)可以看出，有限差值$\frac{u^{t_{i+1}}-u^{t_i}}{t^{i+1}-t_i}$的范数可以近似未知函数$f$在$u_{t_i}$处的瞬时变化。术语$1/\|u_{t_i}\|^2$用于消除$\{u_{t_i}\}^{N-1}_{i=1}$不同坐标系中的幅值偏差。如果我们只想测量刚度的相对信息，例如刚度的等级，我们可以使用一个简化的SAI，即 $\tilde{\zeta}_{SAI}(u_{t_i})=\frac{u_{t_{i+1}}-u_{t_i}}{t_{i+1}-t_i}$，作为一种新的刚度信息测量进行分析。

2.2 测量神经网络中的刚性现象¶

在本节中，基于ODEs中刚性的定义以及第2.1节中提出的残差块的动力系统视图，我们从两个方面定义神经网络特征轨迹$\{x_1，x_2，...\}$在公式(1)中生成的刚性现象。首先，(1)从局部角度出发，我们使用公式(3)的思想和定义1提出神经刚性指数(NSI)，使用相邻特征的变化来度量刚性现象。NSI可用于直观地定性可视化刚性现象。但是，根据关于刚性ODEs的相关工作，NSI需要大于某个阈值，即局部变化需要足够大，才被认为发生了刚性现象。然而，不同场景中的阈值各不相同，很难确定一个统一的阈值。

因此，第二，(2)从全局角度出发，我们提出一个称为总神经刚性(TNS)的通用指标，使用NSI对给定数据集上的任何神经网络的刚性现象进行定量测量。公式(5)中定义的TNS考虑了所有阈值设置，包括相对阈值$\mu(1+M_1)$和绝对阈值$M_2$，$M\in\mathbb{R}^{+\times\mathbb{R}}+ $。TNS值越大，表示在特征轨迹上刚性现象越明显。定理1保证了TNS的收敛性。此外，从公式(4)可知，计算NSI需要特征的2范数。然而，前面的工作表明，每个阶段的第一块中的范数通常非常大且敏感，这可能会影响公式(5)的计算。因此，我们在测量TNS时会排除这些特征。

定义1.(神经刚性指数)对于由具有L个残差块的神经网络生成的特征轨迹$x_1，x_2，...，x_L$，即$x_{t+1}=x_t+f(x_t;\theta_t)\cdot\Delta t$，$t=0，1，...，L-1$。在$x_t$处的神经刚性指数为

例如，对于公式(1)中的NN，$\zeta_{NSI}(x_t)=\frac{\|x_{t+1}-x_t\|_2}{\|x_t\|_2}$。

定义2.(总神经刚性)在定义1中，当存在$t$，满足$\zeta_{NSI}(x_t)\geq\max(\mu(1+M_1)，M_2)$时，特征轨迹具有度量为$M=(M_1，M_2)$的刚性$\zeta_{NSI}(x_t;M)$，其中$\mu$是$x_t$所有特征NSI的均值。对于从测试分布$P(x_0)$中采样的输入$x_0$，总神经刚性为$\int_{M}\delta(M)dM$，其中

$I$是特征函数，即当$\zeta_{NSI}(x_t)$不小于$\max(\mu(1+M_1)，M_2)$时，$I=1$，否则$I=0$，$M\in\mathbb{R}^{+\times\mathbb{R}}+ $。

定理1. 对于如公式(5)定义的$\delta(M)$，总神经刚性$\int_{M}\delta(M)dM$收敛。

2.3 真实轨迹¶

为了探索刚性现象在神经网络中的属性，希望有一个“真实轨迹”，以便我们可以分析刚性现象属性与模型性能之间的关系，从而为模型提出具体的改进。给定数据集$D(x，y)$和具有残差块的网络$A(\theta_0，s)$，其中$\theta_0$是初始化参数，$s$表示训练设置(例如，学习率，权重衰减等)。我们将定义3中的某些特征轨迹，其对应模型$A(\theta_0，s)$具有极大性能，视为真实轨迹。

定义3.(真实轨迹)对于数据集$D(x，y)$，任务导向性能指标$\kappa$和具有初始化参数$\theta_0$及训练设置$s$的残差神经网络$A(\theta_0，s)$。在训练后，对于给定的输入$x_0$到相应的输出$y_0$，存在无限多个特征轨迹$[x_{i1}，x_{i2}，...]，i=1，2，...，\infty$。真实轨迹是那些$A(\theta_0，s)$在$D(x，y)$上的性能可以达到的特征轨迹。

首先，定义3中的真实轨迹。考虑非空集合$K$，其元素是在所有初始化参数$\theta_0$和训练设置$s$下的指标$\kappa$。注意，任务导向性能指标$\kappa$在各种深度学习任务中通常是有界的，特别是在有监督学习中，例如，分类任务的指标的上界是100\%，所以$\kappa(A(\theta_0，s)，D(x，y))<+\infty$。每个非空子集$\subset\mathbb{R}$只要有上确界就有上确界，因此集合$K$有上确界，这意味着真实轨迹存在。

图2. 通过TNS对不同残差块模型在CIFAR100和STL10数据集上的刚性现象的定量可视化。

然而，对于给定的输入$x_0$及其相应输出$y_0$，这种轨迹可能不是唯一的，这将在附录中予以说明。此外，如上所述，特征轨迹是数据驱动的，且神经网络中右端方程(2)的解析表达式未知。因此，不可行获得真实轨迹的解析形式，取而代之的是，某些高级自注意力网络的轨迹，如SENet，可以作为真实轨迹的代理来经验地逼近真实轨迹的属性。因此，我们以ResNet164为骨干，选择四个高性能自注意力网络，即SENet， FCANet， ECANet和SRMNet，来逼近分析真实轨迹的属性。在图2中，我们展示了每个网络在不同$M_1，M_2$下的TNS。对于CIFAR100和STL10数据集，从图2中的所有高性能网络的结果中，我们观察到真实轨迹具有显著较大的TNS。换句话说，对于大多数输入，真实轨迹具有刚性现象。尽管原始残差神经网络的TNS相对较小，但它仍然可以在一定程度上测量刚性现象。

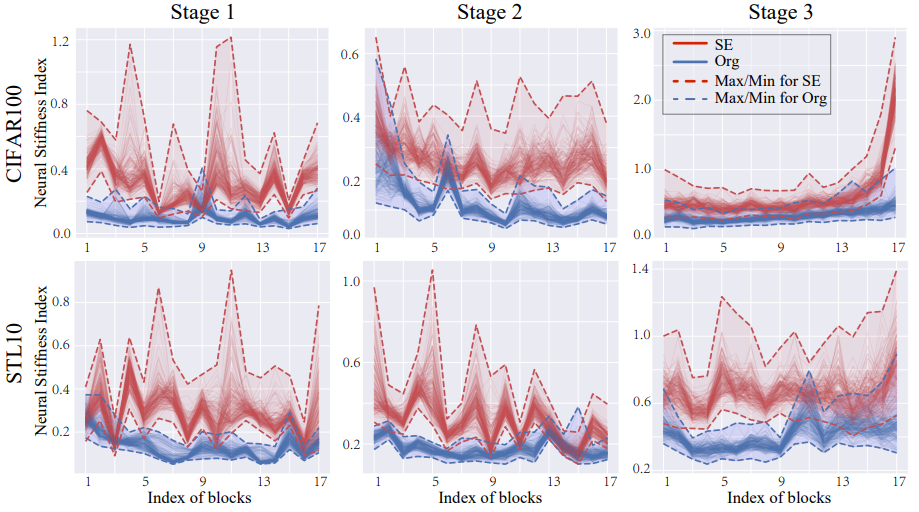
图3. 通过NSI直观可视化SENet164和ResNet164在CIFAR100和STL10数据集上的刚性现象。

此外，由于我们可以经验地观察到这些高性能网络中普遍存在刚性现象，我们推测刚性现象的存在是真实轨迹的内在属性（更多讨论见第3.1节）。因此，如果一个神经网络结构可以更好地估计刚度信息以测量和捕获刚性现象，例如，具有高TNS，那么这样的结构可以生成更接近真实轨迹的特征轨迹，从而取得高性能。反之，如果一个神经网络结构本质上不能测量刚度信息，它可能会在其特征轨迹与真实轨迹之间产生较大偏差。这样的偏差将随着神经网络的正向过程逐渐累积，导致预测性能差。最后，在图3中，我们使用定义1的NSI提供了刚性现象的直观可视化。显然，在CIFAR100和STL10数据集上，我们可以观察到用SENet测量的真实轨迹在每个阶段都有明显和急剧的震荡，表现出刚性现象。“Org”测量的轨迹相对平滑，但也有一些与图2中的观察一致的震荡。

2.4 自注意力机制¶

在本节中，我们引入自注意力机制，并基于前面部分介绍的神经网络的动力系统视角，揭示它在提高模型性能方面发挥的作用。为了文章中的分析，我们以通道注意力神经网络为例。对于通道自注意力网络，它们可以通过与公式(1)比较来表示：

其中$\otimes$是哈达马积，F($\cdot$;$\phi_t$)是第$t$个块中基于不同注意力方法的自注意力模块，具有可学习参数$\phi_t$。例如，在SENet中，F($\cdot$;$\phi_t$)=$W^{t1}$(ReLU($W^{t2}(\cdot)$))，其中$W^{t1}\in\mathbb{R}^{d\times r}$和$W^{t2}\in\mathbb{R}^{r\times d}$是可学习矩阵，$r<d$。

与第2.1.2节中提到的前向数值方法相比，公式(7)中的注意力值F($f(x_t;\theta_t);\phi_t$)可以看作是求解ODE的步长$\Delta t$，原始的残差神经网络可以重写为

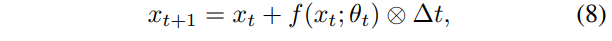
其中步长$\Delta t=1$。通过比较公式(7)和公式(8)，我们可以容易地发现自注意力机制生成的注意力值确实充当自适应步长，即$\Delta t$=F($f(x_t;\theta_t);\phi_t$)。此外，由于各种自注意力模块的最后一层通常是Sigmoid函数或Softmax函数，因此公式(7)中的注意力值小于1，即$\Delta t=$F($f(x_t;\theta_t);\phi_t$)<1。这意味着使用自注意力机制，我们可以提供比原始残差神经网络更小、更灵活的步长。

现在我们展示自注意力机制生成的步长也是刚度感知的。如第2.1.2节所述，我们可以使用($\frac{x_{t+1}-x_t}{\Delta t}$)来测量特征轨迹在$x_t$处的刚度信息。那么对于原始残差神经网络公式(1)，我们有

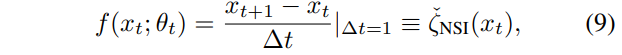
因此$f(x_t;\theta_t)$可以看作是一种粗略的刚度信息，其中步长$\Delta t$=1，这与第2.3节中图2和图3的讨论是一致的。对于自注意力机制，我们有

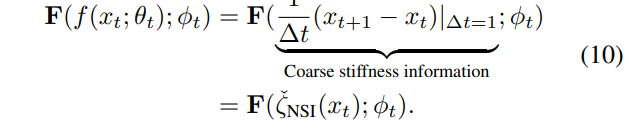
从公式(10)中，我们可以总结自注意力模块如何帮助原始残差神经网络的性能:

(1)捕获刚度信息。自注意力模块F($·;\phi_t$)将可访问的和粗略的刚度信息f($x_t;\theta_t$)作为输入，来自公式(9)。然后，如图2和图3所示，自注意力模块可以改进这种粗略信息以获得更精细的刚度信息估计;

(2)生成自适应步长。基于这种更精细的估计，模块F(·;$\phi_t$)输出适当的注意力值$F(f(x_t;\theta_t);\phi_t$)，以自适应地测量神经网络中的刚性现象，这意味着自注意力机制可以增强神经网络的表示能力。例如，如果在特征$x_t$需要测量一个较大的NSI，从公式(4)中可以看出，注意力值$F(f(x_t;\theta_t);\phi_t)$可以较小以获得较大的$\zeta_{NSI}(x_t)=\frac{1}{\|x_t\|^2}\|\frac{\hat{x}^{t+1}-x_t}{F(f(x_t;\theta_t);\phi_t)}\|_2$。

2.5 理论启发的方法:StepNet¶

从第2.4节和公式(10)中，我们知道正确估计刚度信息的能力对自注意力模块的性能至关重要。因此，如果我们想获得更好的模型性能，可以考虑在自注意力模块中估计其他可访问和更好的刚度信息。现在我们引入一个更好的自注意力公式，以捕获更好的刚度信息，这是由SI和SAI之间的渐近分析激发的，如下所示。在第2.1.2节中，SAI被用作ODE中刚性的通用指数(SI)的代理，以度量刚性信息，以解决SI在数据驱动问题中的计算困难。在定理2中，我们首先展示SAI如何逼近SI。

定理2. 对于定义在公式(2)中的ODEs$\frac{du(t)}{dt}=f[u(t)]$，如果在$u_t$处的雅可比矩阵$J_{u_t}$是一个n×n对称实矩阵，且$\{λ_i\}^n_{i=1}$是它的n个不同特征值，且$Re(λ_i)<0$，$i=1，2，...，n$，则

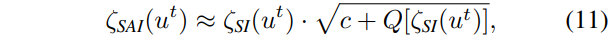
其中c是一个常数，$Q(\cdot)$是一个关于$\zeta_{SI}(u_t)$的函数，当$\zeta_{SI}(u_t)$足够大时，$Q[\zeta_{SI}(u_t)]$收敛于0。

受上面的分析的启发，我们提出了一个新的自注意力网络，称为StepNet。如第2.4节所讨论的，正确估计刚度信息对自注意力模块的性能至关重要。因此，对于公式(10)，我们使用一个数据驱动函数$\tilde{F}(x_{t+1}，x_t;\tilde{\phi}_t)=\tilde{F}(x_t+f(x_t;\theta_t)，x_t;\tilde{\phi}_t)$来替换$F(x_{t+1}-x_t;\phi_t)$，以便自适应步长在我们的StepNet中基于相邻状态$x_{t+1}$和$x_t$之间的内在关系生成，以更好地建模刚度信息。因此，公式(7)可以重写为

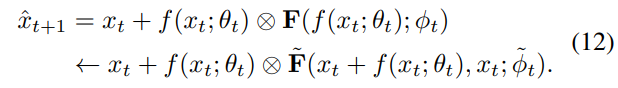
从公式(12)可以看出，我们的StepNet的计算有两个阶段:(1)在图4(a)中，我们首先通过公式(1)估计一个粗略的第(t+1)特征图$x_{t+1}=x_t+f(x_t;\theta_t)$;(2)之后，自适应器 $\tilde{F}(\cdot，\cdot;\tilde{\phi}_t)$以$x_t$和$x_{t+1}$为输入生成自适应注意力值，这可以更好地测量刚度信息以生成更精细的步长，以便更好地捕获刚性现象，从而增强模型的表示能力和性能。自适应器的网络架构如图4(b)所示，更多训练细节提供在附录中。

图4. StepNet的架构。

3. 实验结果与分析¶

在本节中，我们使用几个流行的视觉基准来验证所提出的StepNet的有效性，包括图像分类和目标检测。所有实验已使用随机种子验证5次，报告的是平均性能和标准差。

表1. 在CIFAR10、CIFAR100和STL10上的分类精度。“#P(M)”表示参数量(百万)。最佳和第二佳结果分加粗和加下划线。

表2. 在ImageNet上的分类性能。最佳和第二佳结果分加粗和加下划线。

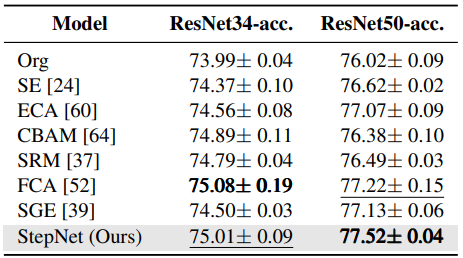
图像分类。我们在四个数据集上比较了所提出的StepNet与几种现有的自注意力模块进行图像分类。这四个数据集是CIFAR10，CIFAR100，STL-10和ImageNet，结果如表1所示，显示StepNet相对于原始网络和其他现有的自注意力模块在不同的数据集和骨干网络下持续提高了准确率。

表3. 在MS COCO上的目标检测性能。最佳和第二佳结果分加粗和加下划线。

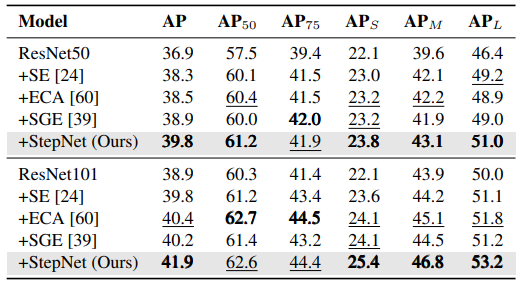
对象检测。我们进一步对MS COCO数据集进行对象检测任务的实验，使用Faster R-CNN，结果如表3所示，StepNet分别在ResNet50和ResNet101上改进了AP 2.9%和3.0%。此外，StepNet在其他目标检测指标上也实现了良好的性能改进。所有结果表明，我们对自注意力机制的新理解可以有效地帮助我们设计自注意力机制。

3.1 激励研究和讨论¶

现在我们进一步探索StepNet的属性和神经网络中的刚性现象。

表4. 对StepNet结构的激励研究。

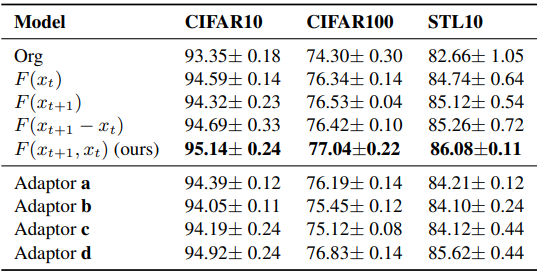
StepNet的结构。在第2.4节中，我们总结自注意力机制可以通过两种方式帮助模型性能，即刚度信息的提取和自适应步长的生成。事实上，这两种方式对应于(1)自注意力模块的输入和(2)模块的设计。对于(1)，在表4中，我们探索了在移除$x_t$或$x_{t+1}$时的性能，结果表明同时具有$x_t$和$x_{t+1}$的输入对估计精细刚度信息是必要的，这与第2.5节中的讨论一致。此外，F($x_{t+1}-x_t$)意味着我们只在StepNet的自适应器中使用正常范式的自注意力模块，不考虑公式(12)中更好的刚度估计。将F($x_{t+1}-x_t$)与我们的F($x_{t+1}，x_t$)进行比较，我们可以看出像我们这样的更精细刚度信息估计是必要的，以取得更好的性能。对于(2)，如图5所示，我们构造了四种替代自适应器结构。实验结果表明，所有四种替代方案均劣于我们的方案。但是，生成自适应步长的最佳结构仍未知，未来我们仍可以改进自适应器的设计，例如，通过神经网络有效利用$x_t$和$x_{t+1}$。

图5. 自适应器的不同结构。

刚性现象的属性和自注意力机制的彩票假设。事实上，对于任意输入$x_0$及其对应的输出$y_0$，经过良好训练的残差神经网络生成的特征轨迹具有两点属性:(1)对于大多数输入$x_0$，其特征轨迹具有刚性现象;(2)对于每个轨迹，只有少量特征可以引起刚性现象。具体来说，对于属性(1)，在第2.3节中，我们用几种高级自注意力模型来逼近真实轨迹。从图2和图3中，我们可以经验地观察到，对于大多数输入，其特征轨迹具有刚性现象。在附录中，我们提供了更多使用SENet作为示例的特征轨迹的可视化，这些可视化也为属性(1)提供了经验证据。对于属性(2)，我们定义刚性比例$\hat{p}= \frac{1}{L} \mathbb{E}_{x_0\sim P(x_0)}\# \{t|\zeta_{NSI}(x_t)\geq\max(\mu(1+M_1)，M_2)\}$来测量特征轨迹中具有度量为M的$\zeta_{NSI}(x_t;M)$的期望特征数量。如果一个特征轨迹的$\hat{p}$接近100\%，则意味着该轨迹有许多特征具有足够大的NSI。对于图4，我们在图6中显示了相应的刚性比例。我们可以观察到，对于各种$M_1$和$M_2$，大多数$\hat{p}\leq10\%$，这表明真实轨迹中只有少数特征可以引起刚性现象。

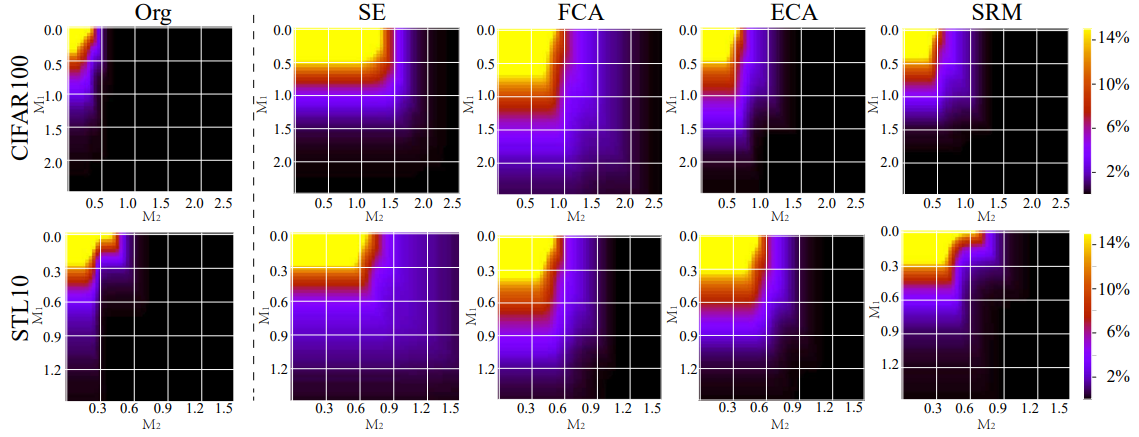
图6. 不同模型在CIFAR100和STL10数据集上刚性比例。

另外，我们发现这两种属性与自注意力机制中的彩票假设密切相关。彩票假设揭示我们只需要在少数块上插入自注意力模块就可以取得显著改进。根据属性(1)，对于大多数输入，它们的真实轨迹有刚性现象，如第2.4节所述，自注意力机制生成的自适应步长可以提高神经网络的表示能力。因此，自注意力机制对于大多数输入都是有效的。此外，属性(2)告诉我们，特征轨迹中只有少量特征可以引起刚性现象，因此我们只需要在少数块上设置模块来测量整个轨迹的刚性现象。因此，如果这两种属性普遍成立，我们认为彩票假设也可能是自注意力机制的一种内在属性。

真实轨迹为何具有刚性现象？现在我们试图理解为什么大多数真实轨迹具有刚性现象，这可以帮助我们设计新的方法来提升表示学习的性能。从公式(4)和公式(9)中，我们知道对于一个训练良好的残差神经网络，f(x_t;\theta_t)提供刚度信息和$\zeta_{NSI}(x_t)=O(\|f(x_t;\theta_t)\|^2)$。当NSI较大时，$\|f(x_t;\theta_t)\|^2$也较大，这意味着神经网络$f(\cdot;\theta_t)$在第$t$个块的输出特征的元素(绝对值)相对较大。在一些前面的工作中，这种特征被认为是重要特征，对模型性能有主要贡献。换句话说，残差网络可能之所以能达到高性能，即它能逼近真实轨迹，是因为网络具有通过自适应步长在少数块中学习这样的重要(刚性)特征的能力。因此，我们进一步计算TNS与模型性能之间的秩相关性(肯德尔相关性和斯皮尔曼相关性 )。图7中的结果表明，模型的性能及其测量刚性现象的表示能力呈正相关。此外，由于TNS可以反映模型测量刚性现象的能力，因此TNS也可以是神经网络实践中评估表示能力的新指标，并有望用于网络构建，如神经体系结构搜索，网络剪枝或其他应用。

图7. 准确率与总神经刚性之间的相关性。

4. 结论¶

在本文中，我们建立了自注意力机制（自注意力机制）和刚性常微分方程数值解之间的关系，揭示了自注意力机制是一种刚度感知的步长适配器，它可以细化刚度信息的估计并生成合适的注意力值，以自适应地测量神经网络（NN）中的刚度现象，从而提高NN的表征能力并获得高性能。