ICLR2024 oral：小尺度Transformer如何Scale Up

ICLR 2024 oral： Small-scale proxies for large-scale Transformer training instabilities¶

1. 论文信息¶

2. 引言¶

这篇论文探讨了在放大Transformer模型时遇到的一系列训练不稳定性问题，并提出了研究和预测这些不稳定性的方法。作者指出，尽管将Transformer模型扩展到更大的规模已经在从聊天模型到图像生成等多个领域取得了显著进展，但并非每一次训练尝试都会成功。在训练大型Transformer模型时，研究人员报告了一些不稳定性，这些不稳定性会减缓或破坏学习过程。

文章通过复现、研究并预测Transformer模型训练中的不稳定性，发现衡量学习率和损失之间的关系是识别不稳定性的有用工具。因此，引入了学习率敏感性(LR sensitivity)作为对学习率与损失曲线的一个有用的总结性统计量。LR敏感性衡量了在学习率变化几个数量级时，与最优性能的偏离程度。

研究表明，两种先前在大规模模型中描述的不稳定性源也可以在小型Transformer中复现，这使得研究者无需大量资源就能研究这些不稳定性。特别是，文章检查了attention 层中logits的增长和输出logits与对数概率的发散，发现这些不稳定性在使用高学习率的小模型中出现。此外，之前在大规模应用中成功的干预措施，在这种情况下也同样有效。

这些干预措施包括qk-layernorm和z-loss正则化，它们可以降低LR敏感性，使得在三个数量级的学习率变化中成功训练成为可能。文章还研究了其他已知的优化器和模型干预措施（如预热、权重衰减和μParam）对学习率与损失曲线形状的影响，发现这些技术通常对于可以稳定训练的学习率范围影响不大，但会影响该范围内的学习率敏感性。

进一步的研究集中在模型特性（如激活和梯度范数）的规模化行为上，展示了在不稳定性出现之前就可以预测它的可能性。文章通过扩展模型特性的规模化行为来寻找当前尚未充分记录的不稳定性，发现梯度范数随着规模和学习率的增加而减少，导致默认的AdamW epsilon超参数过大，从而导致更新过小。这与参数范数增长和attention logit增长不稳定性有关。

总的来说，这项工作为在没有大量资源的情况下研究训练稳定性提供了新的科学机会，展示了对于解决Transformer模型训练中的不稳定性问题，有着重要的理论和实践意义。

3. 方法¶

在这项研究中，实验设定围绕着训练小型Transformer模型，模型训练设定参考了GPT-2的实验架构，并使用Flax框架实现。这些模型是仅包含解码器的，采用自回归损失进行训练。实验中操作了多个超参数，但除非另有说明，否则会使用一系列默认值。

3.1 LR vs. loss curves and learning rate sensitivity¶

这一节主要探讨了在小规模下复现两种已知不稳定性：attention logits增长和输出logits与对数概率的发散，以及如何通过实验方法减轻这些不稳定性。研究通过绘制学习率与损失曲线，展示了在高学习率下使用小型模型时可以复现这些不稳定性，并且大规模应用中有效的缓解措施在此环境下也同样有效。

3.2 LR vs. loss curves and learning rate sensitivity¶

在研究模型训练过程中的不稳定性时，分析模型特性（如梯度或激活范数）的规模化趋势是一个非常有用的方法。这种方法有助于预测潜在的不稳定性，并与之前主要关注模型规模与损失之间趋势的研究形成对比。通过细致观察这些模型内部特性的变化，研究人员可以在问题发生之前识别出可能导致训练不稳定的信号，为制定有效的干预措施提供依据。

梯度范数和激活范数这类模型特性对于理解深度学习模型的训练动态至关重要。梯度范数可以反映模型参数更新的幅度，其规模化趋势可能揭示梯度消失或梯度爆炸等问题，这些都是导致模型训练不稳定的常见原因。同样，激活范数的规模化趋势可以揭示网络层的激活值是否过高或过低，这可能影响网络的学习能力和泛化性能。

4. 实验结果¶

4.1 减少复现过程中small scale的不稳定性¶

这一节主要探讨了在小规模下复现两种已知不稳定性：attention logits增长和输出logits与对数概率的发散，以及如何通过实验方法减轻这些不稳定性。研究通过绘制学习率与损失曲线，展示了在高学习率下使用小型模型时可以复现这些不稳定性，并且大规模应用中有效的缓解措施在此环境下也同样有效。

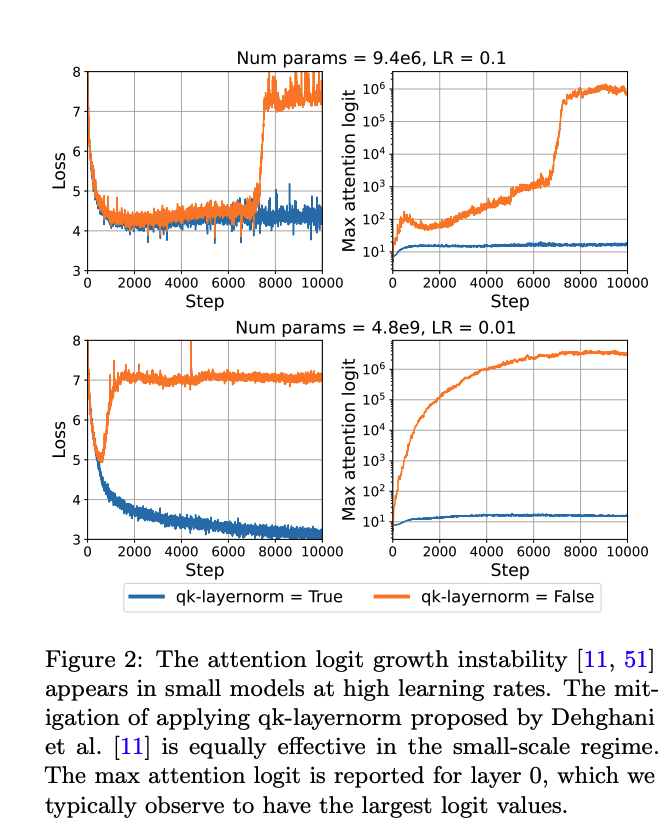
attention logits增长¶

先前的研究表明，当attention logits变大时，Transformer训练会失败。在自attention 层中，通过查询（queries）和键（keys）的组合来计算attention logits，当这些logits变大时，会导致attention 权重倒向one-hot向量，从而导致attention 熵的崩溃。为了解决这一问题，提出了应用qk-layernorm的方法，通过在计算attention logits之前对查询和键进行LayerNorm处理。实验发现，即使是小型模型也会表现出与attention logits增长相关的不稳定性，而使用qk-layernorm可以显著降低LR敏感性，并在高学习率下训练至低损失。

输出logits发散¶

训练大型模型时，另一种报告的不稳定性是输出logits从对数概率中发散。这种情况在模型的输出logits变得非常负时发生，即朝着训练结束时发散。作为缓解措施，提出了鼓励$\log Z$保持接近零的z-loss，通过添加一个辅助损失$\log^2 Z$。实验发现，z-loss能解决与输出logits发散相关的不稳定性，而且权重衰减也能缓解大型模型的这种不稳定性。

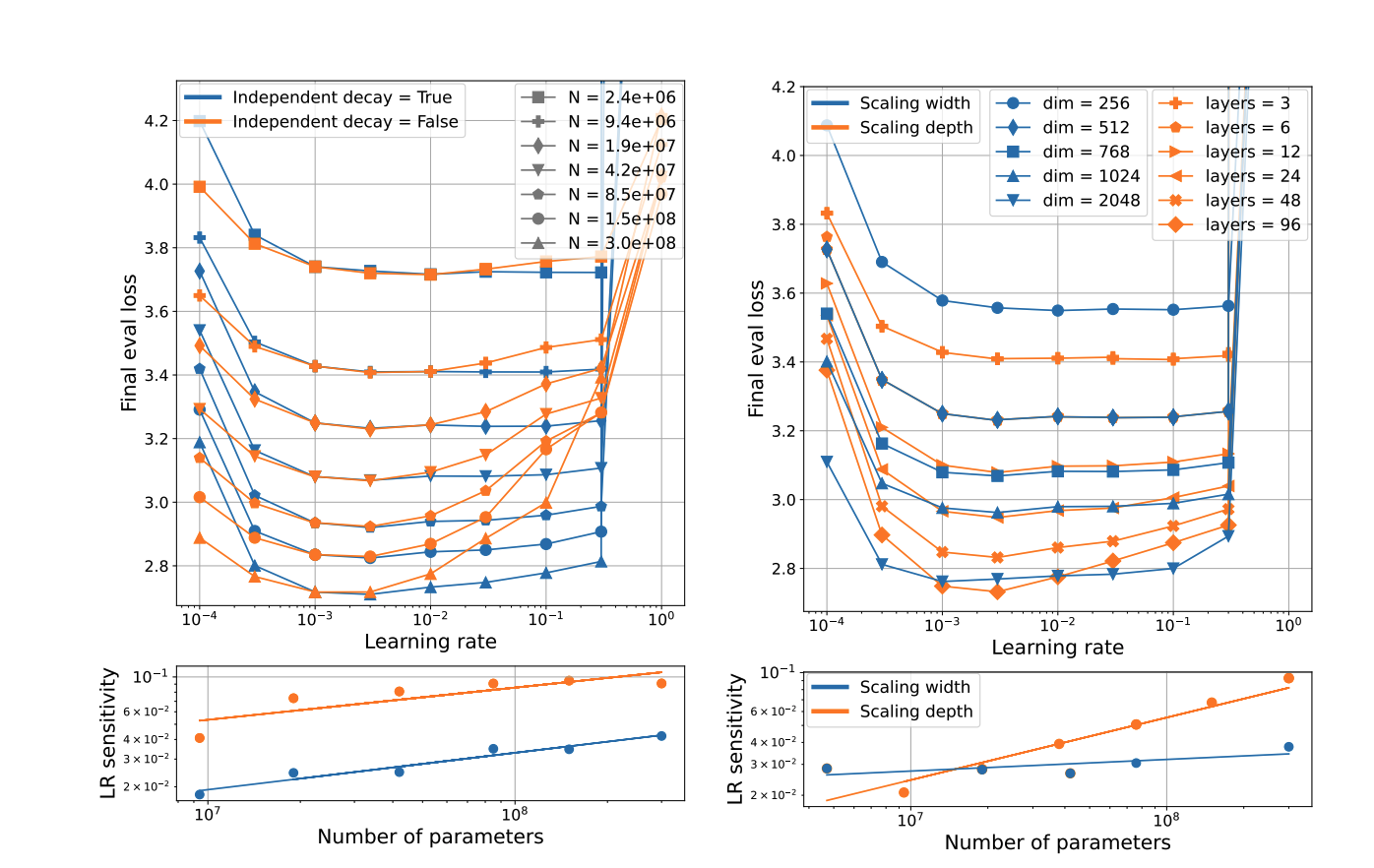
其他干预措施的效果¶

探索了其他已知模型和优化器干预措施对学习率与损失曲线形状的影响，特别是LR敏感性如何帮助识别在规模扩展时的额外问题或解决方案。例如，更长的预热期可以减少LR敏感性，尤其是对于大型模型而言。独立的权重衰减可以减少LR敏感性，而且与学习率独立的参数化权重衰减被证明可以减少LR敏感性。另外，与增加宽度相比，增加深度会更快地提高LR敏感性，但在我们测试的最大规模下，独立增加深度可以产生更低的验证损失。最后，$\mu$Param方法被测试其对LR敏感性的影响，虽然它在我们的实验设置中成功稳定了最优LR，但并未改善损失或减少LR敏感性。

总结来说，这一节详细讨论了通过各种实验干预措施如何在小规模下复现并减轻Transformer模型训练中的已知不稳定性，以及其他干预措施对模型学习率敏感性的影响。

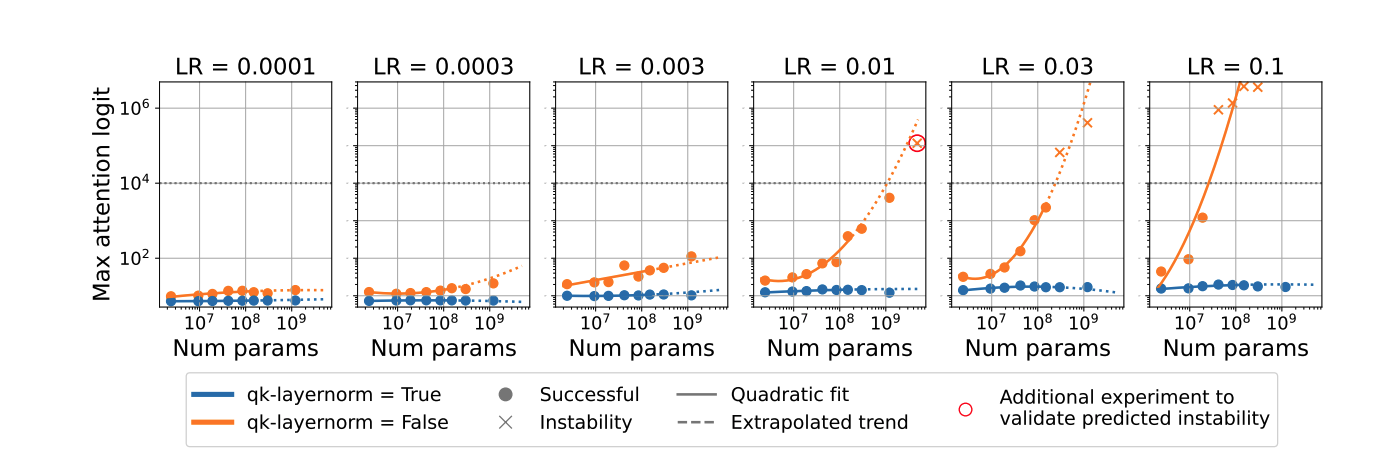
4.2 从模型特征的缩放行为预测attention Logit 增长的不稳定性¶

这一节探讨了如何通过模型特征的规模化行为预测attentionlogits增长不稳定性。通过跟踪不同规模模型的attention logits最大值并拟合曲线，研究者们预测了一个4.8B参数模型在没有qk-layernorm的情况下，学习率为1e-2时会变得不稳定。随后的实验验证了这一预测。

attention logits增长的预测¶

通过对模型参数数量与不同学习率下的最大attention logits进行绘图和二次曲线拟合，发现所有attention logits超过1e4的点都发散了。基于此，预测下一个模型规模在学习率1e-2时的最大attention logits也会超过这一阈值。实验中训练的新4.8B参数模型在该学习率下确实如预测般发散，从而不仅预测了模型的发散，而且准确地外推了最大attention logits的值。

解析不稳定性的起点¶

通过将不同的最大attention logits值植入一个小型网络（10M参数），试图理解不稳定性何时发生，而无需操纵学习率和模型大小。通过调整查询和键的处理函数$g(z) = \sqrt{\kappa} \cdot z/\sqrt{\mathbb{E}_i[z_i^2]}$，实验观察了不同的$\kappa$值对损失的影响。结果显示，当$\kappa$约为1e3时，损失开始恶化，并且当$\kappa$达到1e4时，损失超过了不包含任何自attention 或MLP层的零层bigram模型的损失。

模型特征规模化行为的进一步预测¶

除了attention logits增长外，研究还预测了潜在的不稳定性，通过观察模型特征（如梯度均方根）的规模化行为。发现梯度均方根随模型参数数量和学习率的减小而减小，这表明为了成功扩展模型，可能需要调整超参数，如AdamW的$\epsilon$。如果梯度均方根过小而不调整$\epsilon$或权重衰减，可能会导致层的崩溃。

总结来说，这一节通过模型特征的规模化行为来预测attention logits增长的不稳定性，提供了一种方法论，用于在不稳定性发生前预测并尝试避免这些问题。同时，通过实验探索了不稳定性发生的具体阈值，并对未来模型扩展时可能遇到的其他潜在不稳定性进行了预测和分析。

4.3 通过模型特征的缩放趋势寻找新的不稳定性¶

这一节探讨了如何通过分析模型特性的规模化趋势来预测默认模型和超参数设置可能遇到的新问题。

通过分析梯度的均方根（RMS）随模型规模的变化，发现了一个可能的不稳定性源：随着模型规模的增大，梯度RMS逐渐接近AdamW优化器的默认$\epsilon$超参数值。AdamW优化器未缩放的更新公式为$\Delta = v / (\sqrt{u} + \epsilon)$，其中$v$和$u$分别是梯度的一阶和二阶指数移动平均（EMA）。如果梯度RMS与$\epsilon$的数量级相同，那么$\Delta$的大小会减小，导致参数无法如预期那样接收到学习信号。

为了缓解这个问题，一种显而易见的方法是将AdamW的$\epsilon$超参数从默认的1e-8降低。实验显示，对于一个4.8B参数模型，在学习率0.3下将$\epsilon$降至1e-15能改善损失并缓解梯度RMS的崩溃。相反，将$\epsilon$​增加到1e-6会导致不稳定性。

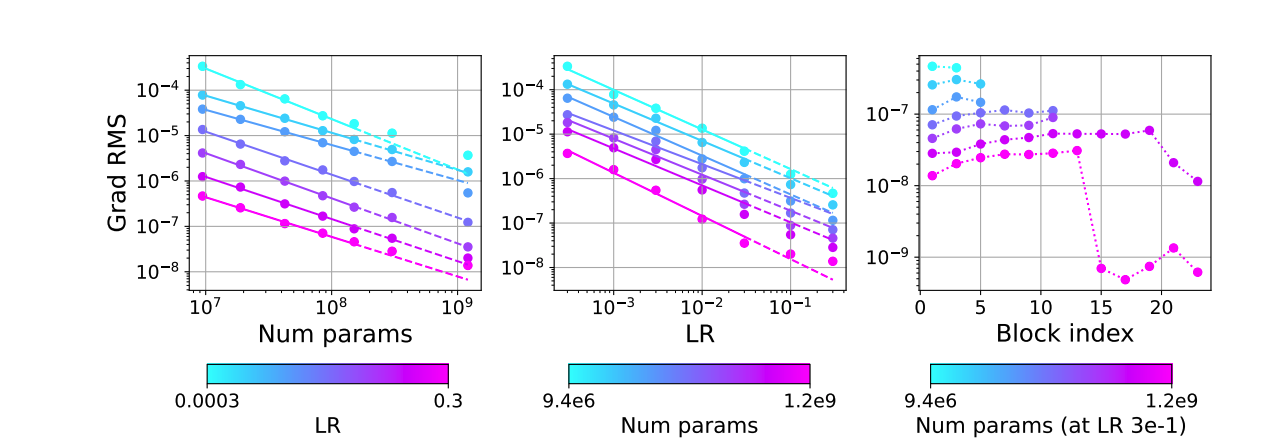
此外，还展示了在我们测试的最大规模和学习率下，整个训练过程中梯度和更新RMS的变化。当梯度RMS达到$\epsilon$值时，更新RMS变得很小。这个问题在我们测试的较大模型和学习率中最为明显。

尽管通过实验测量梯度的规模化行为来识别上述不稳定性，但存在一个机械性解释：对于更大的网络和学习率，Transformer输出进入最终layernorm的RMS可能会增长。因为layernorm的梯度是通过其输入RMS的逆比例缩放的，所以Transformer将接收到较小的梯度。

总之，这一节通过分析模型特性的规模化趋势，预测了可能出现的新问题，并通过调整AdamW的$\epsilon$超参数来进行实验验证和缓解，揭示了在模型规模扩大时需要注意的潜在不稳定性因素。

5. 因素概括¶

这篇论文通过一系列实验，深入探讨了Transformer模型在小规模到大规模训练过程中的稳定性问题，并提出了有效的解决方案。总结其实验验证的结论，可以概括如下几点，以及如何实现从小规模到大规模的成功重现：

1. 注意力logits增长和输出logits发散的不稳定性：通过在小规模模型上复现并验证了大规模模型中已知的两种不稳定性——注意力logits增长和输出logits发散，证明了这些不稳定性也存在于小规模模型中，并且在高学习率下尤为明显。

2. qk-layernorm和z-loss缓解方案的有效性：实验证明，无论是在小规模还是大规模模型中，应用qk-layernorm和z-loss等缓解措施都能有效降低学习率敏感性，提高模型的稳定性和训练效果。

3. 其他干预措施的影响：除了qk-layernorm和z-loss外，论文还探讨了预热、权重衰减、$\mu$Param等其他干预措施对学习率敏感性的影响，发现这些技术通常对可以稳定训练的学习率范围影响不大，但会影响该范围内的学习率敏感性。

4. 通过模型特性的规模化趋势预测不稳定性：论文展示了如何通过分析模型特性（如梯度RMS）的规模化行为来预测潜在的不稳定性问题，并通过实验验证了这些预测。特别是，通过调整AdamW优化器的$\epsilon$超参数，成功缓解了梯度RMS过小导致的学习信号丢失问题。

实现从小规模到大规模的成功重现的关键步骤包括：

• 在小规模模型上识别和解决不稳定性问题：通过在小规模上复现大规模训练中遇到的问题，使用qk-layernorm、z-loss等缓解策略，验证其有效性。

• 分析模型特性的规模化趋势：密切关注模型特性（如梯度RMS）如何随模型规模和学习率变化，利用这些信息预测和防范潜在的不稳定性。

• 调整优化器和超参数设置：根据预测的不稳定性和模型特性的规模化趋势，适当调整优化器参数（如$\epsilon$值）和其他超参数，确保模型在不同规模下的稳定性和性能。

• 持续实验和验证：在模型规模逐步扩大的过程中，持续进行实验和验证，确保缓解措施在不同规模下仍然有效，及时调整策略以应对新出现的问题。

通过遵循这些步骤，研究人员可以更有效地从小规模模型向大规模模型扩展，同时确保训练过程的稳定性和模型性能的优化。

6. 结论¶

这篇论文通过深入研究和实验验证，展示了在小规模和大规模训练Transformer模型时遇到的不稳定性问题，并提出了有效的解决策略。通过分析学习率与损失之间的关系、模型特性的规模化行为，以及不同干预措施的效果，研究团队不仅复现了已知的不稳定性现象，还预测并识别了新的潜在不稳定性，从而为模型训练的稳定性提供了新的科学依据和技术路径。

研究发现，应用qk-layernorm和z-loss等策略可以显著降低学习率敏感性，提高小规模和大规模模型的训练稳定性。此外，通过细致的实验设计，论文验证了其他干预措施如预热、权重衰减、$\mu$Param对于调整学习率敏感性的作用，指出了在模型扩展过程中需要注意的关键因素。

最重要的是，通过对模型特性（如梯度RMS）的规模化趋势分析，研究揭示了可以通过调整优化器参数（如AdamW的$\epsilon$值）来预防和缓解潜在的不稳定性问题。这一发现为进一步扩大模型规模提供了重要的实践指导，有助于推动Transformer模型在各种应用领域中的进一步发展和优化。

本文的工作不仅为理解和解决Transformer训练过程中的不稳定性提供了宝贵的见解和工具，也为未来在资源受限环境下研究大规模模型训练的稳定性开辟了新的道路。通过提出的方法和策略，研究人员可以更加自信地进行模型扩展，优化训练过程，提高模型性能。