前言¶
LSTM模型是基于RNN循环网络提出的一种改进的门控网络 通过各个门很好地控制了时间步前后的信息
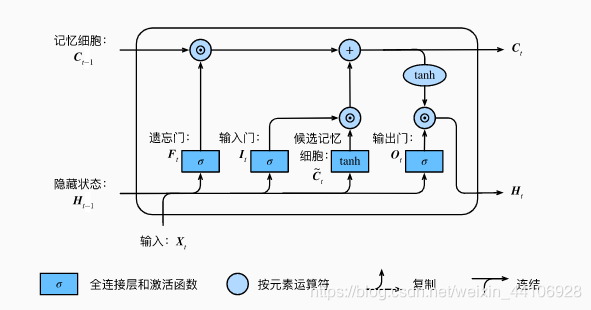
他一共有四个门,分别是遗忘门,输入门,候选记忆细胞,输出门 他能较好地建模长语义,缓解梯度消失的问题
问题提出¶
可以看到我们的输入x和隐藏状态H是==相互独立的==,理论上来说,当前输入应该是和前一时间步的隐藏状态有关,但是LSTM中只是将这两个进行运算,获得各个门的输出。
因此有研究者提出在进入各个门之前,输入和隐藏状态需要做一定的交互运算,而事实证明,这个简单的小改动,大大提升了LSTM的性能
这篇工作也被整理发布,叫Mogrifier LSTM 有兴趣的朋友可以去读一读 https://arxiv.org/pdf/1909.01792.pdf
整体结构¶
作者的这一思想朴素简单,就是在进入门之前对输入和隐藏状态做一定的张量运算


他定义了一个迭代轮数i,当i为奇数的时候执行第一个公式的运算,当i为偶数的时候执行第二个公式的运算。迭代完成后,就进入到传统的LSTM运算当中
这个迭代轮数在实验中是作为一个==超参数==,研究者可以根据任务不同自行调节
我这里也简单地画了一个图
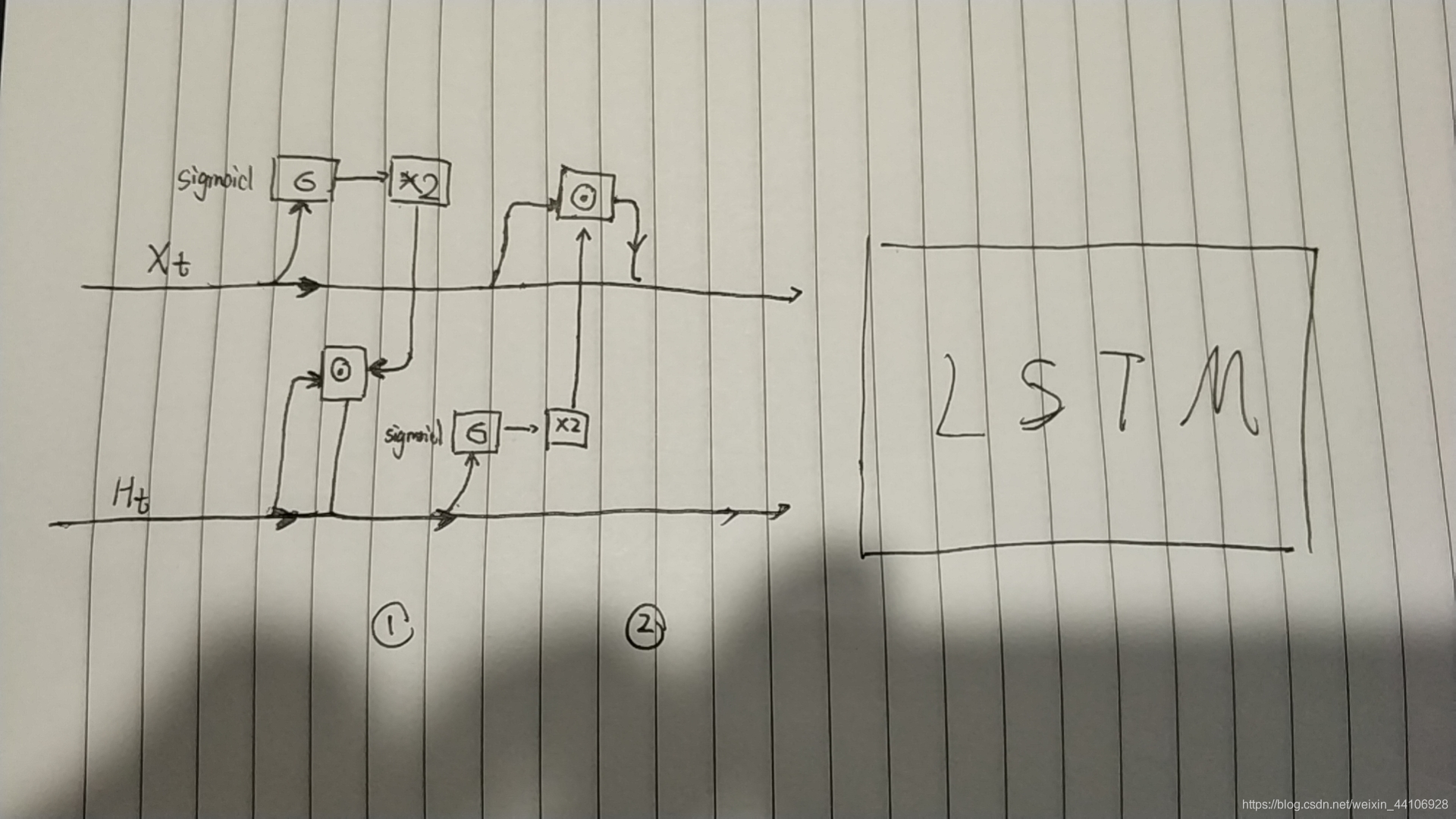
代码实现¶
作者将这个工作整理成了一个jupyter notebook发布在了github上 https://github.com/RMichaelSwan/MogrifierLSTM/blob/master/MogrifierLSTM.ipynb
下面是我对代码做的一些注释
"""
https://github.com/RMichaelSwan/MogrifierLSTM/blob/master/MogrifierLSTM.ipynb
pytorch实现MogrifierLSTM
"""
import numpy as np
import torch
import torch.nn as nn
from torch.nn import Parameter
import torch.optim as optim
from typing import *
from pathlib import Path
from enum import IntEnum
DATA_ROOT = Path("../data/brown")
N_EPOCHS = 210
class Dim(IntEnum):
batch = 0
seq = 1
feature = 2
class NaiveLSTM(nn.Module):
"""
原始LSTM模型
要注意的是在forward里面它把hidden隐藏状态x输入,给concat到一起
所以在初始化的时候,权重这里的输入维度都是inputsz + hiddensz
"""
def __init__(self, input_sz: int, hidden_sz: int):
super().__init__()
self.input_size = input_sz
self.hidden_size = hidden_sz
# Define/initialize all tensors
# forget gate
self.Wf = Parameter(torch.Tensor(input_sz + hidden_sz, hidden_sz))
self.bf = Parameter(torch.Tensor(hidden_sz))
# input gate
self.Wi = Parameter(torch.Tensor(input_sz + hidden_sz, hidden_sz))
self.bi = Parameter(torch.Tensor(hidden_sz))
# Candidate memory cell
self.Wc = Parameter(torch.Tensor(input_sz + hidden_sz, hidden_sz))
self.bc = Parameter(torch.Tensor(hidden_sz))
# output gate
self.Wo = Parameter(torch.Tensor(input_sz + hidden_sz, hidden_sz))
self.bo = Parameter(torch.Tensor(hidden_sz))
self.init_weights()
def init_weights(self):
for p in self.parameters():
if p.data.ndimension() >= 2:
nn.init.xavier_uniform_(p.data)
else:
nn.init.zeros_(p.data)
# Define forward pass through all LSTM cells across all timesteps.
# By using PyTorch functions, we get backpropagation for free.
def forward(self, x: torch.Tensor,
init_states: Optional[Tuple[torch.Tensor, torch.Tensor]] = None
) -> Tuple[torch.Tensor, Tuple[torch.Tensor, torch.Tensor]]:
"""Assumes x is of shape (batch, sequence, feature)"""
batch_sz, seq_sz, _ = x.size()
hidden_seq = []
# ht and Ct start as the previous states and end as the output states in each loop bellow
if init_states is None:
ht = torch.zeros((batch_sz, self.hidden_size)).to(x.device)
Ct = torch.zeros((batch_sz, self.hidden_size)).to(x.device)
else:
ht, Ct = init_states
for t in range(seq_sz): # iterate over the time steps
xt = x[:, t, :]
hx_concat = torch.cat((ht, xt), dim=1)
### The LSTM Cell!
ft = torch.sigmoid(hx_concat @ self.Wf + self.bf)
it = torch.sigmoid(hx_concat @ self.Wi + self.bi)
Ct_candidate = torch.tanh(hx_concat @ self.Wc + self.bc)
ot = torch.sigmoid(hx_concat @ self.Wo + self.bo)
# outputs
Ct = ft * Ct + it * Ct_candidate
ht = ot * torch.tanh(Ct)
###
hidden_seq.append(ht.unsqueeze(Dim.batch))
hidden_seq = torch.cat(hidden_seq, dim=Dim.batch)
# reshape from shape (sequence, batch, feature) to (batch, sequence, feature)
hidden_seq = hidden_seq.transpose(Dim.batch, Dim.seq).contiguous()
return hidden_seq, (ht, Ct)
class MogLSTM(nn.Module):
def __init__(self, input_sz, hidden_sz, mog_iteration):
super(MogLSTM, self).__init__()
self.input_size = input_sz
self.hidden_size = hidden_sz
self.mog_iterations = mog_iteration
# 这里hiddensz乘4,是将四个门的张量运算都合并到一个矩阵当中,后续再通过张量分块给每个门
self.Wih = Parameter(torch.Tensor(input_sz, hidden_sz*4))
self.Whh = Parameter(torch.Tensor(hidden_sz, hidden_sz*4))
self.bih = Parameter(torch.Tensor(hidden_sz*4))
self.bhh = Parameter(torch.Tensor(hidden_sz*4))
# Mogrifiers
self.Q = Parameter(torch.Tensor(hidden_sz, input_sz))
self.R = Parameter(torch.Tensor(input_sz, hidden_sz))
self.init_weights()
def init_weights(self):
"""
权重初始化,对于W,Q,R使用xavier
对于偏置b则使用0初始化
:return:
"""
for p in self.parameters():
if p.data.ndimension() >= 2:
nn.init.xavier_uniform_(p.data)
else:
nn.init.zeros_(p.data)
def mogrify(self, xt, ht):
"""
计算mogrify
:param xt:
:param ht:
:return:
"""
for i in range(1, self.mog_iterations+1):
if(i % 2 == 0):
ht = (2*torch.sigmoid(xt @ self.R)*ht)
else:
xt = (2*torch.sigmoid(ht @ self.Q)*xt)
return xt, ht
def forward(self, x:torch.Tensor, init_states:Optional[Tuple[torch.Tensor, torch.Tensor]]=None) -> \
Tuple[torch.Tensor, Tuple[torch.Tensor, torch.Tensor]]:
batch_sz, seq_sz, _ = x.size()
hidden_seq = []
if init_states is None:
ht = torch.zeros((batch_sz, self.hidden_size)).to(x.device)
Ct = torch.zeros((batch_sz, self.hidden_size)).to(x.device)
else:
ht, Ct = init_states
for t in range(seq_sz):
xt = x[:, t, :]
xt, ht = self.mogrify(xt, ht)
gates = (xt @ self.Wih + self.bih) + (ht @ self.Whh + self.bhh)
ingate, forgetgate, cellgate, outgate = gates.chunk(4, 1) # chunk方法将tensor分块
# LSTM
ft = torch.sigmoid(forgetgate)
it = torch.sigmoid(ingate)
Ct_candidate = torch.tanh(cellgate)
ot = torch.sigmoid(outgate)
# outputs
Ct = (ft*Ct) + (it*Ct_candidate)
ht = ot * torch.tanh(Ct)
hidden_seq.append(ht.unsqueeze(Dim.batch)) # unsqueeze是给指定位置加上维数为1的维度
hidden_seq = torch.cat(hidden_seq, dim=Dim.batch)
hidden_seq = hidden_seq.transpose(Dim.batch, Dim.seq).contiguous()
return hidden_seq, (ht, Ct)
# sanity testing
# note that our hidden_sz is also our defined output size for each LSTM cell.
batch_sz, seq_len, feat_sz, hidden_sz = 5, 10, 32, 16
arr = torch.randn(batch_sz, seq_len, feat_sz)
lstm = MogLSTM(feat_sz, hidden_sz, 2)
ht, (hn, cn) = lstm(arr)
print(ht.shape) # shape should be batch_sz x seq_len x hidden_sz = 5x10x16
总结¶
作者在最后实验当中,也证明了改进后的LSTM在处理相对时间步较长的数据时候,比传统LSTM性能更好。总的来说这个思想简单,效果很好,实验也很充分,是一个不错的工作
本文总阅读量次