IPMI 2023：Test Time Adaptation 的医学图像分割解决

目录¶

• 前言
• 概述
• 具体实现
• 实验
• 总结
• 参考

前言¶

这次我们要解读的工作发表在 IPMI 2023（IPMI全名 Information Processing in Medical Imaging，两年一届，是医学影像分析处理领域公认的最具特色的会议），同时也是 Test Time Adaptation 系列的文章，之前的 TTA 论文解决在：

• CoTTA
• EcoTTA
• DIGA

对 TTA 不了解的同学可以先看上面这几篇新工作。基于深度学习的医学成像解决方案的一个主要问题是，当一个模型在不同于其训练的数据分布上进行测试时，性能下降。将源模型适应于测试时的目标数据分布是解决数据移位问题的一种有效的解决方案。以前的方法通过使用熵最小化或正则化等技术将模型适应于目标分布来解决这个问题。

在这些方法中，模型仍然通过使用完整测试数据分布的无监督损失反向传播更新。但是在现实世界的临床环境中，实时将模型适应于新的测试图像更有意义，并且需要避免在推理过程中由于隐私问题和部署时缺乏计算资源的情况。TTA 在遇到来自未知领域的图像时，有望提高深度学习模型的鲁棒性。本文要介绍的工作属于 Fully Test Time Adaptation，既在推理时需要网络要做完整的反向传播。下表简单列出几种常见 settings，其中 Fully TTA 只需要 target data 和 test loss。

现有的 TTA 方法性能较差，原因在于未标记的目标域图像提供的监督信号不足，或者受到源域中预训练策略和网络结构的特定要求的限制。这篇工作目标是将源域中的预训练与目标域中的适应分开，以实现高性能且更具一般性的 TTA，而不对预训练策略做出假设。

概述¶

这篇工作（被叫做 UPL-TTA）提出了一种用于医学图像分割的 “Uncertainty-aware Pseudo Label guided Fully Test Time Adaptation" 方法，该方法不要求预训练模型在适应到目标领域之前在源域中进行额外的辅助分支训练或采用特定策略。

如下图所示，以婴儿脑部 MRI 肿瘤分割为例，从 HASTE 跨域到 TrueFISP，UPL-TTA 的效果要比不做任何适应的结果好很多。

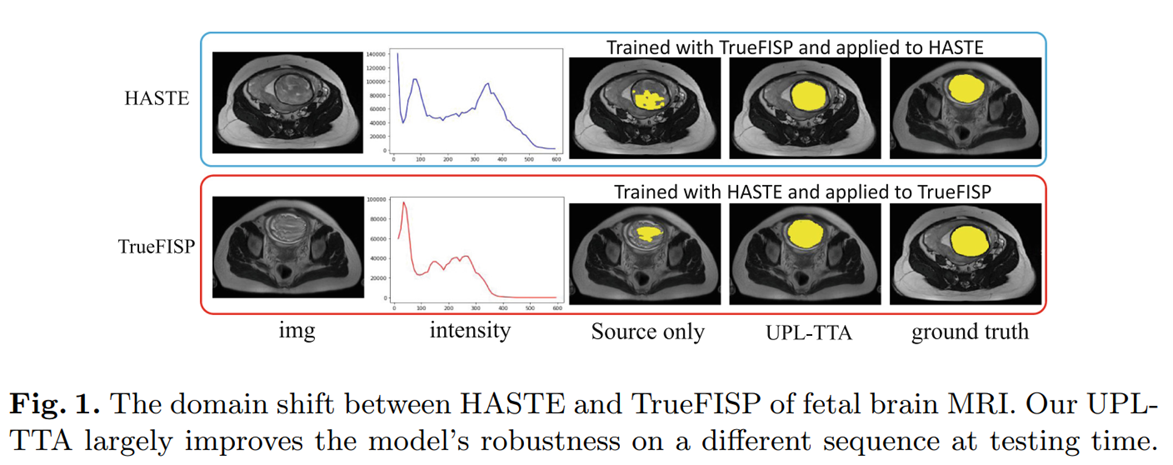
UPL-TTA 首先引入了 Test Time Growing（TTG），也就是说，在目标领域中多次复制源模型的预测头部。并为它们的输入图像和特征映射添加一系列随机扰动（例如，Dropout，空间变换），以获得多个不同的分割预测。然后，通过这些预测的集成来获取目标领域图像的伪标签。为了抑制潜在不正确的伪标签的影响，引入了集成方法和 MC dropout 不确定性估计来获得可靠性 Map。可靠像素的伪标签用于监督每个预测头部的输出，而不可靠像素的预测则通过平均预测图上的熵最小化进行规范化。

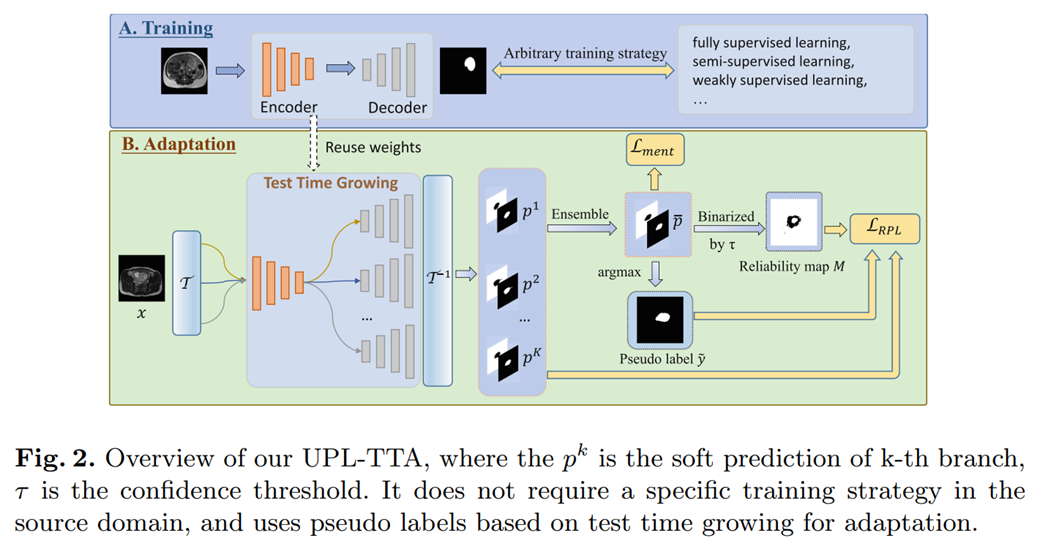
具体实现¶

Pre-trained Model from the Source Domain¶

第一步我们需要优化一个源域的预训练模型，即 Fig. 2 的 A 部分，${\theta}_g^0$ 和 ${\theta}_h^0$ 分别表示编码器和解码器的初始权重： $$ \theta_g^0, \theta_h^0=\arg \min {\theta_g, \theta_h} \frac{1}{N_s} \sum{i=1}^{N_s} L_s\left(h\left(g\left(\boldsymbol{x}_i^s\right)\right), y_i^s\right) $$

Test-Time Growing for Adaptation¶

对于 TTG 的过程，首先对于一张图像 $x$ 首先需要一个空间变换 $\mathcal{T}$，包括随即翻转，旋转 π/2，π 和 3π/2。然后经过 Dropout（特征级别的扰动）后在输入到 decoder中，再进行空间变换逆过程，得到概率图。 $$ \boldsymbol{p}^{k=\mathcal{T}}{-1} \circ h^k(g(\mathcal{T} \circ x)) $$ 上面概述里我们提到过，通过在目标领域中多次复制源模型的预测头部，并为它们的输入图像和特征映射添加一系列随机扰动（例如，Dropout，空间变换），以获得多个不同的分割预测。最后，对 K 个头进行集成： $$ \overline{\boldsymbol{p}}=\frac{1}{K} \sum_{k=1}^K \boldsymbol{p}^k $$

Supervision with Reliable Pseudo Labels¶

这一步我们关注如何获得一个可靠的伪标签。Fig. 2 中的 Reliable map $M$ 简单理解为一个 Mask，用于优化伪标签。设定一个 $\tau \in(1 / C, 1.0)$ 的阈值，我们通过对概率图的值大小确定 $M$ 的每个像素的值，只保留伪标签中较高可信度的像素： $$ M_n= \begin{cases}1 & \text { if } \overline{\boldsymbol{p}}{c^*, n}>\tau \ 0 & \text { otherwise }\end{cases} $$ 到这里我们会得到三个目标，一个是 K 个头输出的预测图，第二个是伪标签，还有用于优化伪标签的 Mask： $$ \mathcal{L}{R P L}=\frac{1}{K} \sum_{k=1}^K \mathcal{L}_{w-\text { dice }}\left(\boldsymbol{p}^k, \tilde{y}, M\right) $$

Mean Prediction-Based Entropy Minimization¶

熵最小化是 TTA 中很常用的手段，但是在 UPL-TTA 中，我们有 K 个集成。假设一种情况，第 K-1 个头的的预测概率是 0，第 K 个头的预测概率是 1，这时两个头的熵值都是最小的，但是一旦平均下来之后，0.5 对应的熵就是大的。所以我们需要同时熵最小化 K 个头： $$ \mathcal{A m e n t}m=-\frac{1}{H W} \sum{n=1}^{H W} \sum_{c=1}^C \overline{\boldsymbol{p}}{c, n} \log \left(\overline{\boldsymbol{p}}{c, n}\right), $$

Adaptation by Self-training¶

最后，我们的优化目标是下面两个损失： $$ \mathcal{L}=\mathcal{L}{R P L}+\lambda \mathcal{L}{\text {ment }} . $$

实验¶

数据集：

和其他 SOTA 方法的对比：

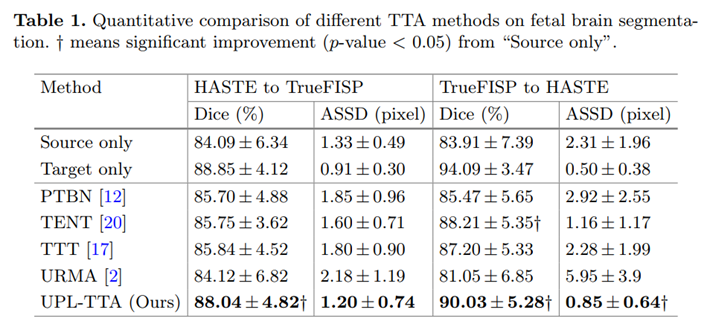
可视化结果：

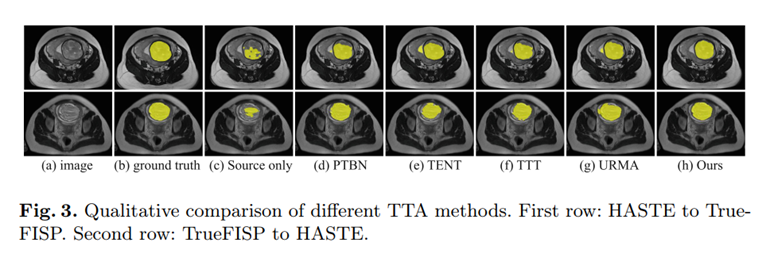
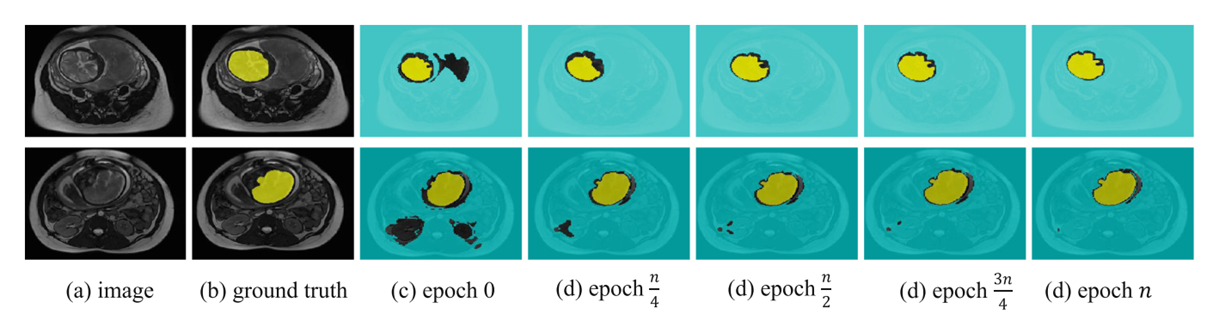
下图是自训练中不同训练步骤的伪标签。Epoch 0 表示“仅源域”（自适应之前），n 表示目标域验证集上的最佳轮数。在（c）-（g）中，只有可靠的伪标签用颜色编码。

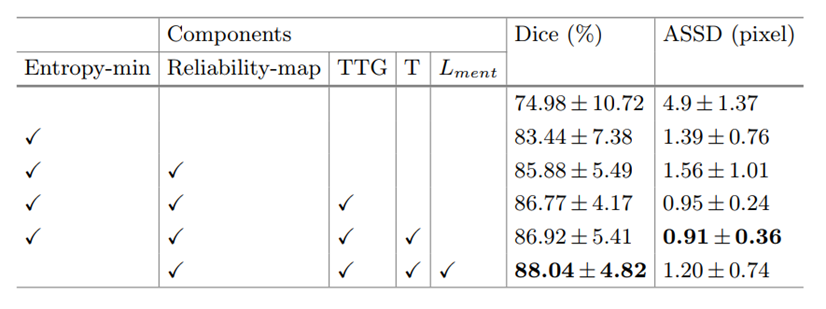
消融实验：

总结¶

这篇 IPMI 2023 工作提出了一种完全测试时间自适应的方法，该方法能够在不知道源模型的训练策略的情况下，将源模型适应到未标记的目标域。在没有访问源域图像的情况下，提出的基于不确定性的伪标签引导的 TTA 方法通过测试时间增长（TTG）为目标域中的同一样本生成多个预测输出。它生成高质量的伪标签和相应的可靠性Map，为未标记的目标域提供有效的监督。具有不可靠伪标签的像素通过对复制的头部的平均预测进行熵最小化进一步规范化，这也引入了隐式的一致性规范化。在胎儿脑分割的双向跨模态 TTA 实验中，优于几种最先进的 TTA 方法。未来，实现该方法的 3d 版本并将其应用于其他分割任务是很有兴趣的方向（事实上已经扩展到期刊了，等待见刊 ing）。