ImgX-DiffSeg:基于 DDPMs 的 3D 医学图像分割¶
目录¶
- 前言
- 目前存在的问题
- ImgX-DiffSeg 架构
- 概述
- DDPM with Variance Schedule Resampling
- Diffusion Model for Segmentation
- 实验
- 总结
- 参考
前言¶
本篇文章继续解读医学图像 diffusion 系列,之前我们分别介绍过在自监督和有监督分割中的 diffusion 应用。链接:
而这次的《Importance of Aligning Training Strategy with Evaluation for Diffusion Models in 3D Multiclass Segmentation》这篇文章并不是一种新的 diffusion 应用,而是对训练和推理策略进行优化,并适应 3D 的医学图像分割任务,参考链接在文末。
目前存在的问题¶
- 目前带有 diffusion model 的架构训练和推理耗时。
- 在一些分割任务中,并不确定 diffusion model 预测噪声推断分割图和直接预测分割图哪个效果更好。
- 模型过度依赖先前时间步中的信息。
ImgX-DiffSeg 架构¶
概述¶
DDPM 是一种生成模型,可用于图像去噪和分割。工作原理是模拟干净图像的概率分布,然后在图像中添加噪点以生成噪声版本。相反的,模型尝试通过移除添加的噪点来对图像进行降噪。在图像分割的情况下,模型会生成分割掩码,可以根据输入图像的特征将图像分成不同的区域,更细节的内容推荐阅读前置文章(强烈建议)。
对于 ImgX-DiffSeg,整体流程如下图所示。首先,该架构预测的是分割掩码而不是采样噪声,并直接通过 Dice Loss 进行优化。这意味着 ImgX-DiffSeg 可以直接预测图像的分割图,而不是生成噪点并用它来推断分割。其次,回收上一个时间步中预测的掩码,生成(noise-corrupted mask)噪音损坏的掩码。这有助于减少信息泄露,当模型过度依赖先前时间步中的信息时,就会发生这种情况。最后,将训练的扩散过程减少到五个步骤,与推理过程相同。扩散过程是一种平滑图像中噪点的方法,减少步骤数有助于提高效率。
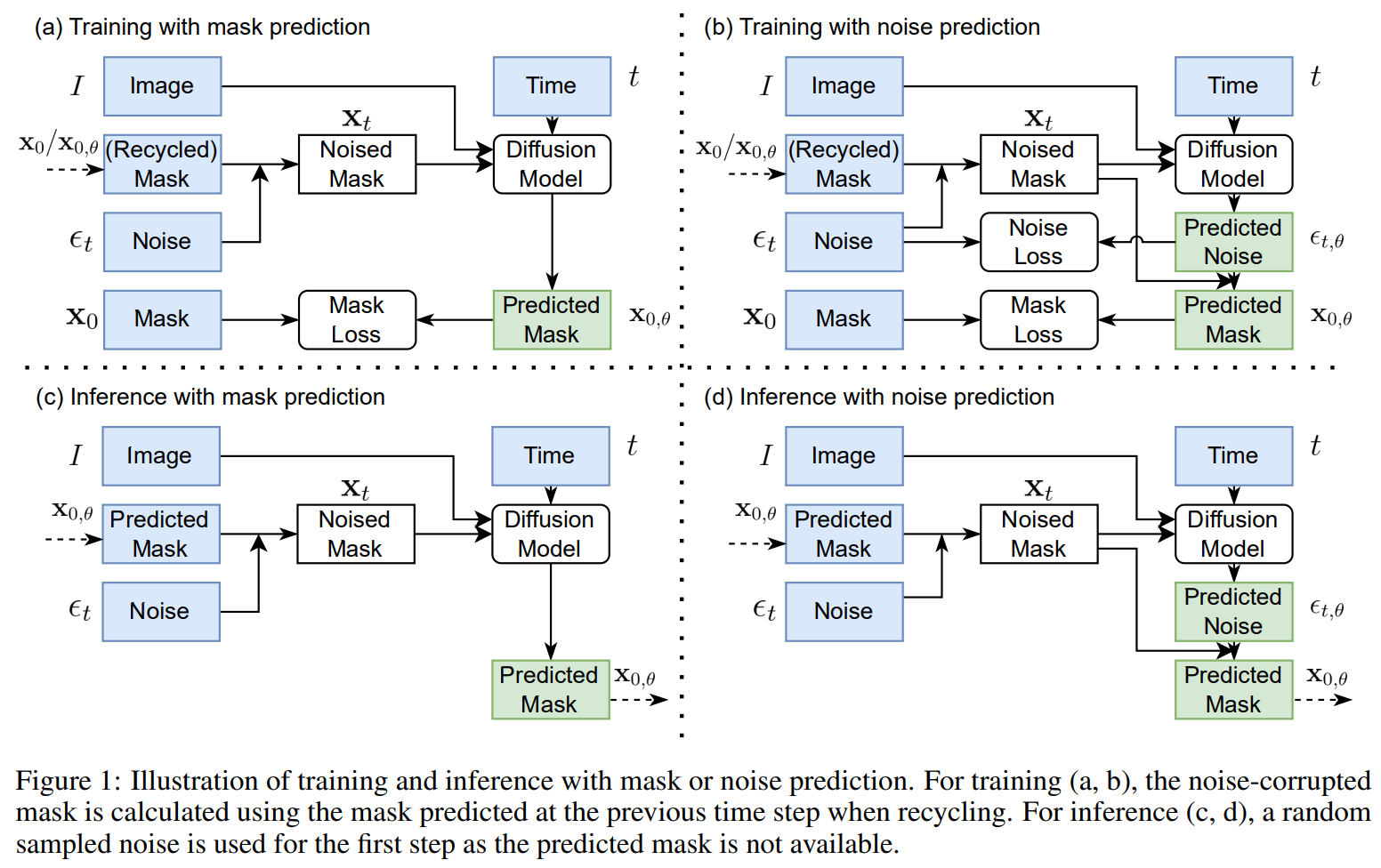
DDPM with Variance Schedule Resampling¶
训练过程的公式和 DDPM 基本是保持一致的,下面的公式分别表示反向过程中预测噪声和原图: $$ \begin{aligned} & L_{\text {simple }, \epsilon_l}(\theta)=\mathbb{E}{t, \mathbf{x}_0, \epsilon_t}\left|\epsilon_t-\epsilon{t, \theta}\left(\mathbf{x}t\left(\mathbf{x}_0, \epsilon_t\right), t\right)\right|_2^2,\left(\text { Predict } \epsilon_t\right) \ & L{\text {simple }, \mathbf{x}0}(\theta)=\mathbb{E}{t, \mathbf{x}0, \epsilon_t}\left|\mathbf{x}_0-\mathbf{x}{0, \theta}\left(\mathbf{x}t\left(\mathbf{x}_0, \epsilon_t\right), t\right)\right|_2^2 .\left(\text { Predict } \mathbf{x}_0\right) \end{aligned} $$ 推理过程中,DDPM 中的生成过程从正常噪声开始,由变量 xT 表示。该初始噪声是从平均值为 0 且方差为 1 的正态分布中采样的。在生成过程的每个步骤中,使用预测的平均值 µ 对变量 xtk-1 进行采样。下标 k-1 表示上一个时间步。这意味着每步 x 的值取决于上一步中 x 的值以及分布的预测平均值。 $$ \begin{aligned} p\theta\left(\mathrm{x}{t-1} \mid \mathrm{x}_t\right) & =\mathcal{N}\left(\mathrm{x}{t-1} ; \boldsymbol{\mu}\theta\left(\mathrm{x}_t, t\right), \sigma_t^2 \mathrm{I}\right), \ \mu\theta\left(\mathrm{x}t, t\right) & \left.=\frac{1}{\sqrt{\alpha}}\left(\mathrm{x}_t-\frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}} \epsilon{t, \theta}\left(\mathrm{x}t, t\right)\right), \text { (Predict } \epsilon_t\right) \ \mu\theta\left(\mathrm{x}t, t\right) & =\frac{\sqrt{\bar{\alpha}{t-1}} \beta_t}{1-\bar{\alpha}t} \mathrm{x}{0, \theta}\left(\mathrm{x}t, t\right)+\frac{1-\bar{\alpha}{t-1}}{1-\bar{\alpha}_t} \sqrt{\alpha_t} \mathrm{x}_t .\left(\text { Predict } \mathrm{x}_0\right) \end{aligned} $$ 上面这些流程均和 DDPM 相似,我们就不展开说明了。重点关注 Variance Schedule Resampling 的过程,也就是如何实现训练的扩散过程减少到五个步骤的。可以理解为对方差值子序列进行采样的过程。给出了方差表 {βt} Tt=1,子序列 {βk} Kk=1 可以用 {tk} Kk=1 进行采样。简而言之,在训练或推理过程中,给出方差值序列,并对这些值的子序列进行采样。子序列中的值是根据先前的值和重新计算的值计算的。目标是通过在训练或推理期间调整方差值来优化模型的性能。如果是在图像去噪任务中进行方差的重采样,一定会影响结果,但在分割任务中经过验证是有效的。
Diffusion Model for Segmentation¶
上一部分是对 DDPM 的方差重采样,不涉及到图像分割过程。对于分割任务上的优化,ImgX-DiffSeg 可以依据时间步,使用预测噪声和采样噪声之间的 L2 损失进行训练。此外,ImgX-DiffSeg 计算预测掩码和金标准之间定义的特定分割损失,例如 Dice Loss 或 CE Loss。 $$ L_{\mathrm{scg}, \boldsymbol{\epsilon}t}(\theta)=\mathbb{E}{t, \mathbf{x}0, \boldsymbol{\epsilon}_t, I}\left|\boldsymbol{\epsilon}_t-\boldsymbol{\epsilon}{t, \theta}\left(\mathbf{x}_t, t, I\right)\right|_2^2 $$
在训练期间,现有方法通过插值噪声和金标准对噪声掩模进行采样,这会导致数据信息丢失。为了解决这个问题,模型在上一个时间步中的预测被回收以取代金标准。回收的噪声掩码是使用下面方程计算的。 $$ \begin{aligned} \mathbf{x}t & =\sqrt{\bar{\alpha}_t} \mathbf{x}{0, \theta}\left(\mathbf{x}{t+1}, t+1, I\right)+\sqrt{1-\bar{\alpha}_t} \epsilon_t \ \mathbf{x}{t+1} & =\sqrt{\bar{\alpha}{t+1}} \mathbf{x}_0+\sqrt{1-\bar{\alpha}{t+1}} \epsilon_{t+1} \end{aligned} $$ 其中, x0theta 是使用金标准计算的上一个时间步的预测分割掩码,xt 和 xt+1 是两个独立的采样噪声。梯度停止应用于 xt+1 以防止通过回收的噪声掩码进行反向传播。αt 是超参数。第一个方程使用先前的预测和当前噪声计算 xt,而第二个方程使用金标准和下一个噪声计算 xt+1。
实验¶
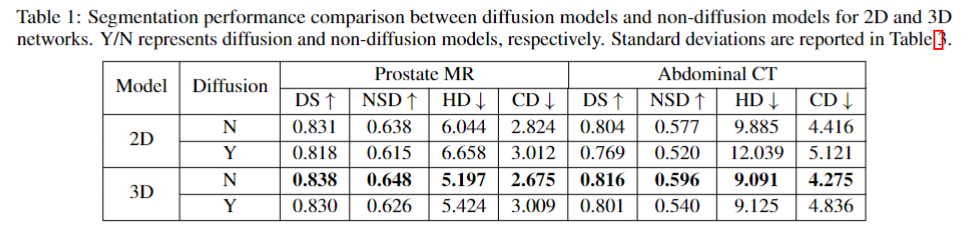
实验分别基于 MRI 和 CT 图像数据集, 值得注意的是,ImgX-DiffSeg 在 3D 上的表现是好于 2D 数据集的,如下表所示。
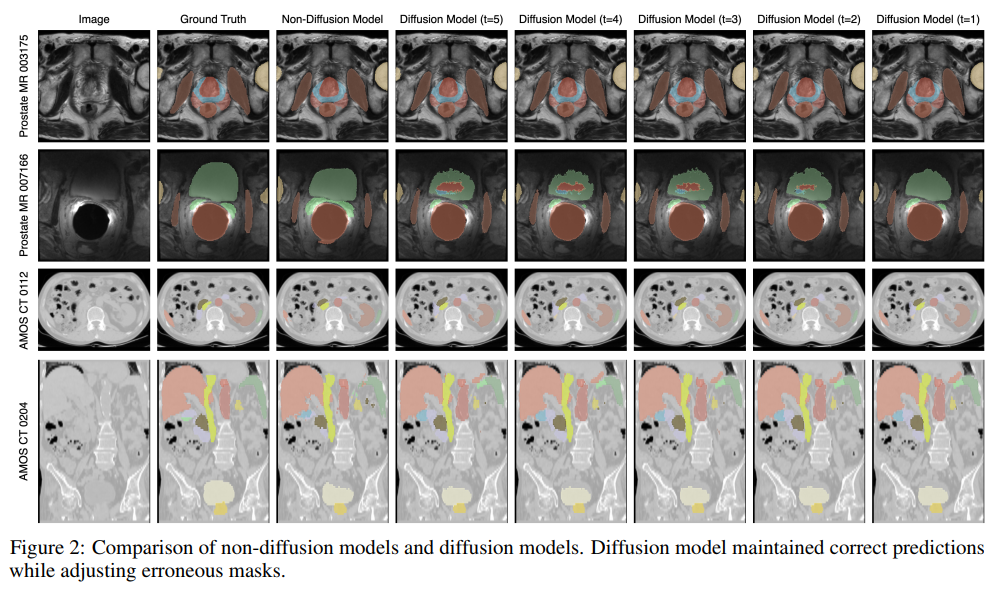
下图是非扩散分割模型和扩散概率模型之间的可视化比较,其中 t 表示时间步,一直反向扩散到第一个时间步的效果最好。
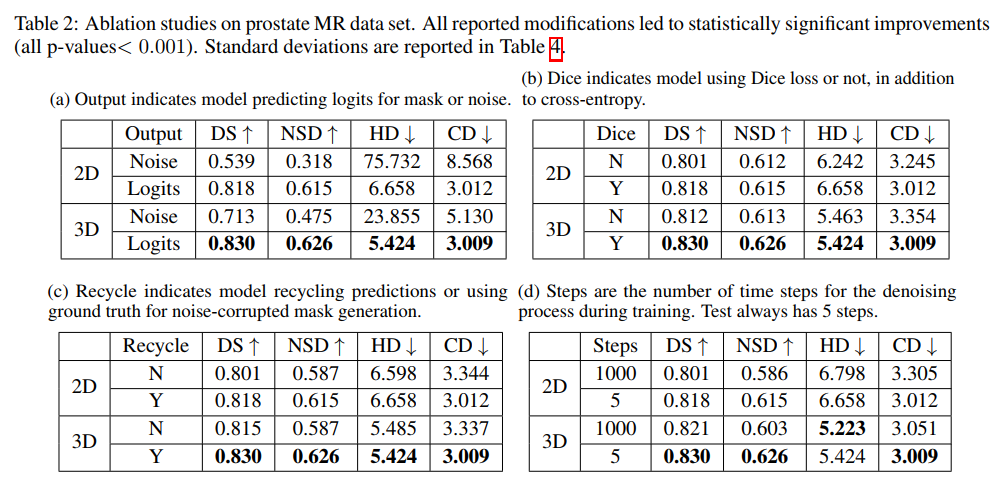
下表是四种消融实验,分别是预测噪声推断分割图和直接预测分割图对比;损失函数对比;是否回收上一个时间步中预测的掩码对比;训练过程的时间步数量对比。5 个 steps 的效果优于 1000 个 steps,说明 Variance Schedule Resampling 是有效果的。
总结¶
ImgX-DiffSeg 是第一个用于 3D 图像多类分割的 DDPM 模型,与现有的基于扩散的方法相比,该模型显著提高了性能,但也没有优于普通的非扩散分割模型,还值得进一步改进。这篇文章的代码目前已开源,我试了一下,训练的收敛速度真的快,可以作为一个不错的 benchmark。
参考¶
本文总阅读量次