Instance-Conditioned GAN (NeurIPS 2021)¶

1. 论文信息¶

标题：Instance-Conditioned GAN

作者：Arantxa Casanova, Marlene Careil, Jakob Verbeek, Michal Drozdzal, Adriana Romero Soriano

原文链接：https://proceedings.neurips.cc/paper/2021/hash/e7ac288b0f2d41445904d071ba37aaff-Abstract.html

代码链接：https://github.com/facebookresearch/ic_gan

2. 背景介绍¶

首先需要介绍一种经典的非参估计的方法——核密度估计，Kernel Density Estimation(KDE).

和参数估计不同，非参数估计并不加入任何先验知识，而是根据数据本身的特点、性质来拟合分布，这样能比参数估计方法得出更好的模型。核密度估计就是非参数估计中的一种，由Rosenblatt (1955)和Emanuel Parzen(1962)提出，又名Parzen窗（Parzen window）。Ruppert和Cline基于数据集密度函数聚类算法提出修订的核密度估计方法。而非参数估计恰恰由于没有对各种分布予以假设，所以可以很好地处理复杂数据集的分布状态。

参考：

https://blog.csdn.net/unixtch/article/details/78556499

对于KDE，依照数据集的概率密度函数可以写为:

$f(x)=\lim _{h \rightarrow 0} \frac{F(x+h)-F(x-h)}{2 h}$

$\mathrm{f}(\mathrm{x})$ 的估计可以写成:

$\begin{aligned} &\hat{f}_{h}(x)=\frac{1}{2 h} \frac{\# x_{i} \in[x-h, x+h]}{N}=\frac{1}{2 N h} \sum_{i=1}^{N} 1\left(x-h \leq x_{i} \leq x+h\right)=\frac{1}{N h} \sum_{i=1}^{N} \frac{1}{2} \\ &\cdot 1\left(\frac{\left|x-x_{i}\right|}{h} \leq 1\right) \end{aligned}$

上面的这个估计得到的密度函数Q不是光滑的。如果记 $K_{0}(t)=\frac{1}{2} \cdot 1(t<1)$ ，那/估计式Q可以表示为:

$\hat{f}_{h}(x)=\frac{1}{N h} \sum_{i=1}^{N} K_{0}\left(\frac{x-x_{i}}{h}\right)$

KDE密度函数的积分:

$\int f(x) d x=\frac{1}{N h} \sum_{i=1}^{N} \int K_{0}\left(\frac{x-x_{i}}{h}\right) d x=\frac{1}{N} \sum_{i=1}^{N} \int K_{0}(t) d t=\int K_{0}(t) d t$

因而只要 $K$ 的积分等于 1 ，就能保证估计出来的密度函数积分等于 1 。若用标准正态分布的密度函数作为 $K$ ，KDE就变成了:

$\hat{f}_{h}(x)=\frac{1}{n h} \sum_{i=1}^{N} \phi\left(\frac{x-x_{i}}{h}\right)$

再回顾一下GAN，GAN的基本原理其实非常简单，这里以生成图片为例进行说明。假设我们有两个网络，G（Generator）和D（Discriminator）。正如它的名字所暗示的那样，它们的功能分别是：

G是一个生成图片的网络，它接收一个随机的噪声z，通过这个噪声生成图片，记做G(z)。
D是一个判别网络，判别一张图片是不是“真实的”。它的输入参数是x，x代表一张图片，输出D（x）代表x为真实图片的概率，如果为1，就代表100%是真实的图片，而输出为0，就代表不可能是真实的图片。

但是可以看到KDE的概率密度求解是相对来讲直接但难以优化的，尤其是在高维空间上更难以预测和估计。而其实GAN最大的优势就是不需要复杂的各种分布和核函数假设，能够通过对抗生成学习这一范式强行把概率分布拟合出来。而所以本文基于KDE这一high-level的idea，利用GAN拟合出密度函数。

3. 介绍¶

生成对抗网络(GANs)在无条件图像生成中表现出了非常好的效果。但尽管它们取得了成功，但GANs存在优化困难，并可能遭受模式崩溃，导致生成器无法获得良好的分布覆盖，经常产生质量较差和/或多样性较低的生成样本。但复杂的数据分布仍然是unconditional GANs比较难处理的情况。Classconditional GANs通过对类标签进行条件反射，简化了学习数据分布的任务，有效地对数据进行了划分。虽然它们提供的样品比无条件的样品质量更高，但它们需要有标签的数据，而这些数据可能无法获得或获取成本很高。所以本文探索了在缺失label的情况下如何进行GANs的训练，同时保证生成样本的多样性。

作者提出了一种训练 GAN 的新方法，他们称之为Instance-Conditioned GAN。这种方法类似于Conditioned GAN，但不是使用标签，而是使用从某些特征函数中提取的特征向量（通过在实验中使用 ResNet50）。这绕过了Conditioned GAN 对标签的需求。但是，还有另一个区别。假设特征是局部相似的，因此在评估loss时，选择真实图像作为给定实例的邻居。这创建了一个核密度估计类型的模型。取得了非常不错的效果。

在这项工作中，我们引入了一种新的方法，称为实例条件GAN (IC-GAN)，它扩展了GAN框架，以模型混合本地数据密度。更准确地说，IC-GAN通过提供实例的表示作为生成器和鉴别器的额外输入，并使用实例的邻居作为鉴别器的真实样本，学习对数据点(也称为实例)的邻域分布建模。通过在条件反射的实例周围选择一个足够大的邻域，方法就避免了模型总是被小类所吸引而导致模型坍塌。

4. 方法介绍¶

IC-GAN的关键思想是通过利用数据流形中的细粒度重叠簇来模拟复杂数据集的分布，其中每个簇由一个数据点 $x_{i}$ 描述，被称为instance，和它最近的 nearest neighbors，定义为 $A_{i}$ ，其存在一个特征空间。我们的目标是将底层数据分布 $p(x)$ 建模为数据集中M个实例特征向量 $h_{i}$ 周围的条件分布 $p(x | h_{i})$ 的混合分布。

IC-GAN可以看作是一种类似于KDE的非参数估计的方式进行探索，其中每个分量都是通过对训练实例进行条件化估计计算出来的得到的。KDE的核以及选取的内参点等变量都会显著影响最后的收敛结果，同时由于KDE本身采用的优化方式也很难处理大数据量的情况，所以KDE一直无法与基于深度学习的方式相结合。所以与KDE不同的是，IC-GAN 不对数据概率进行显式的建模，而是采用了一种对抗性的方法，其中我们使用一个神经网络来隐式地对局部密度进行建模，该神经网络将条件实例和噪声向量作为输入。

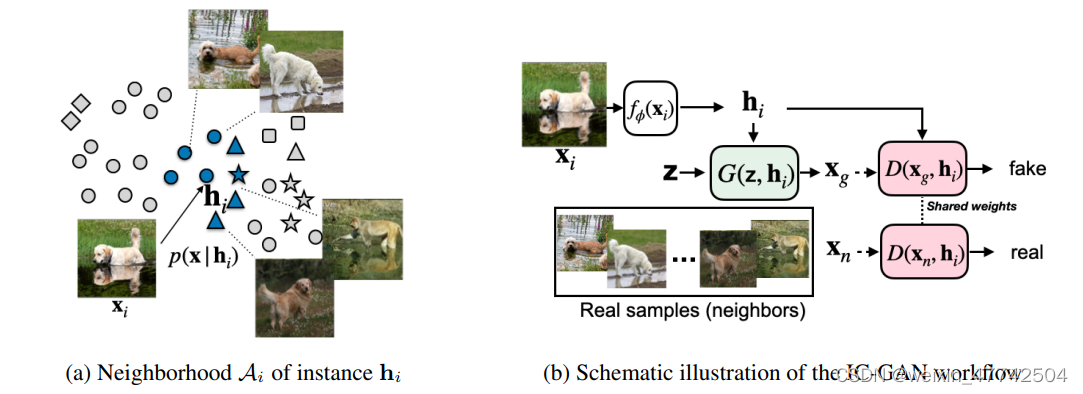
因此，IC-GAN中的内核不再独立于我们所处理的数据点，我们通过选择实例的邻域大小来控制平滑度，而不是内核带宽参数，我们从中采样真实样本以馈送到鉴别器。IC-GAN 将数据流形划分为由数据点及其最近邻描述的重叠邻域的混合物，IC-GAN模型能够学习每个数据点周围的分布。通过在条件实例周围选择一个足够大的邻域，可以避免将数据过度划分为小的聚类簇。当给定一个具有M个数据样本的未标记数据集的嵌入函数f，首先使用无监督或自我监督训练得到f来提取实例特征（instance features）。然后使用余弦相似度为每个数据样本定义k个最近邻的集合。

训练自然就是按照经典的GAN的训练模式：

$\begin{aligned} \min _{G} \max _{D} & \mathbb{E}_{\mathbf{x}_{i} \sim p(\mathbf{x}), \mathbf{x}_{n} \sim \mathcal{U}\left(\mathcal{A}_{i}\right)}\left[\log D\left(\mathbf{x}_{n}, f_{\phi}\left(\mathbf{x}_{i}\right)\right)\right]+\\ & \mathbb{E}_{\mathbf{x}_{i} \sim p(\mathbf{x}), \mathbf{z} \sim p(\mathbf{z})}\left[\log \left(1-D\left(G\left(\mathbf{z}, f_{\phi}\left(\mathbf{x}_{i}\right)\right), f_{\phi}\left(\mathbf{x}_{i}\right)\right)\right)\right] . \end{aligned}$

作者还设计了一种方式利用有label的情况进行GAN的训练，其实区别不大，就在于特征的提取器是有监督还是无监督。

5. 实验结果¶

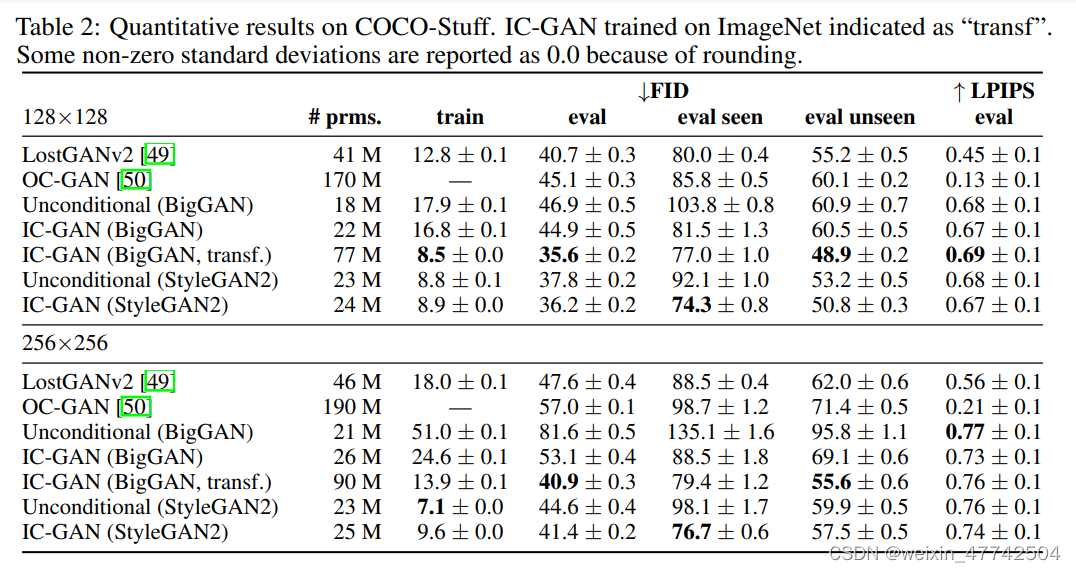
在ImageNet和COCO这个数量级的数据集中也有比较出色的表现。

6. 结论¶

本文介绍了 Instance Conditioned GAN (IC-GAN)，旨在以无条件的方式对复杂的多模态分布进行建模。该模型将目标分布划分为通过调节单个训练点及其最近邻而学习的子分布。IC-GAN 使用各种架构改进了 ImageNet 和 COCO-stuff 上的无条件图像性能基线。作者扩展了模型以执行类条件生成和迁移学习。

本文总阅读量次