【GiantPandaCV导语】最近在整理一些编译器方面的基础知识翻译，回顾了一下TVM的Schedule然后想起自己1年前做的一些GEMM相关的实验和探索没做什么总结。所以基于TVM的三个教程也即TVM的三代优化来做对之前的学习做一个简单的总结，在本篇文章中我原创的内容主要集中在对各个Schedule的单独详解以及引入了TIR的伪代码描述帮助读者更好的理解TVM Schedule。还有深入解读了Blocking技术以及Auto Schedule搜出的高性能程序，简要分析了micro Kernel的汇编。另外我制作了一个控制Schedule变量进行测试得到的GFLOPS柱状图，方便大家对比各代优化的效果。感慨一下，我认为当前做优化的人以及独特的优化技巧都绝不在少数。如果基于通用的自动代码生成就可以达到任意硬件GFLOPS的80-90%，那么深度学习编译器可能就真的“收敛”了。但毕竟基于Ansor在Jetson Nano上搜一下GEMM的优化程序，性能非常差是我实验过的一个事实。无论是编译器还是深度学习框架对某些常见场景有过拟合是可以理解的，这并不妨碍Ansor是一个非常优秀的工作。我个人觉得我们对深度编译器的看法不能过于激进，目前深度学习编译器在代码生成上上仍然处于一个半自动状态，应该没有任何一家做业务的公司可以放心把各种要上线的业务的性能交给编译器来保证，所以应当稳中求快好一点。和性能快慢相比，我个人现阶段最在意的事情是代码是否鲁棒，很多情况下代码写正确且稳定运行的难度不小于一些优化的奇淫技巧。综上，请辩证的看待本篇文章中隐含的个人想法，包括对此提出批评。如果你读完本文觉得对你有一点用的话欢迎点一个赞，整理这篇文章陆续花了我2天时间。本文相关代码都在：https://github.com/BBuf/tvm_mlir_learn ，欢迎大家star我这个仓库一起学习TVM和MLIR，目前已经有近400个Star了。如果本篇文章点赞能过百，后面会考虑出一篇解读TVM CUDA优化教程的类似文章。请多多点赞，thanks!

0x0. 前言¶

本文主要梳理一下在21年接触到优化gemm的知识，做一个学习总结。行文的顺序大概为：

介绍本文依赖的硬件环境和本文要完成的任务。
回顾gflops的计算方法并计算本地机器的GFLOPS。
RoofLine模型。
How to optimize GEMM on CPU 教程讲解。(https://github.com/apache/tvm/blob/main/gallery/how_to/optimize_operators/opt_gemm.py) 并细致梳理每一种优化方法的作用以及它们在IR中的表示。
Optimizing Operators with Schedule Templates and AutoTVM 教程讲解。（https://github.com/apache/tvm/blob/main/gallery/tutorial/autotvm_matmul_x86.py）
Optimizing Operators with Auto-scheduling 教程讲解。（https://github.com/apache/tvm/blob/main/gallery/tutorial/auto_scheduler_matmul_x86.py）
总结。

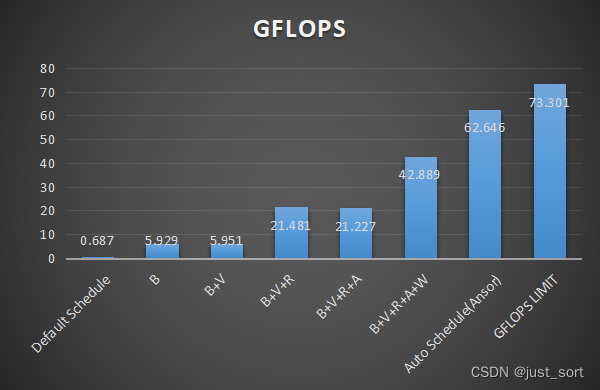
先放一张总览图：

基于Auto Schedule得到的最好结果，搜索了20分钟

0x1. 本文依赖的硬件环境以及本文要完成的任务¶

本文的相关实验以及测试数据在同一硬件环境以及Ubuntu操作系统中完成，下图为机器的配置硬件信息如下：

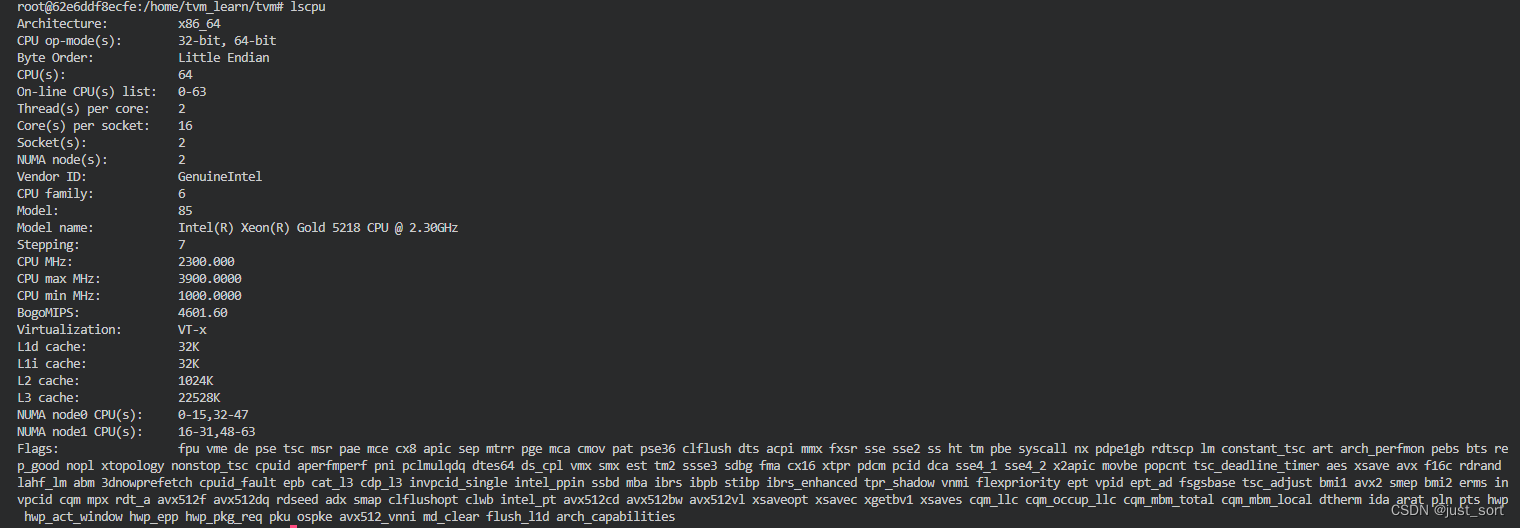
机器的配置信息

注意到此CPU的核心为64，主频的最大值最小值分别为3900和1000Mhz，以及L1d，L2，L3 cache的大小分别为32K，1024K，22528K。

接下来说一下本文要完成的任务是什么？非常简单，本文的任务就是实现 $C=A*B$ ，其中 $C$ 的维度是 $[m, n]$ ， $A$ 的维度是 $[m,k]$ ， $B$ 的维度是 $[k, n]$ ，那么矩阵乘法的原始实现就是：

// gemm C = A * B + C
void MatrixMultiply(int m, int n, int k, float *a, float *b, float *c)
{
    for(int i = 0; i < m; i++){
        for (int j=0; j<n; j++ ){    
            for (int p=0; p<k; p++ ){      
                C(i, j) = C(i, j) + A(i, p) * B(p, j);
            }
        }
    }
}

为了让这个问题更加简单，在本文我们约定m，n，k的值都为1024。

0x2. 回顾GFLOPS的计算方法并计算本地机器的GFLOPS¶

FLOPs：注意s小写，是FLoating point OPerations的缩写（s表复数），意指浮点运算数，理解为计算量。可以用来衡量模型的复杂度。针对神经网络模型的复杂度评价，应指的是FLOPs，而非FLOPS。 FLOPS：注意全大写，是floating point operations per second的缩写，意指每秒浮点运算次数，理解为计算速度。是一个衡量硬件性能的指标。比如nvidia官网上列举各个显卡的算力（Compute Capability）用的就是这个指标。

在讲解TVM的几个教程之前，我们需要先来计算一下机器的GFLOPS并以此判断后面几种TVM教程中生成的GEMM代码的性能相比于硬件浮点峰值大概到达了什么水平。

浮点峰值一般是计算单位时间内乘法和加法的最大吞吐量，单位为GFLOPS或者TFLOPS，表示每一秒可以计算的乘法和加法的总次数。我们可以根据硬件的结构计算一个理论的浮点峰值，并且也可以基于汇编指令来实测硬件的浮点峰值。由于对这一款CPU的架构了解比较有限，我们这里就直接来实测浮点峰值，后续的讲解基本也只和实测的浮点峰值有关。

基于高叔叔的https://github.com/pigirons/cpufp 进行测试，这里的基本原理是在循环内安排尽可能多的无数据依赖的乘加汇编指令掩盖因寄存器依赖浪费的时间周期，具体见：https://zhuanlan.zhihu.com/p/28226956。我们执行如下命令进行测试：

git clone git@github.com:pigirons/cpufp.git
sh build.sh
./cpufp num_threads

分别测试num_threads=1，2，4时的GFLOPS，也即单核心，双核心以及四核心的GFLOPS。结果如下：

Thread(s): 1
avx512_vnni int8 perf: 267.7062 GFLOPS.
avx512f fp32 perf: 66.9300 GFLOPS.
avx512f fp64 perf: 33.4678 GFLOPS.
fma fp32 perf: 73.3017 GFLOPS.
fma fp64 perf: 36.6564 GFLOPS.
avx fp32 perf: 36.6528 GFLOPS.
avx fp64 perf: 18.3270 GFLOPS.
sse fp32 perf: 22.3124 GFLOPS.
sse fp64 perf: 11.1580 GFLOPS.

Thread(s): 2
avx512_vnni int8 perf: 535.5030 GFLOPS.
avx512f fp32 perf: 133.8812 GFLOPS.
avx512f fp64 perf: 66.9439 GFLOPS.
fma fp32 perf: 146.6221 GFLOPS.
fma fp64 perf: 73.3141 GFLOPS.
avx fp32 perf: 73.3229 GFLOPS.
avx fp64 perf: 36.6583 GFLOPS.
sse fp32 perf: 44.6286 GFLOPS.
sse fp64 perf: 22.3151 GFLOPS.

Thread(s): 4
avx512_vnni int8 perf: 1070.9130 GFLOPS.
avx512f fp32 perf: 267.7571 GFLOPS.
avx512f fp64 perf: 133.8734 GFLOPS.
fma fp32 perf: 293.1998 GFLOPS.
fma fp64 perf: 146.6209 GFLOPS.
avx fp32 perf: 146.6289 GFLOPS.
avx fp64 perf: 73.3129 GFLOPS.
sse fp32 perf: 89.2652 GFLOPS.
sse fp64 perf: 44.6303 GFLOPS.

容易观察到GFLOPs和CPU核心数是一个正比例的关系。本文的优化只关注在单核心上，后面的程序都使用os.environ['TVM_NUM_THREADS']=str(1) 将程序绑定在一个CPU核心上。

0x3. RoofLine模型¶

上面已经介绍了GFLOPs（1GFLOPs=10^9FLOPs）和GFLOPS的概念，这里要简单引入一下计算密度和RoofLine模型。所谓计算密度指的是单位访存量下所需的计算量，单位是 FLOPs/Bytes。对于本文的任务来说，FLOPs即浮点的计算次数为 $2 \times 1024 \times 1024 \times 1024 = 2.147GFLOPs$ ，这里的Bytes指的是访存量，在这个例子中访存量是 $3*1024*1024*sizeof(float)=12MB=0.0117GB$ ，所以这里的计算密度为 $2.147GFLOPs/0.0117GB=183.5FLOPs/Bytes$ 。而RoofLine模型是一个用来评估程序在硬件上能达到的性能上界的模型，可用下图表示：

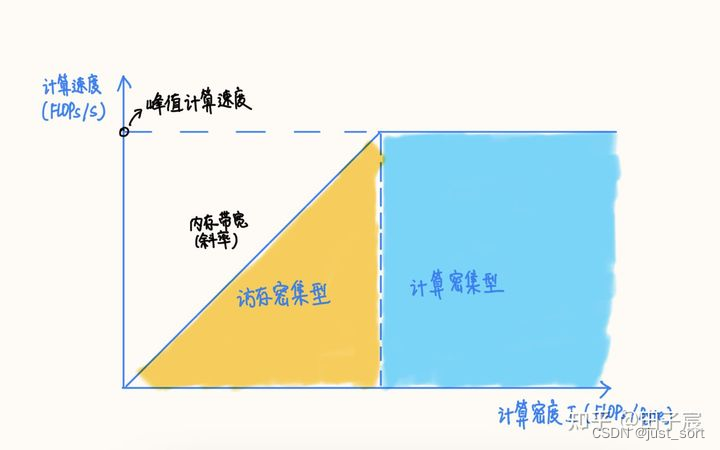
RoofLine 模型，来自RoofLine 模型

注意到我们计算出的计算密度183.5FLOPs/Bytes是远大于单核心的fma fp32 perf: 73.3017 GFLOPS的，所以很显然我们的算子是一个计算密集形算子，那么计算速度的上限就是峰值计算速度不会受制于带宽。那么我们就可以放心的进行接下来的讲解了。

指的一提的是理论上的RoofLine模型和硬件真实的RoofLine模型还有一定的Gap，以及对于矩阵乘来说某些参数的改变可能会让这个算子从计算密集型朝着访存密集形发生改变。推荐商汤田子宸兄的这篇《深度学习模型大小与模型推理速度的探讨》文章，里面对RoofLine模型做了更加详细的解释以及思考。https://zhuanlan.zhihu.com/p/411522457

Whatever，我们现在知道本文的 $1024\times 1024$ 规模的矩阵乘是一个计算密集型的算子，那我们就去看看TVM针对这种访存密集型算子相比浮点峰值可以优化到什么水平吧。

0x4. How to optimize GEMM on CPU 教程讲解。¶

这一篇教程全面讲解了TVM里面对schedule的优化方法，这些优化基本都来自于我以前介绍过的 https://github.com/flame/how-to-optimize-gemm 这个仓库，比如分块，矢量化，循环重排，Array Packing等等技巧。TVM这个教程将所有的优化技巧基本都用上了，然后直接给出了最终的结果。我觉得这对不太了解TVM的人跨度稍大。所以接下来我将逐一对这些技巧进行介绍并且逐步应用于Naive的TVM张量表达式并展示每一种优化技巧对应的TIR的变化。

这一节教程涉及到的优化技巧为：

Blocking（分块）
Vectorization（向量化）
Loop Permutation（调整分块的计算顺序）
Array Packing（数据重排）
Write cache for blocks（为写操作数据块创建连续内存缓存）
Parallel（并发运算）

接下来细说。

0x4.1 Blocking（分块）¶

Blocking通常也叫Tiling，是优化循环一种常见并且很有效的策略。我们先说一下Blocking是要解决什么问题然后我们来看是怎么解决的。看如下的例子：

int *A = new float [N];
int *B = new float[M];
for(int i = 0; i < N; i++){
    for(int j = 0; j < M; j++) {
        A[i] += B[j];
    }
}

如果这个例子中M是比较大的，那么整个算法一定是不高效的。原因在于计算机在访问数组时并不是逐个从内存中访问的，而是以CacheLine为单位去访问，CacheLine的大小一般为64K。也就是说当我们访问B[0]的时候，实际上B[0]-B[15]已经在同一个CacheLine中进而被放进了Cache中，这样访问的速度就会更快。但由于CPU的Cache时有限的，当Cache满了之后如果还要新的CacheLine要进来，那么Cache就要把旧的CacheLine驱逐出去。

比如这里M比较大，那么我们在访问B[200]的时候，B[0]对应的CacheLine已经被驱逐出缓存了，这样随着i的递增下次要重新访问B[0]就不得不再次从内存中去加载。因此整个算法由于需要循环访问的数据在缓存中频繁的换入换出，导致性能比较差。

为了解决这个问题，引入了Blocking或者叫Tiling。Blocking就是在总的数据量无法放进Cache的情况下，把总数据分成一个小块去访问，让每个Tile都可以在Cache中。具体的做法就是把一个内层循环分解成 outer loop * inner loop。然后把 outer loop 移到更外层去，从而确保 inner loop 的数据访问一定能在Cache中。

对于下面的这段代码：

for(int i = 0; i < N; i++){
    for(int j = 0; j < M; j++) {
        A[i] += B[j];
    }
}

当M比较大的时候，我们可以简单计算一下它Cache Miss的次数，对于A来说，Cache Miss的次数为 $N / B$ ，其中B的Cache Miss次数为 $M / B * N$ ，乘以N是因为i每次递增的时候，由于M很大B开头的一部分数据已经被驱逐出缓存了。这样总的Cache Miss次数就为 $N / B + M / B * N=N / B * (M + 1)$ 。

按照Blocking的解决方案，我们把内层循环for(int j = 0; j < M; j++)按T的大小来进行分解。那么上面的代码变成：

for (int j_o = 0; j_o < M; j_o += T){
    for (int i = 0; i < N; i++) {
        for (int j_i = j_o; j_i < j_o + T; j_i++){
            A[i] += B[j_i];
        }
    }
}

可以发现这里的最内层j_i循环始终可以满足在缓存中，总的CacheMiss为： $N / B * M / T$ + $T / B$ * $M / T$ = $N / B * M / T + M / B = M / B \times (N / T + 1)$ 。从数量级上看，经过一次Block的优化，Cache Miss的次数减少了T倍。

很明显我们发现循环 $i$ 现在变成了inner loop，我们同样对它进行分解。那么伪代码变成：

for (int i_o = 0; i_o < N; i_o += T){
    for (int j_o = 0; j_o < M; j_o += T) {
        for (int i_i = i_o; i_i < i_o + T; i_i++){
            for (int j_i = j_o; j_i < j_o + T; j_i++){
                A[i_i] += B[j][i];
            }
        }
    }
}

最终得到Cache Miss数量级相比于原始的循环将会减少 $T^2$ 倍。这就是Blocking或者Tiling的基本原理，通过分块降低数据访问的Cache Miss从而提升性能。接下来，我们基于TVM的教程看一下对矩阵乘算子进行Tiling得到了什么结果。

我们先补充一下TVM以默认Schedule运行矩阵乘的TIR，对应的实验代码在https://github.com/BBuf/tvm_mlir_learn/blob/main/optimize_gemm/optimize_matmul_in_gemm/tvm_without_tune_default_schedule.py：

@main = primfn(A_1: handle, B_1: handle, C_1: handle) -> ()
  attr = {"from_legacy_te_schedule": True, "global_symbol": "main", "tir.noalias": True}
  buffers = {A: Buffer(A_2: Pointer(float32), float32, [1048576], []),
             B: Buffer(B_2: Pointer(float32), float32, [1048576], []),
             C: Buffer(C_2: Pointer(float32), float32, [1048576], [])}
  buffer_map = {A_1: A, B_1: B, C_1: C} {
  for (m: int32, 0, 1024) {
    for (n: int32, 0, 1024) {
      C[((m*1024) + n)] = 0f32
      for (k: int32, 0, 1024) {
        let cse_var_2 = (m*1024)
        let cse_var_1 = (cse_var_2 + n)
        C[cse_var_1] = (C[cse_var_1: int32] + (A[(cse_var_2: int32 + k)]*B[((k*1024) + n)]))
      }
    }
  }
}

可以看到这就是简单的三重for循环嵌套，没有任何优化技巧，自然这份代码的效率也是比较低的，可以当作本文的BaseLine。我根据它的执行时间计算了GFLOPS，结果如下：

0.687 GFLOPS

然后我们看一下加了Blocking优化对应的TIR，代码在https://github.com/BBuf/tvm_mlir_learn/blob/main/optimize_gemm/optimize_matmul_in_gemm/tvm_without_tune_only_blocking.py：

@main = primfn(A_1: handle, B_1: handle, C_1: handle) -> ()
  attr = {"from_legacy_te_schedule": True, "global_symbol": "main", "tir.noalias": True}
  buffers = {A: Buffer(A_2: Pointer(float32), float32, [1048576], []),
             B: Buffer(B_2: Pointer(float32), float32, [1048576], []),
             C: Buffer(C_2: Pointer(float32), float32, [1048576], [])}
  buffer_map = {A_1: A, B_1: B, C_1: C} {
  for (m.outer: int32, 0, 32) {
    for (n.outer: int32, 0, 32) {
      for (m.inner.init: int32, 0, 32) {
        for (n.inner.init: int32, 0, 32) {
          C[((((m.outer*32768) + (m.inner.init*1024)) + (n.outer*32)) + n.inner.init)] = 0f32
        }
      }
      for (k.outer: int32, 0, 256) {
        for (k.inner: int32, 0, 4) {
          for (m.inner: int32, 0, 32) {
            for (n.inner: int32, 0, 32) {
              let cse_var_3 = (n.outer*32)
              let cse_var_2 = ((m.outer*32768) + (m.inner*1024))
              let cse_var_1 = ((cse_var_2 + cse_var_3) + n.inner)
              C[cse_var_1] = (C[cse_var_1: int32] + (A[((cse_var_2: int32 + (k.outer*4)) + k.inner)]*B[((((k.outer*4096) + (k.inner*1024)) + cse_var_3: int32) + n.inner)]))
            }
          }
        }
      }
    }
  }
}

可以看到和我们介绍的Blocking的原理差不多，通过将i, j, k三重循环分别分解为outer和inner两重新的循环对原始计算进行分块，减少Cache Miss。从TIR我们看到矩阵A被分成 $32*4$ 的小块，矩阵B被分成 $4*32$ 的小块，矩阵C被分成 $32\times 32$ 的小块，然后对C的每一个 $32\times 32$ 小块应用Naive的矩阵乘法。下面的代码是脚本种如何设置这个Schedule的。

# 计算C(M, N) = A(M, K) x B(K, N)
def matmul(M, N, K, dtype):
    # Algorithm
    k = te.reduce_axis((0, K), "k")
    A = te.placeholder((M, K), name="A", dtype=dtype)
    B = te.placeholder((K, N), name="B", dtype=dtype)
    C = te.compute((M, N), lambda m, n: te.sum(A[m, k] * B[k, n], axis=k), name="C")

    bn = 32
    kfactor = 4
    s = te.create_schedule(C.op)

    # Blocking by loop tiling
    mo, no, mi, ni = s[C].tile(C.op.axis[0], C.op.axis[1], bn, bn)
    (kaxis,) = s[C].op.reduce_axis
    ko, ki = s[C].split(kaxis, factor=kfactor)

    # Hoist reduction domain outside the blocking loop
    s[C].reorder(mo, no, ko, ki, mi, ni)
    return s, [A, B, C]

基于Blocking优化的GFLOPS为5.929 GFLOPS：

综上所述，Blocking主要通过对矩阵进行分块来缓解因为Cache容量小导致的Cache Miss，有效率提升了矩阵乘法的运行效率。

0x4.2 Vectorize（向量化）¶

接下来，我们介绍本教程中的第二个优化技巧：vectorize（向量化）。现代CPU对于浮点运算基本都是支持SIMD的运算的，所以我们可以基于这个特性对矩阵乘进行优化。vectorize把iter方向上的循环迭代替换成ramp，从而通过SIMD指令实现数据的批量计算，并且只有在数据size为常数、且分割的iter为2的幂（即满足SIMD的计算数量）时才会发生替换，是SIMD计算设备的常用Schedule。相比于Blocking的优化，在TVM张量表达式种我们只需要添加一行代码即可实现：

# Vectorization
s[C].vectorize(ni)

然后它产生的TIR如下所示：

@main = primfn(A_1: handle, B_1: handle, C_1: handle) -> ()
  attr = {"from_legacy_te_schedule": True, "global_symbol": "main", "tir.noalias": True}
  buffers = {A: Buffer(A_2: Pointer(float32), float32, [1048576], []),
             B: Buffer(B_2: Pointer(float32), float32, [1048576], []),
             C: Buffer(C_2: Pointer(float32), float32, [1048576], [])}
  buffer_map = {A_1: A, B_1: B, C_1: C} {
  for (m.outer: int32, 0, 32) {
    for (n.outer: int32, 0, 32) {
      for (m.inner.init: int32, 0, 32) {
        C[ramp((((m.outer*32768) + (m.inner.init*1024)) + (n.outer*32)), 1, 32)] = broadcast(0f32, 32)
      }
      for (k.outer: int32, 0, 256) {
        for (k.inner: int32, 0, 4) {
          for (m.inner: int32, 0, 32) {
            let cse_var_3 = (n.outer*32)
            let cse_var_2 = ((m.outer*32768) + (m.inner*1024))
            let cse_var_1 = (cse_var_2 + cse_var_3)
            C[ramp(cse_var_1, 1, 32)] = (C[ramp(cse_var_1: int32, 1, 32)] + (broadcast(A[((cse_var_2: int32 + (k.outer*4)) + k.inner)], 32)*B[ramp((((k.outer*4096) + (k.inner*1024)) + cse_var_3: int32), 1, 32)]))
          }
        }
      }
    }
  }
}

由于在最内层循环进行了向量化，相比于上一节的TIR这里最内层循环被消除了，直接用ramp来替代。另外值得注意的是，这里有一个broadcast操作，这是因为在n.inner这层循环中A的下标和这个循环本身是没有关系的，所以相当于一个标量和一个向量来做乘法。所以这里将其广播变成一个向量，可以直接利用SIMD指令做向量的乘法。

测试一下GFLOPS（运行https://github.com/BBuf/tvm_mlir_learn/blob/main/optimize_gemm/optimize_matmul_in_gemm/tvm_without_tune_blocking_vectorize.py）：

TVM Without Tune GFLOPS: 5.951689373974107

和只用Blocking优化的GFLOPS相比，略微有一点提升，不过这里幅度不大。

0x4.3 Loop Permutation（调整分块的计算顺序）¶

我们先看一下这个优化对应在Schedule上的变化是什么？代码如下：

# re-ordering
s[C].reorder(mo, no, ko, mi, ki, ni)

相比于前2个优化的schedule（s[C].reorder(mo, no, ko, ki, mi, ni)）来说，唯一的变化就是交换了 $mi$ 和 $ki$ 的位置，这有效果吗？测试一下：

TVM Without Tune GFLOPS: 21.480747047174887

可以看到GFLOPS提升了3-4倍，所以这里的关键是什么呢？我们重写一下Blocking Schedule的TIR对应的伪代码，比较好观察一点：

for m_o in range(0, M, T_m):
  for n_o in range(0, N, T_n):
    for k_o in range(0, K, T_k):
      for k_i in range(k_o, k_o + T_k):
        for m_i in range(m_o, m_o + T_m):
          for n_i in range(n_o, n_o + T_n):
            C[m_i][n_i] += A[m_i][k_i] * B[k_i][n_i]

可以发现在当前schedule中，A 是逐列访问的，这对Cache是不友好的。如果我们改变 $k_i$ 和内轴 $m_i$ 的嵌套循环顺序，A 矩阵的访问模式会对缓存更加友好。这也是为什么我们可以看到性能有较大提升的原因。

现在新的TIR表达式如下：

@main = primfn(A_1: handle, B_1: handle, C_1: handle) -> ()
  attr = {"from_legacy_te_schedule": True, "global_symbol": "main", "tir.noalias": True}
  buffers = {A: Buffer(A_2: Pointer(float32), float32, [1048576], []),
             B: Buffer(B_2: Pointer(float32), float32, [1048576], []),
             C: Buffer(C_2: Pointer(float32), float32, [1048576], [])}
  buffer_map = {A_1: A, B_1: B, C_1: C} {
  for (m.outer: int32, 0, 32) {
    for (n.outer: int32, 0, 32) {
      for (m.inner.init: int32, 0, 32) {
        C[ramp((((m.outer*32768) + (m.inner.init*1024)) + (n.outer*32)), 1, 32)] = broadcast(0f32, 32)
      }
      for (k.outer: int32, 0, 256) {
        for (m.inner: int32, 0, 32) {
          for (k.inner: int32, 0, 4) {
            let cse_var_3 = (n.outer*32)
            let cse_var_2 = ((m.outer*32768) + (m.inner*1024))
            let cse_var_1 = (cse_var_2 + cse_var_3)
            C[ramp(cse_var_1, 1, 32)] = (C[ramp(cse_var_1: int32, 1, 32)] + (broadcast(A[((cse_var_2: int32 + (k.outer*4)) + k.inner)], 32)*B[ramp((((k.outer*4096) + (k.inner*1024)) + cse_var_3: int32), 1, 32)]))
          }
        }
      }
    }
  }
}

对应的伪代码可以写成：

for m_o in range(0, M, T_m):
  for n_o in range(0, N, T_n):
    for k_o in range(0, K, T_k):
      for m_i in range(m_o, m_o + T_m):
        for k_i in range(k_o, k_o + T_k):
          for n_i in range(n_o, n_o + T_n):
            C[m_i][n_i] += A[m_i][k_i] * B[k_i][n_i]

0x4.4 Array Packing（数据重排）¶

我们先看一下要在矩阵乘法的张量表达式中加入Array Packing的Schedule是怎么做的：

# 计算C(M, N) = A(M, K) x B(K, N)
def matmul(M, N, K, dtype):
    # Algorithm
    k = te.reduce_axis((0, K), "k")
    A = te.placeholder((M, K), name="A", dtype=dtype)
    B = te.placeholder((K, N), name="B", dtype=dtype)

    bn = 32
    kfactor = 4

    packedB = te.compute(
    (N / bn, K, bn), lambda bigN, k, littleN: B[k, bigN * bn + littleN], name="packedB"
    )
    C = te.compute(
        (M, N),
        lambda m, n: te.sum(A[m, k] * packedB[n // bn, k, tvm.tir.indexmod(n, bn)], axis=k),
        name="C",
    )

    s = te.create_schedule(C.op)

    mo, no, mi, ni = s[C].tile(C.op.axis[0], C.op.axis[1], bn, bn)
    (kaxis,) = s[C].op.reduce_axis
    ko, ki = s[C].split(kaxis, factor=kfactor)

    s[C].reorder(mo, no, ko, mi, ki, ni)
    s[C].vectorize(ni)

    bigN, _, littleN = s[packedB].op.axis
    s[packedB].vectorize(littleN)
    s[packedB].parallel(bigN)
    return s, [A, B, C]

下图是Array Packing的一般性原理说明。

Array Packing的一般性原理说明

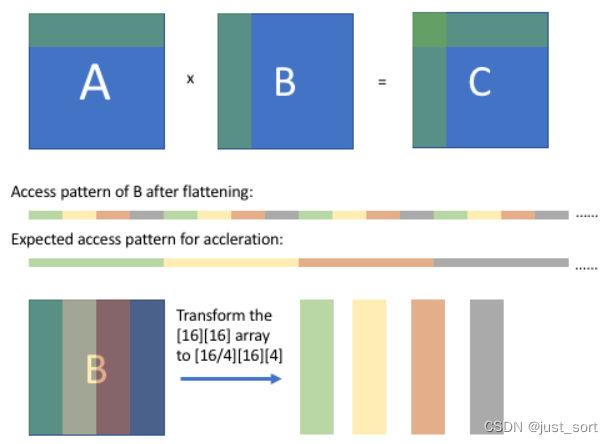
可以观察到在B展平之后，当我们在k维度迭代的时候，B数组的访问不是连续的。我们可以用对B（维度为 $[K][N]$ ）进行重排，使其具有维度 $[N/bn][K][bn]$ ，其中 bn 是分块因子，也是内循环中 B 的向量大小。这种重新排序将 N 分成两个维度 — $bigN(N/bn)$ 和 $littleN (bn)$ — 并且新维度 $[N/bn][K][bn]$ 匹配 B 从外循环到内循环的索引（no, ko, ki, ni) 所以在B被展平重排后内存访问是连续的。

加入了Array Packing Schedule对应的新TIR如下所示：

@main = primfn(A_1: handle, B_1: handle, C_1: handle) -> ()
  attr = {"from_legacy_te_schedule": True, "global_symbol": "main", "tir.noalias": True}
  buffers = {A: Buffer(A_2: Pointer(float32), float32, [1048576], []),
             B: Buffer(B_2: Pointer(float32), float32, [1048576], []),
             C: Buffer(C_2: Pointer(float32), float32, [1048576], [])}
  buffer_map = {A_1: A, B_1: B, C_1: C} {
  allocate(packedB: Pointer(global float32x32), float32x32, [32768]), storage_scope = global {
    for (bigN: int32, 0, 32) "parallel" {
      for (k: int32, 0, 1024) {
        packedB_1: Buffer(packedB, float32x32, [32768], [])[((bigN*1024) + k)] = B[ramp(((k*1024) + (bigN*32)), 1, 32)]
      }
    }
    for (m.outer: int32, 0, 32) {
      for (n.outer: int32, 0, 32) {
        for (m.inner.init: int32, 0, 32) {
          C[ramp((((m.outer*32768) + (m.inner.init*1024)) + (n.outer*32)), 1, 32)] = broadcast(0f32, 32)
        }
        for (k.outer: int32, 0, 256) {
          for (m.inner: int32, 0, 32) {
            for (k.inner: int32, 0, 4) {
              let cse_var_3 = ((m.outer*32768) + (m.inner*1024))
              let cse_var_2 = (k.outer*4)
              let cse_var_1 = (cse_var_3 + (n.outer*32))
              C[ramp(cse_var_1, 1, 32)] = (C[ramp(cse_var_1: int32, 1, 32)] + (broadcast(A[((cse_var_3: int32 + cse_var_2: int32) + k.inner)], 32)*packedB_1[(((n.outer*1024) + cse_var_2) + k.inner)]))
            }
          }
        }
      }
    }
  }
}

我们主要关注一下应用Array Packing之前对B的访问方式以及使用了Array Packing之后对B的访问方式。我们之前获得的TIR的伪代码表示为：

for m_o in range(0, M, T_m):
  for n_o in range(0, N, T_n):
    for k_o in range(0, K, T_k):
      for m_i in range(m_o, m_o + T_m):
        for k_i in range(k_o, k_o + T_k):
          for n_i in range(n_o, n_o + T_n):
            C[m_i][n_i] += A[m_i][k_i] * B[k_i][n_i]

这个地方B的数据排布方式为 $[K][N]$ ，我们访问B[k_i][n_i]时需要跨维度N进行访问，跨度和N的大小即1024是相关的。由于Array Packing使得B的数据排布从 $[K][N]$ 变成 $[N/bn][K][bn]$ ，在TIR中对应了（no, ko, ki, ni) 的顺序，现在每一个小块计算时对B的数据访问一定是连续按行访问的，这就实现了我们想要的效果。

其实细心点的朋友可以发现在分块之后A虽然是按行访问的，但实际上也会跨K维度，跨度和K的大小即1024是相关的。我们为什么没有对A进行Pack呢？大家可以思考一下，接下来在Auto Schedule的对Micro Kernel汇编代码的简要分析中给出了答案。

0x4.5 Write cache for blocks（为写操作数据块创建连续内存缓存）¶

分块后，程序将结果逐块写入C，访问模式不是顺序的。所以我们可以使用一个顺序缓存数组来保存块结果并在所有块的结果准备好时写入 C。操作也比较简单，在上一节的代码基础上加一行：

# Allocate write cache
CC = s.cache_write(C, "global")

测试一下结果：

TVM Without Tune GFLOPS: 42.88957971622241

可以看到性能进一步提升了，我们看一下TIR的变化：

@main = primfn(A_1: handle, B_1: handle, C_1: handle) -> ()
  attr = {"from_legacy_te_schedule": True, "global_symbol": "main", "tir.noalias": True}
  buffers = {A: Buffer(A_2: Pointer(float32), float32, [1048576], []),
             B: Buffer(B_2: Pointer(float32), float32, [1048576], []),
             C: Buffer(C_2: Pointer(float32), float32, [1048576], [])}
  buffer_map = {A_1: A, B_1: B, C_1: C} {
  allocate(packedB: Pointer(global float32x32), float32x32, [32768]), storage_scope = global;
  allocate(C.global: Pointer(global float32), float32, [1024]), storage_scope = global {
    for (bigN: int32, 0, 32) "parallel" {
      for (k: int32, 0, 1024) {
        packedB_1: Buffer(packedB, float32x32, [32768], [])[((bigN*1024) + k)] = B[ramp(((k*1024) + (bigN*32)), 1, 32)]
      }
    }
    for (m.outer: int32, 0, 32) {
      for (n.outer: int32, 0, 32) {
        for (m.c.init: int32, 0, 32) {
          C.global_1: Buffer(C.global, float32, [1024], [])[ramp((m.c.init*32), 1, 32)] = broadcast(0f32, 32)
        }
        for (k.outer: int32, 0, 256) {
          for (m.c: int32, 0, 32) {
            let cse_var_4 = (k.outer*4)
            let cse_var_3 = (m.c*32)
            let cse_var_2 = ((n.outer*1024) + cse_var_4)
            let cse_var_1 = (((m.outer*32768) + (m.c*1024)) + cse_var_4: int32)
             {
              C.global_1[ramp(cse_var_3, 1, 32)] = (C.global_1[ramp(cse_var_3: int32, 1, 32)] + (broadcast(A[cse_var_1: int32], 32)*packedB_1[cse_var_2: int32]))
              C.global_1[ramp(cse_var_3, 1, 32)] = (C.global_1[ramp(cse_var_3, 1, 32)] + (broadcast(A[(cse_var_1 + 1)], 32)*packedB_1[(cse_var_2 + 1)]))
              C.global_1[ramp(cse_var_3, 1, 32)] = (C.global_1[ramp(cse_var_3, 1, 32)] + (broadcast(A[(cse_var_1 + 2)], 32)*packedB_1[(cse_var_2 + 2)]))
              C.global_1[ramp(cse_var_3, 1, 32)] = (C.global_1[ramp(cse_var_3, 1, 32)] + (broadcast(A[(cse_var_1 + 3)], 32)*packedB_1[(cse_var_2 + 3)]))
            }
          }
        }
        for (m.inner: int32, 0, 32) {
          for (n.inner: int32, 0, 32) {
            C[((((m.outer*32768) + (m.inner*1024)) + (n.outer*32)) + n.inner)] = C.global_1[((m.inner*32) + n.inner)]
          }
        }
      }
    }
  }
}

一个Block的结果被一个一维的顺序结果记录下来，然后在一个块计算完成后统一从这个数组中把结果取出来写入C，避免之前因为写入C不连续导致的Cache Miss。

并行和多核有关，这篇文章只关注单核我就不介绍了，感兴趣的可以看TVM的教程。

0x4.6 小结¶

接下来我们画一张图来展示目前使用了哪些优化，以及使用上这些优化之后相比于实测的浮点峰值已经达到了什么水平。

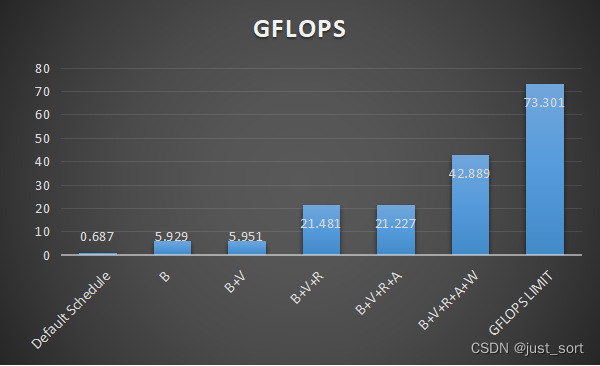
目前用到的优化和浮点峰值的对比

上面图表中的B，V，R，A，W分别是Blocking，Vectorize，Reorder，Array Packing以及Write Cache的缩写。可以看到基于这些Schedule优化，我们的性能可以来到浮点峰值的58.5%左右。

0x5. Optimizing Operators with Schedule Templates and AutoTVM 教程讲解。¶

我们这里直接跑一下官方的tune代码看看FLOPS就好，tune的配置和文档中完全一致：https://github.com/BBuf/tvm_mlir_learn/blob/main/optimize_gemm/optimize_matmul_in_gemm/tvm_autotvm_tune.py 。

其实我们从这个脚本可以发现，AutoTVM还是需要我们自己手工指定搜哪些Schedule模板从而确定搜索空间（https://github.com/BBuf/tvm_mlir_learn/blob/main/optimize_gemm/optimize_matmul_in_gemm/tvm_autotvm_tune.py#L28-L72），还是比较麻烦的，特别是对于没有调优经验的用户。后面Ansor也就是Auto Schedule将这一限制彻底放开，用户不再需要手动指定搜索参数。无论是AutoTVM还是Auto Scheduling都会给我一个搜索出的类似的结果，通过查看TIR，我们都可以了解到最终搜索出的性能更优的Schedule是什么样子。

另外AutoTVM的搜索时间也需要比较久，在服务器上卡了很久都没跑完，放弃了。所以这里直接跳过测试AutoTVM搜索出的结果，直接看TVM的下一代搜索方案Auto Scheduling的结果好了。

AutoTVM：好像不少人认为Ansor是AutoTVM的下一代，所以现在AutoTVM是不是不那么常用了？了解的小伙伴可以解答一下。

0x6. Optimizing Operators with Auto-Scheduling 教程讲解。¶

使用Auto-Scheduling来搜索Schedule不需要我们手动指定搜索空间，它会自动基于我们的默认Schedule产生更大的Schedule搜索空间并更加高效的进行搜索。在教程的基础改一改可以得到下面这个脚本：https://github.com/BBuf/tvm_mlir_learn/blob/main/optimize_gemm/optimize_matmul_in_gemm/tvm_autoschedule_tune.py 。执行python3 tvm_autoschedule_tune.py float32 tune 进行搜索并使用性能最好的Schedule进行测试。大约20分钟搜好了，获得的GFLOPS为：

TVM autoscheduler tuned GFLOPS: 62.646

和之前的优化做一个比较，如下图所示：

基于Ansor得到的最好结果，搜索了20分钟

现在基于Ansor的最好结果，达到了浮点峰值的85.5%，感觉是相当不错的结果了，相比于默认Schedule的Naive程序性能提升了91倍。

接下来我们从这个TIR出发来探索一下为什么Ansor搜索出的方案比0x4节的手工调优的方案性能更优？

首先打印一下基于Ansor搜索出的Schedule对应的TIR：

@main = primfn(A_1: handle, B_1: handle, C_1: handle) -> ()
  attr = {"from_legacy_te_schedule": True, "global_symbol": "main", "tir.noalias": True}
  buffers = {A: Buffer(A_2: Pointer(float32), float32, [1048576], []),
             B: Buffer(B_2: Pointer(float32), float32, [1048576], []),
             C: Buffer(C_2: Pointer(float32), float32, [1048576], [])}
  buffer_map = {A_1: A, B_1: B, C_1: C} {
  allocate(auto_scheduler_layout_transform: Pointer(global float32), float32, [1048576]), storage_scope = global {
    for (ax0.ax1.fused.ax2.fused: int32, 0, 16) "parallel" {
      for (ax4: int32, 0, 16) {
        for (ax5: int32, 0, 2) {
          for (ax6: int32, 0, 64) {
            for (ax7: int32, 0, 32) {
              auto_scheduler_layout_transform_1: Buffer(auto_scheduler_layout_transform, float32, [1048576], [])[(((((ax0.ax1.fused.ax2.fused*65536) + (ax4*4096)) + (ax5*2048)) + (ax6*32)) + ax7)] = B[(((((ax4*65536) + (ax6*1024)) + (ax0.ax1.fused.ax2.fused*64)) + (ax5*32)) + ax7)]
            }
          }
        }
      }
    }
    for (i.outer.outer.j.outer.outer.fused: int32, 0, 8) "parallel" {
      allocate(C.local: Pointer(local float32), float32, [2048]), storage_scope = local;
      for (i.outer.inner: int32, 0, 32) {
        for (j.outer.inner: int32, 0, 2) {
          C.local_1: Buffer(C.local, float32, [2048], [], scope="local")[ramp(0, 1, 32)] = broadcast(0f32, 32)
          C.local_1[ramp(64, 1, 32)] = broadcast(0f32, 32)
          // 省略了对C.local_1其它部分的初始化
          for (k.outer: int32, 0, 16) {
            for (i.c.outer.inner: int32, 0, 16) {
              for (j.c.outer.inner: int32, 0, 2) {
                for (k.inner: int32, 0, 64) {
                  let cse_var_4 = ((i.c.outer.inner*128) + (j.c.outer.inner*32))
                  let cse_var_3 = (cse_var_4 + 64)
                  let cse_var_2 = ((((i.outer.inner*32768) + (i.c.outer.inner*2048)) + (k.outer*64)) + k.inner)
                  let cse_var_1 = (((((i.outer.outer.j.outer.outer.fused*131072) + (j.outer.inner*65536)) + (k.outer*4096)) + (j.c.outer.inner*2048)) + (k.inner*32))
                   {
                    C.local_1[ramp(cse_var_4, 1, 32)] = (C.local_1[ramp(cse_var_4: int32, 1, 32)] + (broadcast(A[cse_var_2: int32], 32)*auto_scheduler_layout_transform_1[ramp(cse_var_1: int32, 1, 32)]))
                    C.local_1[ramp(cse_var_3, 1, 32)] = (C.local_1[ramp(cse_var_3: int32, 1, 32)] + (broadcast(A[(cse_var_2 + 1024)], 32)*auto_scheduler_layout_transform_1[ramp(cse_var_1, 1, 32)]))
                  }
                }
              }
            }
          }
          for (i.inner: int32, 0, 32) {
            for (j.inner: int32, 0, 64) {
              C[(((((i.outer.inner*32768) + (i.inner*1024)) + (i.outer.outer.j.outer.outer.fused*128)) + (j.outer.inner*64)) + j.inner)] = C.local_1[((i.inner*64) + j.inner)]
            }
          }
        }
      }
    }
  }
}

可以看到相比于0x4节手动指定Schedule的 $32\times 32$ 分块，这里搜出来的分块大小是 $32\times 64$ ，C.local和C.local_1做的就是写缓存Schedule的优化。同样矩阵B被Pack到了auto_scheduler_layout_transform里。从for (i.outer.outer.j.outer.outer.fused: int32, 0, 8) "parallel" 可以判断矩阵C被分成了8个小块，每个小块用单独的线程计算，我们可以计算出每个小块的大小为 $128\times 128$ 。

从这两代码：

for (i.outer.inner: int32, 0, 32) {
        for (j.outer.inner: int32, 0, 2)

可以看到，8个小块中的每一个块又被分成 $4\times 64=256$ 个 $32\times 2$ 的小小块。假如k维度没有被Blocking的话，这个 $32\times 2$ 的C的小小块应该是 $32\times 1024$ （A的一个小小块）以及 $1024\times 2$ （B的一个小小块）的矩阵乘。然后从搜索结果可以看到这里对k又做了Blocking，所以A的小小块又被拆成了 $1024/16=64$ 个 $32\times 16$ 大小的小小小块，同理B的小小块也被拆成了 $1024/16=64$ 个 $16\times 2$ 大小的小小小块。

从理论上来说，最内三层循环对应的C的小小块和A，B的小小小块可以放到L1 Cache，再往外看一个循环C的小块以及A，B的小小块可以放到更大的L2 Cache，如果搞得更夸张一点还可以尝试把A，B的小块放到L3 Cache。

综上，基于Ansor搜索的方案对Blocking做了更加精细的调整使其适应CPU的多级缓存，使得Cache Miss的概率更小，进而更加有效的提升GFLOPS。

上面提到了我们在这个基于Ansor搜索的程序中，最终的子任务就是完成 $32\times 16$ 以及 $16\times 2$ 的小矩阵的Kernel了。不妨研究一下从TIR生成的汇编代码：

.LBB3_25:
        vbroadcastss    -4100(%rdi,%rbp,4), %ymm8
        vmovaps -128(%rdx), %ymm9
        vmovaps -96(%rdx), %ymm10
        vmovaps -64(%rdx), %ymm11
        vmovaps -32(%rdx), %ymm12
        vmovaps %ymm7, %ymm13
        vfmadd231ps     %ymm12, %ymm8, %ymm13
        vfmadd231ps     %ymm11, %ymm8, %ymm6
        vfmadd231ps     %ymm9, %ymm8, %ymm4
        vfmadd231ps     %ymm8, %ymm10, %ymm5
        vbroadcastss    -4(%rdi,%rbp,4), %ymm7
        vfmadd231ps     %ymm12, %ymm7, %ymm3
        vfmadd231ps     %ymm11, %ymm7, %ymm2
        vfmadd231ps     %ymm9, %ymm7, %ymm0
        vfmadd231ps     %ymm10, %ymm7, %ymm1
        vbroadcastss    -4096(%rdi,%rbp,4), %ymm7
        vmovaps 96(%rdx), %ymm8
        vmovaps 64(%rdx), %ymm9
        vmovaps (%rdx), %ymm10
        vmovaps 32(%rdx), %ymm11
        vfmadd231ps     %ymm11, %ymm7, %ymm5
        vfmadd231ps     %ymm10, %ymm7, %ymm4
        vfmadd231ps     %ymm9, %ymm7, %ymm6
        vfmadd213ps     %ymm13, %ymm8, %ymm7
        vbroadcastss    (%rdi,%rbp,4), %ymm12
        vfmadd231ps     %ymm11, %ymm12, %ymm1
        vfmadd231ps     %ymm10, %ymm12, %ymm0
        vfmadd231ps     %ymm9, %ymm12, %ymm2
        vfmadd231ps     %ymm8, %ymm12, %ymm3
        addq    $2, %rbp
        addq    $256, %rdx
        cmpq    $64, %rbp
        jne     .LBB3_25

在一个C小块（ $32\times 2$ ）的计算中，C的所有数据驻寄存器ymm0~ymm7。k从0-16循环，将b（1x2）的值加载到了ymm8中，然后将a（1x32）个值加载到了ymm9，ymm10，ymm11，ymm12中并和ymm8乘加完成计算。另外，我们可以看到数组B的元素是连续存放的，而数组A的元素跨度为4096：vbroadcastss -4096(%rdi,%rbp,4), %ymm7 ，代表A没有做任何Pack。在这个小块里面，数组A完全可以放到寄存器中是否做Pack也对性能没什么影响。

0x7. 总结¶

最近在整理一些编译器方面的基础知识翻译，回顾了一下TVM的Schedule然后想起自己1年前做的一些GEMM相关的实验和探索没做什么总结。所以基于TVM的三个教程也即TVM的三代优化来做对之前的学习做一个简单的总结，在本篇文章中我原创的内容主要集中在对各个Schedule的单独详解以及引入了TIR的伪代码描述帮助读者更好的理解TVM Schedule。还有深入解读了Blocking技术以及Auto Schedule搜出的高性能程序，简要分析了micro Kernel的汇编。另外我制作了一个控制Schedule变量进行测试得到的GFLOPS柱状图，方便大家对比各代优化的效果。

0x8. 参考资料¶

本文总阅读量次