CVPR 2021 如何理解对比学习中的温度系数？

1. 论文信息¶

标题：Understanding the Behaviour of Contrastive Loss

作者：Feng Wang, Huaping Liu

原文链接：https://openaccess.thecvf.com/content/CVPR2021/papers/Wang_Understanding_the_Behaviour_of_Contrastive_Loss_CVPR_2021_paper.pdf#:~:text=the%20%EE%80%80contrastive%EE%80%81%20%EE%80%80loss%EE%80%81%20is%20a%20hardness-aware%20%EE%80%80loss%EE%80%81%20function,Specif-ically%2C%20%EE%80%80contrastive%EE%80%81%20%EE%80%80loss%EE%80%81%20with%20small%20temperature%20tends%20

2. 引入¶

无监督的对比学习可以引导模型以学习到很多关于数据集的信息。由于无需任何注释或标签，可以进行自监督，所以可以比较好地学习到图像的各种视觉表征。经过大量研究人员的关注，无监督对比学习已经取得了显著的成功，但对对比损失的机理研究较少。

大部分CVPR的论文侧重于各种网络模块的设计和各种SOTA来说明模块设计的有效性，而是对比学习的损失函数中的temperature参数这个点进行非常深入的解读。各种实验的设定是服务于偏数学理论的论述的。对于我们理解对比学习的损失函数非常有帮助。

其实本文很大程度上是延续了ICML 2021:Understanding Contrastive Representation Learning through Alignment and Uniformity on the Hyperspher 这份工作的思路。

可以参考：

https://blog.csdn.net/pitaojun/article/details/108869569

概括来讲，ICML这份工作实际上对于对比学习的实质，是这样阐释的：contrastive loss 具有两种性质：（1）alignment 用来衡量正例对样本间的近似程度。（2）uniformity 衡量规整后的特征在unit 超球体上的分布的均匀性。并提出了衡量两种性质的metric，并且揭示了对这两个指标的训练学到的特征在下游任务上表现更好。

其实两个性质的优化目标很直观：

Alignment 让相同的样本的特征尽可能相似。
Uniformity使得特征的分布保持尽可能多的信息。

在这篇论文中，我们集中在无监督对比损失的行为的理解。我们将表明，对比损失是一个hard-感知的损失函数，温度t控制硬负样品的惩罚强度。先前的研究表明，一致性是对比学习的一个关键特性。我们建立了均一性与温度t之间的关系。论文将证明，均一性有助于对比学习学习可分离特征。

这Alignment和Uniformity这两个metric代码也非常简单：

# bsz : batch size (number of positive pairs)
# d : latent dim
# x : Tensor, shape=[bsz, d]
# latents for one side of positive pairs
# y : Tensor, shape=[bsz, d]
# latents for the other side of positive pairs
def align_loss(x, y, alpha=2):
   return (x - y).norm(p=2, dim=1).pow(alpha).mean()

def uniform_loss(x, t=2):
   return torch.pdist(x, p=2).pow(2).mul(-t).exp().mean().log()

对比学习方法有一个共同的loss function设计，就是一个与温度相关的feature similarity的softmax函数，以帮助区分正样本和负样本。这种形式的loss function无疑是无监督对比学习成功的重要因素。在本文中，作者着重分析了该损失函数的性质，同时分析以温度这种形式的重要影响。按作者的话说，对比损失是一个hardness-aware 的loss。温度对hard negative samples的惩罚度有一定的控制作用。具体而言，温度较低的对比损失对最hard的negative samples惩罚更大，使每个样品的局部结构更分散，嵌入分布可能更均匀。另一方面，大温度下的对比loss对hard的negative samples的敏感性较低，当温度接近无穷大时，对硬度的敏感性消失。硬度感知特性对于基于softmax的对比损失的成功非常重要，通过明确的hardness-aware策略，这种非常简单的对比损失形式非常有效。

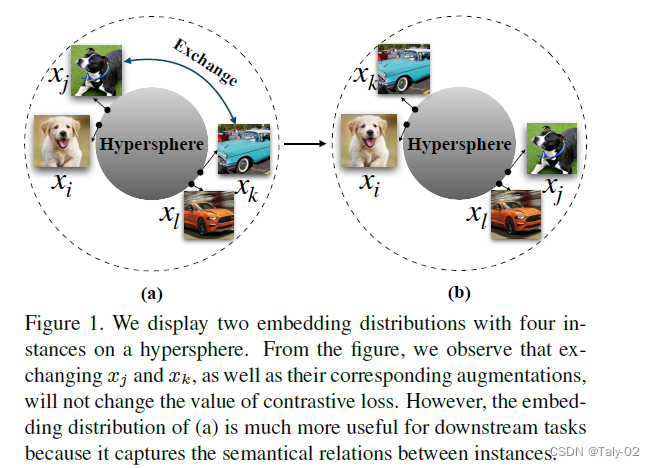
上图在一个超球上展示了两个包含四个实例的embeddings分布。从图中我们可以看出，交换 $x_{i}$ 和 $x_{j}$ ，以及它们的相应的增加并不会改变对比损失的价值。然而，(a)的embeddings分布对于下游任务更有用，因为它捕获了实例之间的语义关系。结合上图来看，其实总结温度系数的作用，就是来是调节对困难样本的关注程度：越小的温度系数越关注于将本样本和最相似的其他样本分开。而对比损失存在一个Uniformity-Tolerance Dilemma。小温度系数更关注于将与本样本相似的困难样本分开，因此往往可以得到更均匀的表示。然而困难样本往往是与本样本相似程度较高的，例如同一个类别的不同实例，即有很多困难负样本其实是潜在的正样本。过分强迫与困难样本分开会破坏学到的潜在语义结构。

4. 方法¶

首先回顾一下我们非常熟悉的对比学习的损失函数形式：

$\mathcal{L}\left(x_i\right)=-\log \left[\frac{\exp \left(s_{i, i} / \tau\right)}{\sum_{k \neq i} \exp \left(s_{i, k} / \tau\right)+\exp \left(s_{i, i} / \tau\right)}\right]$

作者为了方便进一步的阐释，对这个形式做出了一定程度的简化：

$\mathcal{L}_{\text {simple }}\left(x_i\right)=-s_{i, i}+\lambda \sum_{i \neq j} s_{i, j}$

对上式进行求导可以得到：

$\frac{\partial \mathcal{L}\left(x_i\right)}{\partial s_{i, i}}=-\frac{1}{\tau} \sum_{k \neq i} P_{i, k}$

$\frac{\partial \mathcal{L}\left(x_i\right)}{\partial s_{i, j}}=\frac{1}{\tau} P_{i, j}$

$P_{i, j}=\frac{\exp \left(s_{i, j} / \tau\right)}{\sum_{k \neq i} \exp \left(s_{i, k} / \tau\right)+\exp \left(s_{i, i} / \tau\right)}$

所以对于不同的负样本，其实反向传播的梯度和温度是成反比的，温度越低，则梯度越大；而 $s_{i,j}$ 越大（样本越难学），则梯度越大。这反映出了对比学习损失函数Hardness-aware的这一特性。

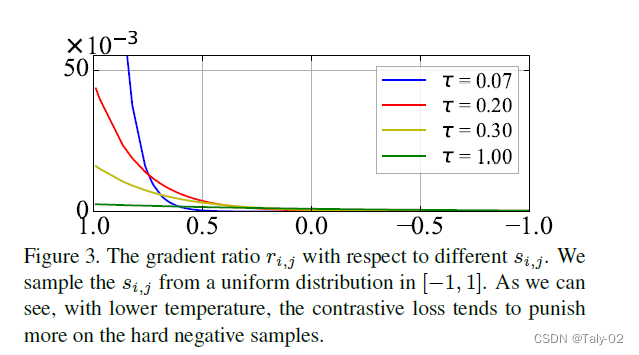
上图很好得反映了温度对于反向传播梯度的影响，展示出了Hardness-aware这一特性。

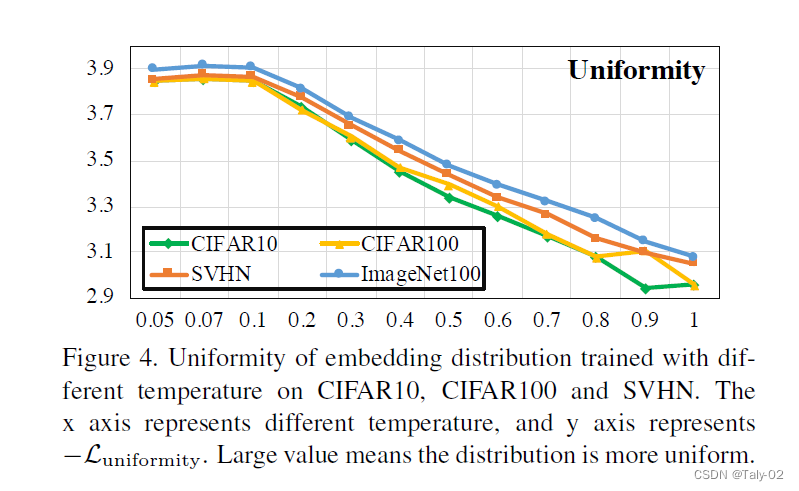
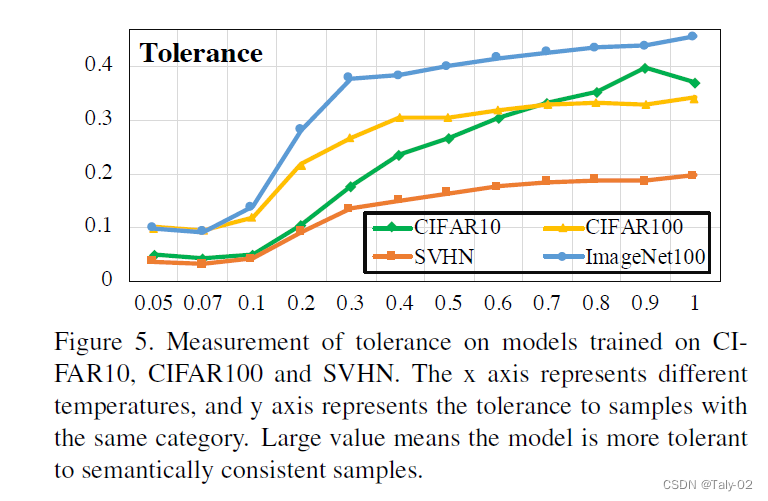
随着temperatrue的增大，tolerance这个值也在增大，说明语义相关的样本的相似度在变大。一个理想的模型，应该是局部聚集，全局均匀的，也就是tolerance要大的同时，uniformity要小。但根据上面两个图，tolerance增大时，uniformity也在增大；tolerance减小时，uniformity也在减小，这便形成了一个作者所定义的Uniformity-Tolerance Dilemma。所以对于一般的对比学习loss而言，如何选择一个合适的temporature来平衡embedding的聚集性和均匀性，是需要根据具体问题来权衡的。

因此，作者根据前人的启发，定义了一个Hard Contrastive Loss：

$\mathcal{L}_{\text {hard }}=-\log \frac{\exp \left(s_{i, i} / \tau\right)}{\sum_{s_{i, k} \geq s_\alpha^{(i)}} \exp \left(s_{i, k} / \tau\right)+\exp \left(s_{i, i} / \tau\right)}$

即通过预定义一个相似度临界点，把一部分的负样本定义为informative hard negative samples，另一部分定义为uninformative interval，把训练过程中的梯度归类到一个区间中。

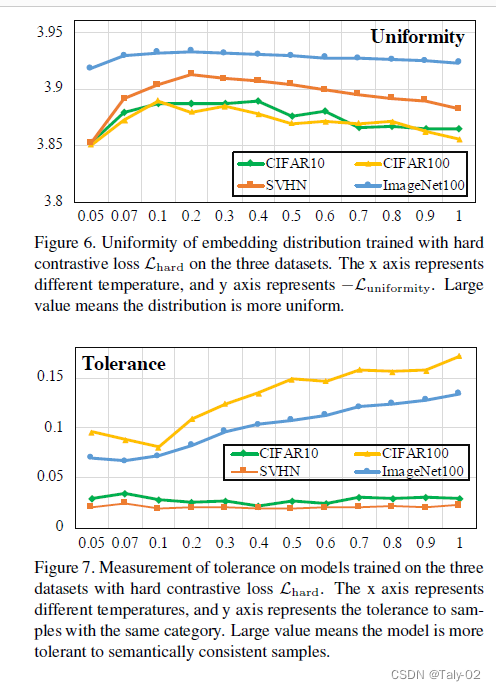
可以看到通过这种方式，模型得到的embedding既保持均匀，又能局部聚集，从而保留一定潜在语义结构，破解上一节所说的Uniformity-Tolerance Dilemma问题。

5. 结论¶

在本篇论文中，作者从temperature这个参数入手，从理论和实验的角度指出Contrastive Loss是一个hardness-aware的损失函数，而temperature在控制embedding分布中扮演着重要作用，并由此提出一种Uniformity-Tolerance Dilemma问题。

本文总阅读量次