前言¶

在阅读DarkNet源码的时候发现作者定义了大量从古至今流行的损失函数，本着科普的态度我打算做一个全面的总结，所以就有了这篇文章。

激活函数有什么用？¶

提到激活函数，最想问的一个问题肯定是它是干什么用的？激活函数的主要作用是提供网络的非线性表达建模能力，想象一下如果没有激活函数，那么神经网络只能表达线性映射，此刻即便是有再多的隐藏层，其整个网络和单层的神经网络都是等价的。因此正式由于激活函数的存在，深度神经网络才具有了强大的非线性学习能力。接下来我们就来盘点一下当前有哪些流行的激活函数吧，这是一件非常有意义的事，希望你能接着读下去。

1. Sigmoid激活函数¶

函数表达式： $f(x)=\frac{1}{1+e^{-x}}$
函数图像：

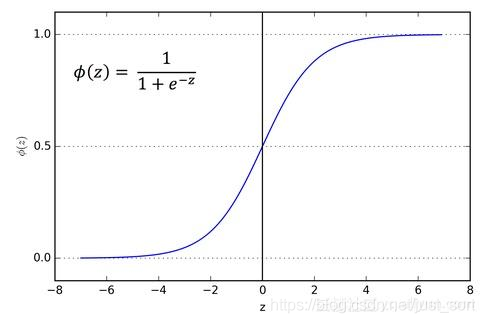
Sigmoid激活函数

导数： $f'(x)=f(x)(1-f(x))$
优点：Sigmoid激活函数是应用范围最广的一类激活函数，具有指数形状，它在物理意义上最为接近生物神经元。另外，Sigmoid的输出是(0,1)，具有很好的性质，可以被表示为概率或者用于输入的归一化等。可以看出，Sigmoid函数连续，光滑，严格单调，以(0,0.5)中心对称，是一个非常良好的阈值函数。当x趋近负无穷时，y趋近于0；x趋近于正无穷时，y趋近于1；x=0时，y=0.5。当然，在x超出[-6,6]的范围后，函数值基本上没有变化，值非常接近，在应用中一般不考虑。Sigmoid函数的导数是其本身的函数，即f′(x)=f(x)(1−f(x))，计算非常方便，也非常节省计算时间。
缺点：Sigmoid最明显的缺点就是饱和性。从曲线图中看到，其两侧的导数逐渐趋近于0，即： $\lim_{x->\infty}f'(x)0$ 。我们将具有这种性质的激活函数叫作软饱和激活函数。具体的，饱和又可分为左饱和与右饱和。与软饱和对应的是硬饱和, 即f′(x)=0，当|x|>c，其中c为常数。sigmoid 的软饱和性，使得深度神经网络在二三十年里一直难以有效的训练，是阻碍神经网络发展的重要原因。另外，Sigmoid函数的输出均大于0，使得输出不是0均值，这称为偏移现象，这会导致后一层的神经元将得到上一层输出的非0均值的信号作为输入。

2. TanH¶

函数表达式： $f(x)=\frac{1-e^{-2x}}{1+e^{-2x}}$
函数图像：

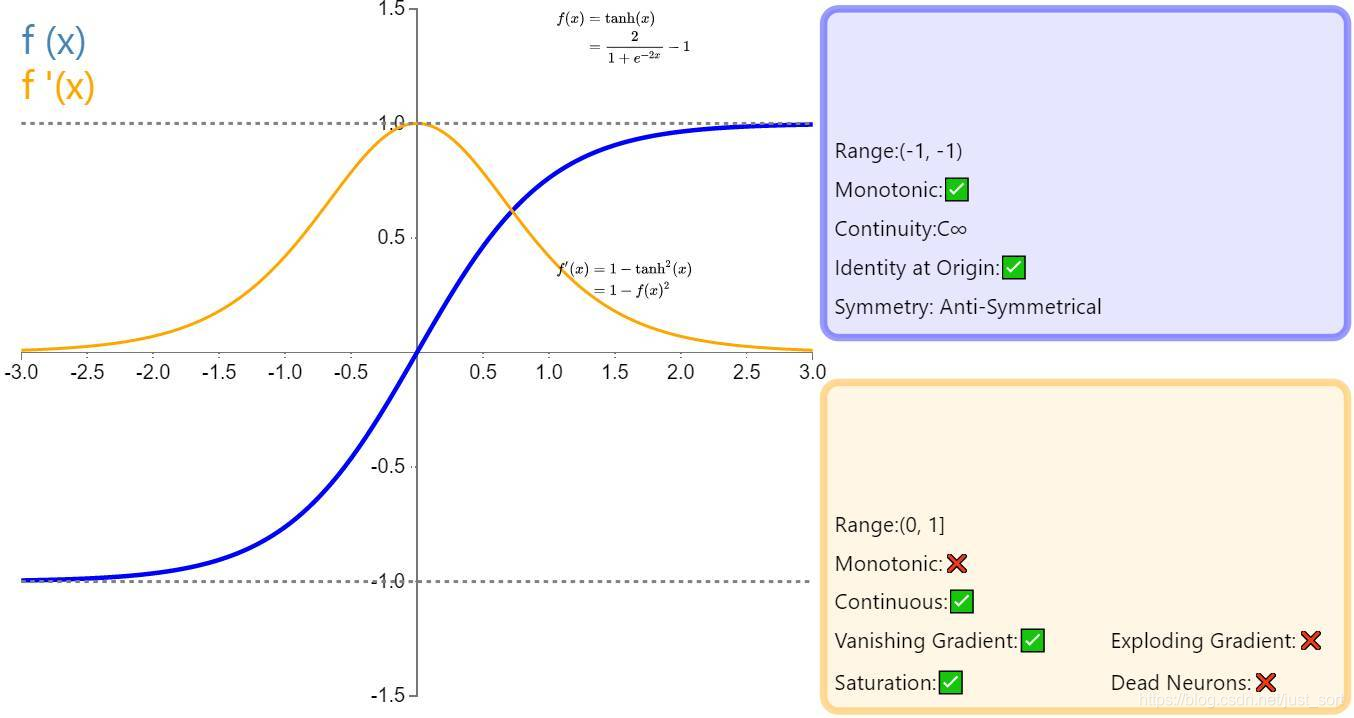
Tanh激活函数和它的导数

导数： $f'(x)=1-f(x)^2$
优点：与Sigmoid相比，它的输出均值是0，使得其收敛速度要比Sigmoid快，减少迭代次数。
缺点：该导数在正负饱和区的梯度都会接近于0值(仍然具有软饱和性)，会造成梯度消失。还有其更复杂的幂运算。

3. ReLU¶

函数表达式： $f(x)=max(0,x)$
函数图像：

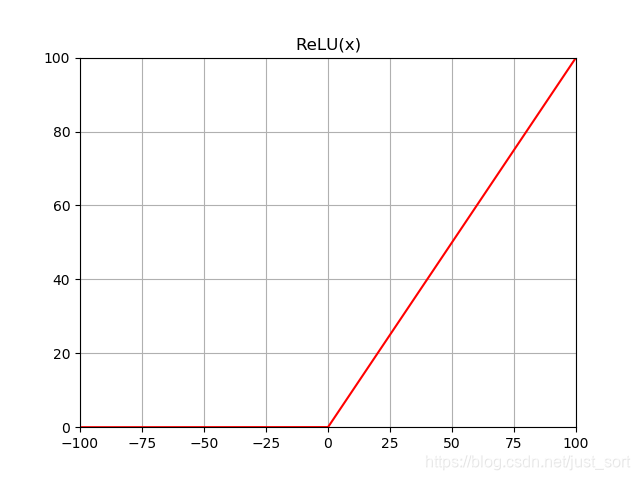
ReLU激活函数

导数：当 $x>0$ 时 $f'(x)=1$ ，当 $x<0$ 时 $f'(x)=0$
优点：ReLU的全称是Rectified Linear Units，是一种AlexNet时期才出现的激活函数。可以看到，当x<0时，ReLU硬饱和，而当x>0时，则不存在饱和问题。所以，ReLU 能够在x>0时保持梯度不衰减，从而缓解梯度消失问题。这让我们能够直接以监督的方式训练深度神经网络，而无需依赖无监督的逐层预训练。
缺点：随着训练的推进，部分输入会落入硬饱和区，导致对应权重无法更新。这种现象被称为“神经元死亡”。与Sigmoid类似，ReLU的输出均值也大于0，偏移现象和神经元死亡会共同影响网络的收敛性。

4. Leaky ReLU & PReLU¶

函数表达式和导数：

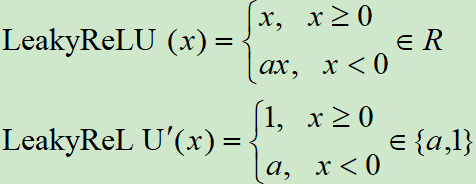
Leaky ReLU

函数图像：

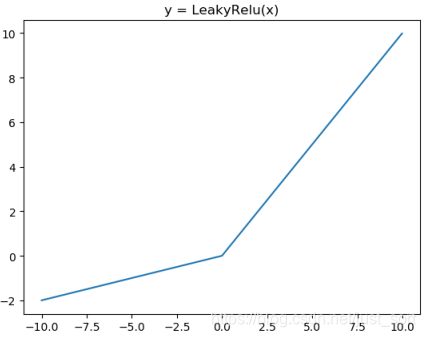
Leaky ReLU激活函数

特点：为了改善ReLU在 $x<0$ 时梯度为 $0$ 造成Dead ReLU，提出了Leaky ReLU使得这一问题得到了缓解。例如在我们耳熟能详的YOLOV3网络中就使用了Leaky ReLU这一激活函数，一般 $a$ 取 $0.25$ 。另外PReLU就是将Leaky ReLU公式里面的 $a$ 当成可学习参数参与到网络训练中。

5. ReLU6¶

函数表达式： $f(x)=min(max(0,x),6)$
特点：ReLU6就是普通的ReLU但是限制最大输出值为6（对输出值做clip），这是为了在移动端设备float16的低精度的时候，也能有很好的数值分辨率，如果对ReLU的激活范围不加限制，输出范围为0到正无穷，如果激活值非常大，分布在一个很大的范围内，则低精度的float16无法很好地精确描述如此大范围的数值，带来精度损失。

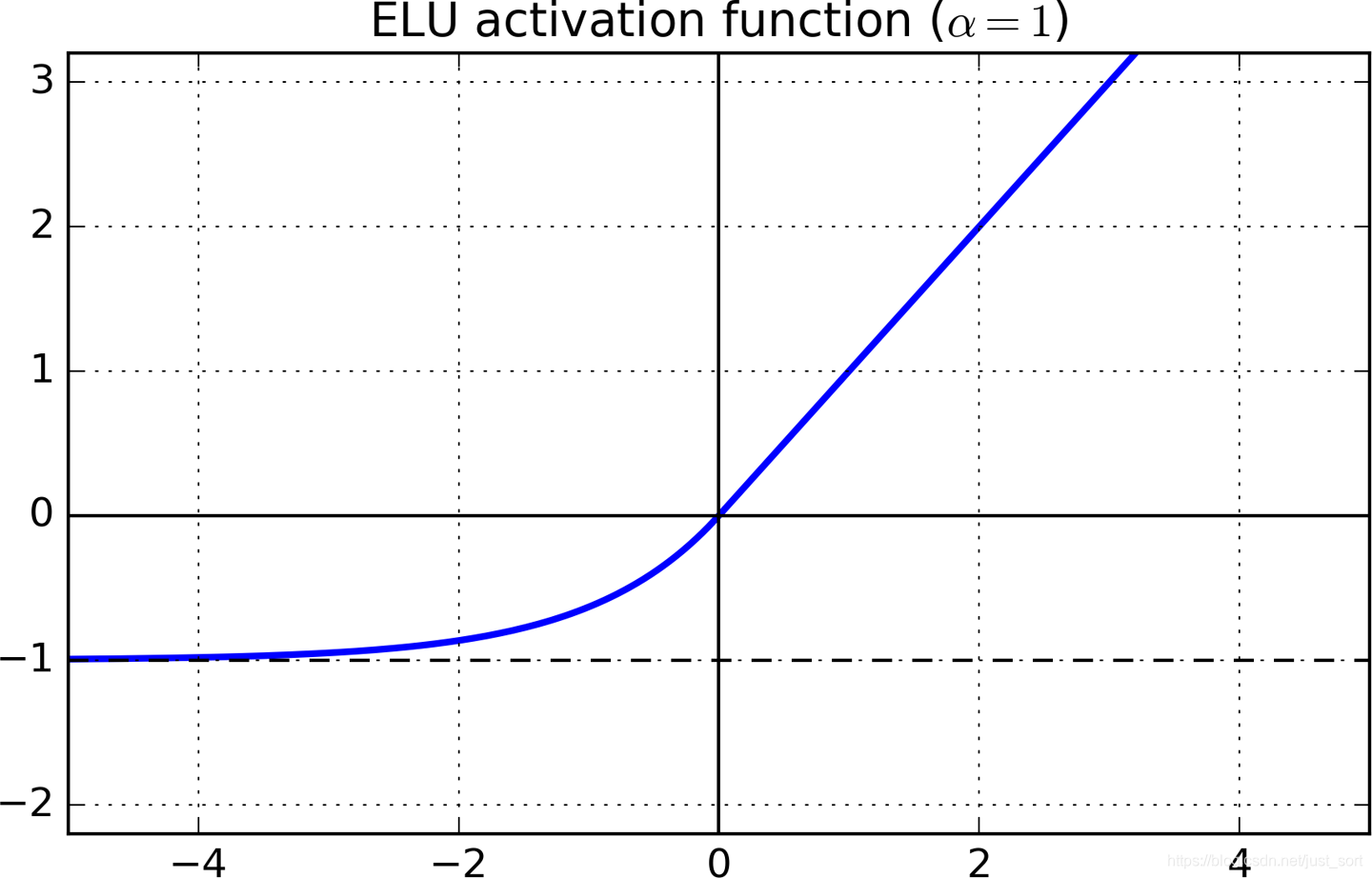
6. ELU¶

函数表达式：

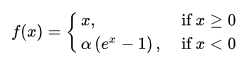
ELU表达式

函数图像：

ELU激活函数

导数：当 $x>=0$ 时， $f'(x)=1$ ，当 $x<0$ 时， $f'(x)=\alpha e^x$ 。
特点：融合了sigmoid和ReLU，左侧具有软饱和性，右侧无饱和性。右侧线性部分使得ELU能够缓解梯度消失，而左侧软饱能够让ELU对输入变化或噪声更鲁棒。ELU的输出均值接近于零，所以收敛速度更快。在 ImageNet上，不加Batch Normalization 30层以上的ReLU网络会无法收敛，PReLU网络在MSRA的Fan-in （caffe ）初始化下会发散，而 ELU 网络在Fan-in/Fan-out下都能收敛。关于Fan-in/Fan-out初始化请看附录的参考2链接。

7. SoftSign¶

函数表达式： $f(x)=\frac{x}{1+|x|}$
函数图像：

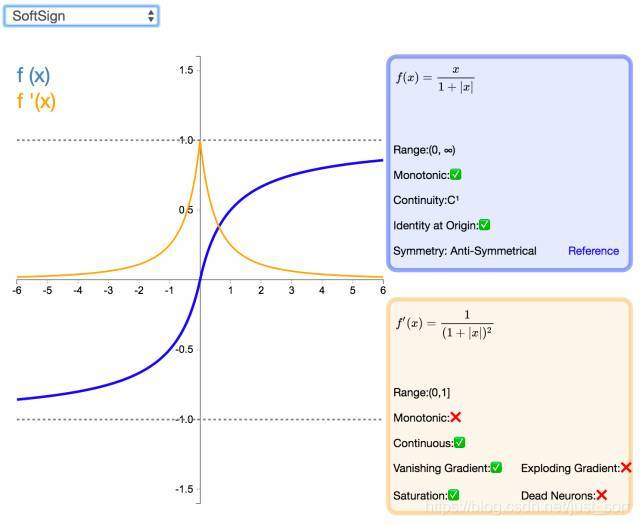
Softsign激活函数和它的导数

导数：图中已经求出。
特点：Softsign是tanh激活函数的另一个替代选择，从图中可以看到它和tanh的曲线极其相似，不过相比于tanh，Softsign的曲线更平坦，导数下降的更慢一点，这个特性使得它可以缓解梯度消失问题，可以更高效的学习。

8. SoftPlus¶

函数表达式： $f(x)=ln(1+e^x)$
函数图像：

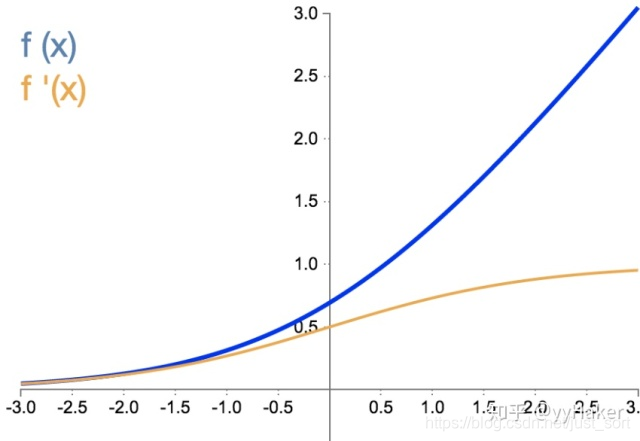
SoftPlus激活函数及导数

函数导数：SoftPlus激活函数的导数恰好就是sigmoid激活函数，即 $f'(x)=sigmoid(x)$ 。
优点：SoftPlus可以作为ReLu的一个不错的替代选择，可以看到与ReLU不同的是，SoftPlus的导数是连续的、非零的、无处不在的，这一特性可以防止出现ReLU中的“神经元死亡”现象。
缺点：SoftPlus是不对称的，不以0为中心，存在偏移现象；而且，由于其导数常常小于1，也可能会出现梯度消失的问题。

9. SELU¶

函数表达式： $SELU(x)=\lambda * ELU(x)$ ，也即是：

$f(x)=\lambda \begin{cases} \alpha(e^x-1) & x \le 0 \\ x & x>0 \end{cases}$

特点：这个激活函数来自论文：https://arxiv.org/abs/1706.02515 。而这篇论文就是提出了这一激活函数，然后论文写了93页公式来证明只需要把激活函数换成SELU就能使得输入在经过一定层数之后变成固定的分布。。而这个函数实际上就是在ELU激活函数的基础上乘以了一个 $\lambda$ ，但需要注意的是这个 $\lambda$ 是大于1的。
更详细的讨论可以见这里：https://www.zhihu.com/question/60910412

10. Swish¶

函数表达式： $f(x)=x*sigmoid(x)$ ，其中 $\beta$ 是个常数或可训练的参数.Swish 具备无上界有下界、平滑、非单调的特性。
函数图像：

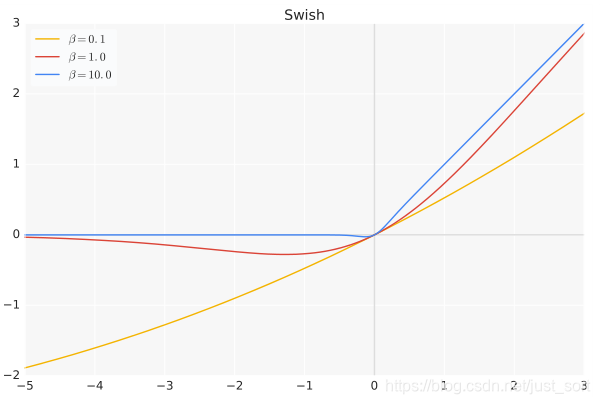
Swish激活函数

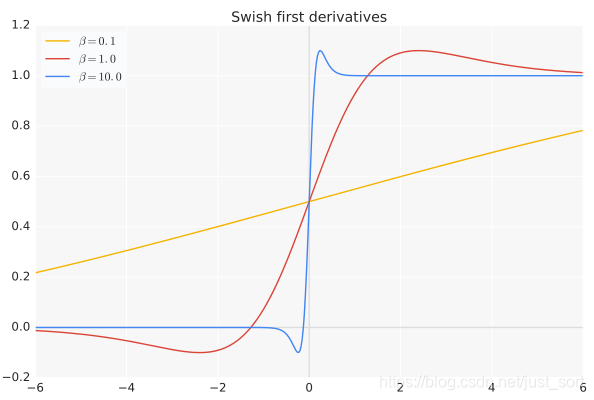
Swish激活函数导数

特点：Swish 在深层模型上的效果优于 ReLU。例如，仅仅使用 Swish 单元替换 ReLU 就能把 Mobile NASNetA 在 ImageNet 上的 top-1 分类准确率提高 0.9%，Inception-ResNet-v的分类准确率提高 0.6%。当 $\beta=0$ 时，Swish激活函数变成线性函数 $f(x)=\frac{x}{2}$ .而当 $\beta->\infty$ 时， $\delta(x)=(1+exp(-x))^{-1}$ 为0或1,这个时候Swish激活函数变成ReLU激活函数 $f(x)=2max(0,x)$ 。因此Swish激活函数可以看做是介于线性函数与ReLU函数之间的平滑函数。

11. Maxout¶

函数表达式： $f(x)=max(w_1^Tx+b_1,w_2^Tx+b_2,...,w_n^Tx+b_n)$
特点：Maxout模型实际上也是一种新型的激活函数，在前馈式神经网络中，Maxout的输出即取该层的最大值，在卷积神经网络中，一个Maxout特征图可以是由多个特征图取最值得到。 Maxout的拟合能力是非常强的，它可以拟合任意的的凸函数。但是它和Dropout一样需要人为设定一个 $k$ 值。为了便于理解，假设有一个在第 $i$ 层有 $2$ 个节点 $i+1$ 层有 $1$ 个节点构成的神经网络。即：

神经网络

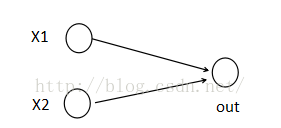
激活值 $out = f(W*X+b)$ ，其中 $f$ 是激活函数， $*$ 在这里代表內积。然后 $X=(x1,x2)^T$ , $W=(w_1,w_2)^T$ 。那么当我们对 $i+1$ 层使用Maxout（设定 $k=5$ ）然后再输出的时候，情况就发生了改变。网络就变成了：

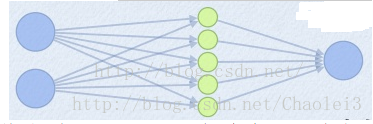
使用了Maxout后的网络

此时网络形式上就变成上面的样子，用公式表现出来就是：

$z1 = W1*X+b1$ $z2 = W2*X+b2$ $z3 = W3.X+b3$ $z4 = W4.X+b4$ $z5 = W4.X+b5$ $out = max(z1,z2,z3,z4,z5)$

也就是说第 $i+1$ 层的激活值计算了 $5$ 次，可我们明明只需要 $1$ 个激活值，那么我们该怎么办？其实上面的叙述中已经给出了答案，取这 $5$ 个的最大值来作为最终的结果。

可以看到采用Maxout的话参数个数也增加了 $k$ 倍，计算开销会增大。

12. Mish¶

函数表达式： $Mish(x)=x*tanh(ln(1+e^x))$
函数图像：

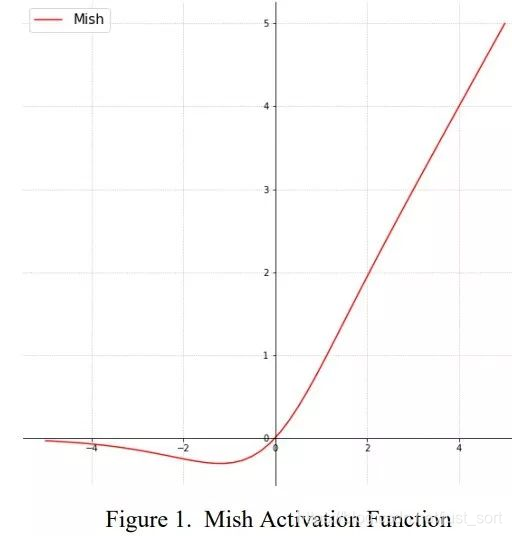
MisH激活函数

特点：这个激活函数是最新的SOTA激活函数，我还没具体使用和了解过这个激活函数，就暂时不总结这一个了。不过论文中提到，以上无边界(即正值可以达到任何高度)避免了由于封顶而导致的饱和，理论上对负值的轻微允许更好的梯度流，而不是像ReLU中那样的硬零边界，并且整个损失函数仍然保持了平滑性。
论文名为：Mish: A Self Regularized Non-Monotonic Neural Activation Function

激活函数尝试经验¶

首先使用ReLU，速度最快，然后观察模型的表现。
如果ReLU效果不是很好，可以尝试Leaky ReLU或Maxout等变种。
尝试tanh正切函数(以零点为中心,零点处梯度为1)。
在深度不是特别深的CNN中，激活函数的影响一般不会太大。
Kaggle比赛，试试Mish？

附录¶

参考1：https://www.cnblogs.com/missidiot/p/9378079.html
参考2：https://keras-cn.readthedocs.io/en/latest/other/initializations/
参考3：https://zhuanlan.zhihu.com/p/70810466
参考4：https://www.cnblogs.com/makefile/p/activation-function.html
参考5：https://www.cnblogs.com/missidiot/p/9378079.html

前言¶