分布式概率SLAM图中的增量抽象¶

0. 引言¶

对于长期SLAM任务，通过限制因子图的增长来匹配地图的空间范围，进而管理计算成本是至关重要的，同时由于最近的SLAM系统广泛关注因子图中包含语义元素的增量场景重建，因此基于因子图构建场景图具有很强的挑战性。在2022 CVPR论文"Incremental Abstraction in Distributed Probabilistic SLAM Graphs"中，作者提出了一个分布式的、基于图结构的SLAM框架，并展示了其高效性。作者对于图形处理器上的BA部分的python代码已经开源。

1. 论文信息¶

标题：Incremental Abstraction in Distributed Probabilistic SLAM Graphs

作者：Joseph Ortiz, Talfan Evans, Edgar Sucar, Andrew J. Davison

来源：2022 Computer Vision and Pattern Recognition (CVPR)

原文链接：https://arxiv.org/abs/2109.06241

代码链接：https://joeaortiz.github.io/incremental_abstraction

2. 摘要¶

场景图以紧凑和语义丰富的方式表示场景的关键组件，但在增量SLAM运行期间难以构建，因为鲁棒地识别抽象场景元素和优化不断变化的复杂图形存在挑战。我们提出了一个分布式的、基于图结构的SLAM框架，用于基于两个新颖的组件增量地构建场景图。

首先，我们提出了一个增量抽象框架，其中神经网络提出抽象的场景元素，这些元素被合并到基于特征点的单目SLAM系统的因子图中。通过优化来确认或拒绝场景元素，并递增地替换这些点，从而产生更密集、语义和紧凑的表示。第二，通过我们新的路由过程，我们使用高斯置信传播(Gaussian Belief Propagation, GBP)在图形处理器上进行分布式推理。GBP每次迭代的时间是结构无关的，我们展示了在异构因子图推断方面比直接法的速度优势。我们使用平面抽象在真实的室内数据集上运行我们的系统，并恢复具有显著压缩的主要平面。

3. 算法分析¶

如图1所示是作者提出的算法原理和定性三维重建结果，由于高斯置信传播(GBP)的每次迭代的时间是结构不可知的，因此它可以快速优化增量场景抽象中出现的稀疏结构的因子图。在图中，绿色节点为点，红色节点为平面。

图1 算法概述

如图2所示是作者使用的因子图具体结构，其中左图表示只有关键帧和点的原始因子图。中间展示网络预测关键帧3中的平面π1，点p2和p3分别位于预测的分割掩模内。同时将平面假设变量节点连同2个平面-点距离因子和一个平面预测因子一起添加到图结构中。右图表示确认平面假设，并将平面假设和点替换为刚体平面节点r1。具有虚线边界的因子连接到一个刚体节点，并具有不同的函数形式。此外，连接到同一刚体节点的线性化重投影因子组合成一个单一因子，由叠加3个重投影因子表示。如果平面假设被拒绝，则因子图返回到左边的形式。

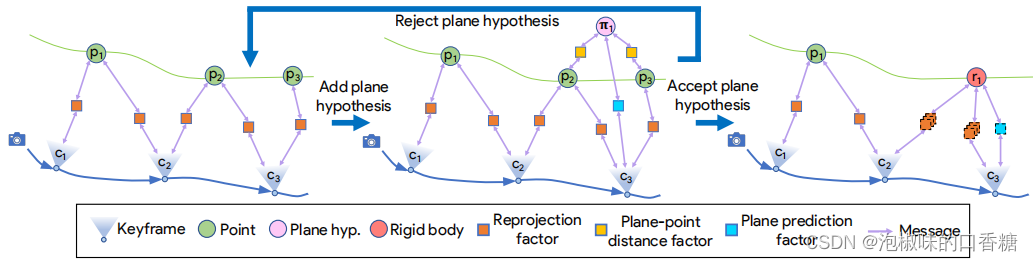
图2 因子图

作者提出了一种基于两个新组件的实时增量构造场景图的通用方法：(1) 增量抽象框架；(2) 通过GBP进行的分布式优化。作者将通过神经网络的摊销推理与通过GBP的分布式概率推理结合到SLAM中的增量抽象因子图中。主场景表示因子图，同时在线操作期间，GBP不断地对该图执行推理。当发生以下情况时，GBP被中断以编辑因子图：(1) 添加一个新的关键帧；(2) 验证平面假设；(3) 合并平面。

综上所述，作者工作的主要贡献如下：

$1$ 使用的增量抽象框架来自现成网络的摊销推理与概率推理相结合，以鲁棒地识别抽象场景元素。此外，在接受场景元素时，作者将连接公共节点的线性化和连接因子，以产生更语义、密集和压缩的表示。

$2$ 通过新的路由过程，作者首次在图处理器上使用GBP来推断动态因子图。GBP每次迭代的时间与图结构无关，作者证明了其结果相比直接法的优势。

$3$ 提出的框架是通用的，可以用于任何抽象的特征检测器。同时添加了平面抽象，它提供了一种紧凑的方式来在许多人造环境中密集地表示几何。

3.1 特征提取和平面预测¶

在关键帧的特征提取方面，作者计划在基于特征点法的单目SLAM系统上构造抽象场景图，即选择一个稀疏SLAM前端，并集中在图形后端。在具体实验环节，作者使用ORB-SLAM2前端来构建由关键帧、点和重投影因子组成的因子图(如图2左所示)。重投影因子惩罚关键帧c中图像坐标z处的匹配特征与图像平面上对应点p的投影之间的距离：

在整合平面预测方面，对于每个关键帧，作者运行一个平面RCNN模型的前向传递来预测一组平面参数和相应的分割掩模。在具体实验中，作者使用的模型是Mask RCNN，并带有一个额外的头部来回归平面法线。具体做法是，对预测进行过滤，以去除具有小的或断开的分割掩模的平面。然后将得到的平面假设作为平面假设节点集成到现有的因子图中(如图2中间所示)。利用每个平面的分割掩模，可以确定预测位于该平面上的映射点，并引入平面-点距离因子，将假设的平面π与每个这些点p连接起来。平面点距离因子影响从一个点到一个平面的垂直距离，其形式为：

每个平面假设π也与关键帧c相连，其中它通过一个平面预测因子进行预测。平面预测因子将平面参数π_z的网络预测作为测量值，其形式为：

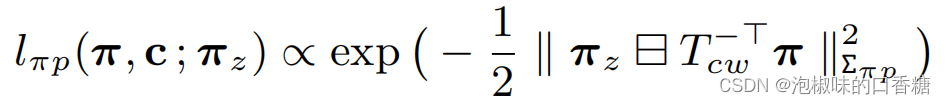
此外，作者也提到，他们的框架不是特定于平面的，任何具有适当兼容性因子和推理模型的抽象场景元素都可以用来生成假设。

3.2 平面假设的确认和拒绝¶

在将平面假设添加到原始因子图后，GBP对混合图(图2中间)进行推断，并收敛到使因子能量最小的构型。为了允许坏平面假设被视为离群测量值，并且只对图结构的能量贡献很小，作者通过协方差调整对所有因素使用鲁棒的Tukey损失函数。收敛后，对于每个平面假设，通过所有的连通点，并从因子图中读取该点位于平面上的可能性，确认和拒绝的标准为：

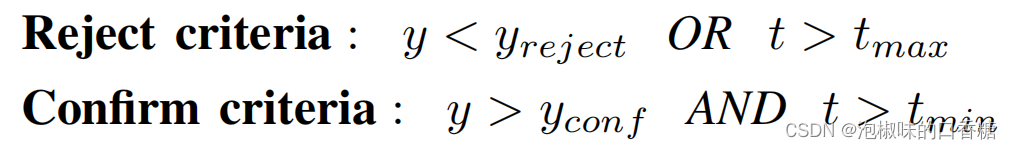
如果被拒绝，则从图中删除平面假设节点和所有相邻的因子。如果得到确认，将似然平面假设节点和点替换为只有6个自由度的刚体可变节点。

3.3 合并平面¶

由于对于同一几何平面可能有多个平面假设，需要合并确认的平面，这些平面具有如下特性：(1) 对齐的法向量；(2) 小的垂直间隔； (3) 大量重叠。其中，后两个标准是通过平面上的采样点来估计的。一旦两个平面被选择合并，就用一个刚体平面替换两个刚体平面。新的平面法线是合并法线的平均值，连接到合并平面的因子被转移到新的平面。

3.4 IPU上的动态路由¶

作者在单个Graphcore MK1 IPU芯片上实现了他们提出的增量抽象方法，IPU是一个由1216个独立的内核组成的大型芯片，这些内核以全连接图形结构排列。类似GPU，IPU是高度并行的，但由于其互连结构和每个内核上的本地内存，它对于具有稀疏消息传递特征的算法具有突破性的性能。

作者的路由解决方案引入了密集连接的路由节点，通过因子图来协调消息的传输。路由节点知道存储在路由矩阵中的因子图的一部分的结构。如图3所示，当编辑因子图时，可以更新路由矩阵，以便能够在新的因子图上进行推断，而不改变编译的通信模式。为了分配路由，作者为每种因子类型创建一个路由节点。

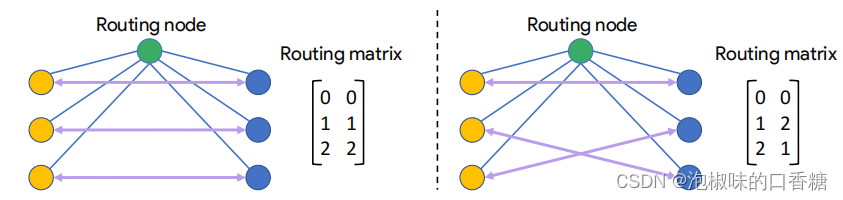
图3 路由过程

黄色和蓝色的节点是不同类型的节点，紫色的线表示因子图中的边，蓝线表示硬件核心之间的通信边

4. 实验¶

在实验阶段，作者使用了利用Kinect相机在不同室内环境中捕获的真实序列和来自TUM数据集的序列，还与使用GBP进行推理但没有平面抽象的GBP-BL方法进行了比较。

4.1 收敛时间评估¶

作者评估了基于不同类型因子图的BA问题的收敛时间。具体方法为，从一个包含35个关键帧、3108个点和10000个重投影因子的因子图开始，并从噪声初始化中测量收敛时间。然后，向图中添加200个新类型的附加因子以及任何新的变量节点，并重复实验。实验设备为18线程 6核i7-8700K CPU，Ceres使用Levenberg-Marquardt (LM)算法，实验结果如图4所示。

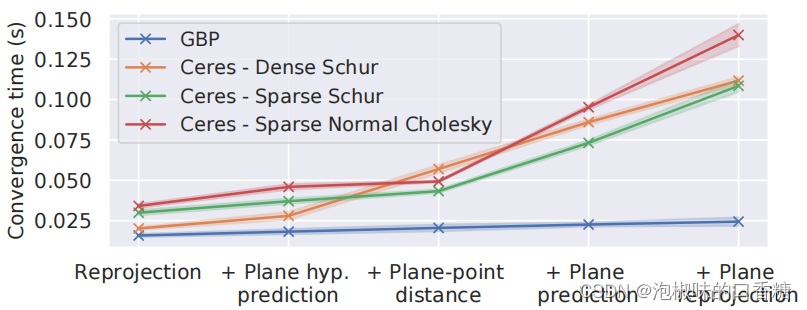
图4 10次运行的平均值和标准偏差误差数据

Ceres通过LM进行最优的全局更新，并且在5-10次迭代中收敛，而GBP需要20-25次迭代，但GBP每次迭代的时间更少。结果显示，随着图结构中加入不同类型的因子，Ceres的收敛时间大大增加，而GBP仅略有增加。同时，作者也提出将收敛时间分解为每次迭代的时间和迭代次数的乘积是很有指导意义的。

4.2 定性重建¶

如图5所示，作者展示了4个序列的平面重建。其中顶部表示由系统恢复的平面重建。底部表示使用深度获得的场景的可视化。重建(a) (b) ©来自于Kinect相机捕获的序列，(d)来自于TUM序列。在(d)中，作者验证了对于一个简单的平面场景，系统可以实现一个完整的重建。图1显示了带有点的相同序列的中间重建过程。

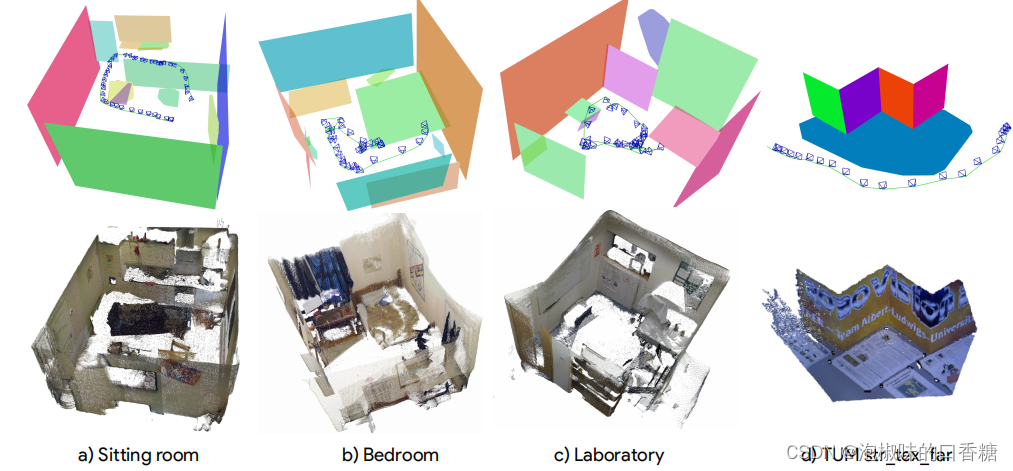
图5 定性重建结果

4.3 压缩评估¶

图形压缩可以产生更密集、语义和参数有效的表示，并减少GBP每次迭代的计算量。当所有因子都是成对的时，计算与边的数量或等价的因子的数量成比例。如图6所示，为了量化系统的压缩能力，作者比较了图结构中的因子节点的数量和GBP-BL。结果显示，对于作者提出的平面系统，随着许多平面假设的加入，最初有很多因子，但是随着平面的确认，图结构被快速压缩。压缩在实验室和TUMstrtex序列中最为重要，因为场景中有大的纹理墙，而在客厅序列中由于大的弯曲物体如沙发的压缩较小。

图6 序列中的因子节点个数

4.4 跟踪评估¶

如表1所示，作者评估了3个TUM序列的绝对轨迹误差(ATE)，作者比较了完整方法和两个消融方法：未压缩平面方案和与Ceres性能类似的GBP-BL系统。

结果显示，作者的未压缩方案(-C)的ATE低于GBP-BL，这表明平面约束有助于跟踪。因为压缩是有损的，所以完整方法的性能比压缩方案略差。但是差异很小，这也表明压缩是准确的。此外，作者的跟踪与ORB-SLAM2性能相当，甚至在一个慢动作序列和多个平面上实现较低的ATE。由于作者提出的方案和GBP-BL都缺乏跟踪系统，因此当添加新帧时，接收到的初始化比ORB-SLAM2更差，这也就是为什么在两个序列上性能较差。因此，作者提出在GBP框架内设计一个分布式跟踪系统是一个重要的研究方向。

表1 ATE对比

5. 结论¶

在2022 CVPR论文"Incremental Abstraction in Distributed Probabilistic SLAM Graphs"中，作者提出了一种基于两个新组件的从单目输入高效增量构建概率场景图的方法。首先，增量式场景抽象框架将摊销推理与概率推理相结合，以识别抽象场景元素并构建语义、密集和紧凑的表示。结果表明，通过平面抽象，系统可以在显著压缩的情况下实现精确的重建。第二，路由过程支持在图形处理器上使用GBP对动态图形进行推理。由于每次迭代的结构不可知时间，作者证明了GBP相对于基于复杂因子图的直接法的优势。