前言¶
这个系列已经更新了20多篇了,感谢一直以来大家的支持和等待。前面已经介绍过MobileNet V1,MobileNet V2,MobileNet V3,ShuffleNet V1这几个针对移动端设计的高效网络,ShuffleNetV2是ShuffleNetV1的升级版,今天就一起来看看这篇论文。论文原文见附录。
介绍¶
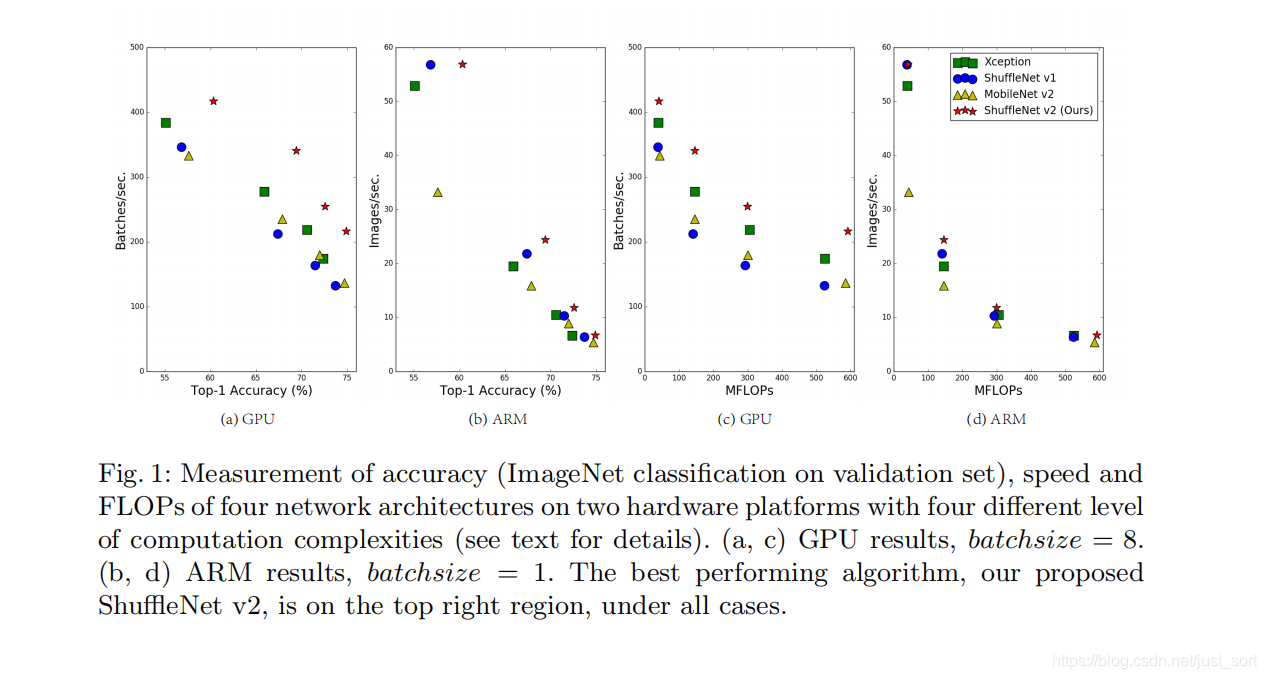
论文首先指出目前大部分的模型加速和压缩的论文在对比加速效果时的指标都是FLOPS,这个指标主要衡量的就是乘法和加法指令的数量。而这篇论文通过一系列实验发现FLOPS并不能完全衡量模型的速度。如Figure1(c)和(d)所示,在FLOPS相同的情况下,速度却有较大的区别。所以接下来就针对相同FLOPS会出现速度差异的这个问题,做了一系列工程实验,并在ShuffleNet V1的基础上提出方法进行改进就得到ShuffleNet V2了。
关键点¶
论文提出除了FLOPS之外,内存访问消耗的时间是需要计算的,这对速度的影响也比较大。这个指标是后续一些实验的优化目标,下面就将每个实验独立出来理解一下。
实验1¶
探索卷积层的输入输出特征通道数对MAC指标的影响。
实验结论是卷积层的输入和输出特征数相等时MAC最小,此时模型的速度最快。
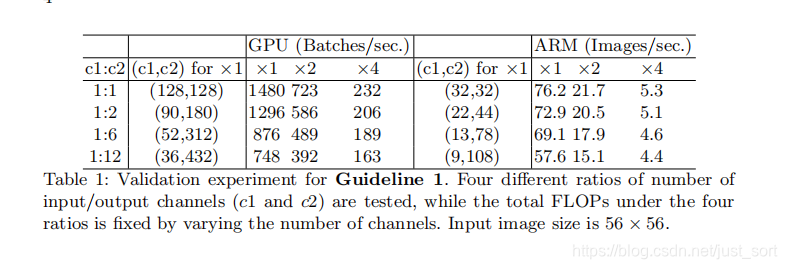
这里的结论也可以由理论推导出来,推导过程如下:
假设一个1\times 1卷积层的输入特征图通道数是c1,输入特征图尺寸是h和w,输出特征通道数是c2,那么这样一个1\times 1卷积层的FLOPS就是:B = c1*c2*h*w*1*1。
接下来看看存储空间,因为是1\times 1卷积,所以输入特征和输出特征的尺寸是相同的,这里用h和w表示,其中h\times w\times c1表示输入特征所需要的存储空间,h\times w\times c2表示输出特征所需空间,c1\times c2表示卷积核所需存储空间。
所以,MAC=h\times w(c1+c2)+c1\times c2。
根据均值不等式推出:
MAC>=2\sqrt{hwB}+\frac{B}{hw}
再把MAC和B带入式子1就得到(c1-c2)^2 >= 0,因此等式成立的条件是c1=c2,也就是输入特征通道数和输出通道特征数相等时,在给定FLOPs前提下,MAC达到取值的下界。
实验2¶
探索卷积的group操作对MAC的影响。
实验结论是过多的group操作会增大MAC,从而使模型变慢。
Mobilenet V1/V2/V3, ShuffleNet V1,Xception都使用了深度可分离卷积,也就是分组卷积来加速模型,这是因为分组卷积可以大大减少FLOPS。
和前面一样,带group操作的1\times 1卷积的FLOPs如下所示:
B = h\times w\times c1\times c2/g
多了一个除数g,g表示group数量。这是因为每个卷积核都只和c1/g个通道的输入特征做卷积,所以多个一个除数g。
同样MAC为:
MAC=h\times w\times (c1+c2)+\frac{c1\times c2}{g}
这样就能得到MAC和B之间的关系了,如下面的公式所示,可以看出在B不变时,g越大,MAC就越大。
MAC=h\times w(c1+c2)+\frac{c1\times c2}{g}= h\times w\times c1+\frac{Bg}{c1}+\frac{B}{h\times w}。
下面Table2是关于卷积的group参数对模型速度的影响,其中c代表c1+c2的和,通过控制这个参数可以使得每个实验的FLOPS相同,可以看出随着g的不断增大,c也不断增大。这和前面说的在基本不影响FLOPS的前提下,引入分组卷积后可以适当增加网络宽度相吻合。
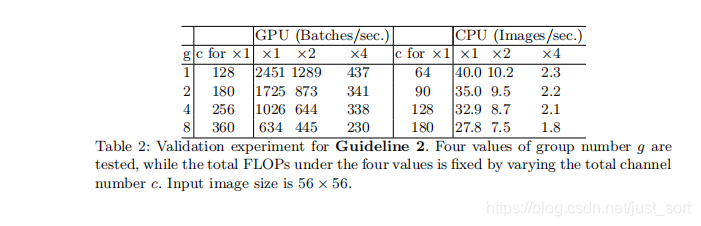
实验3¶
探索模型设计的分支数量对模型速度的影响。
实验结论是模型中的分支数量越少,模型速度越快。
论文用了fragment表示网络的支路数量。这次实验结果如下:
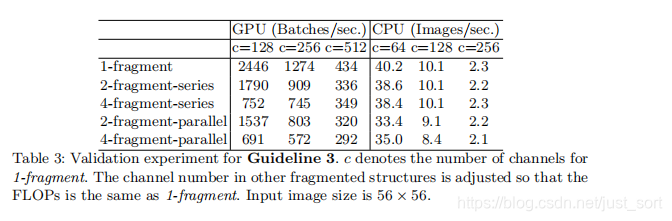
其中2-fragment-series表示一个block中有2个卷积层串行,也就是简单的堆叠。而2-fragment-parallel表示一个block中有2个卷积层并行,类似于Inception的整体设计。可以看出在相同FLOPS的情况下,单卷积层(1-fragment)的速度最快。因此模型支路越多(fragment程度越高)对于并行计算越不利,导致模型变慢,在GPU上这个影响更大,在ARM上影响相对小一点。
实验4¶
探索element-wise操作对模型速度的影响。
实验结论是element-wise操作所带来的时间消耗远比在FLOPS上体现的数值要多,因此要尽可能减少element-wise操作。
在文章开头部分的Figure 2:

可以看到FLOPS主要表示的是卷积层的时间消耗,而ElementWise操作虽然基本不增加FLOPS,但是带来的时间消耗占比却不可忽视。
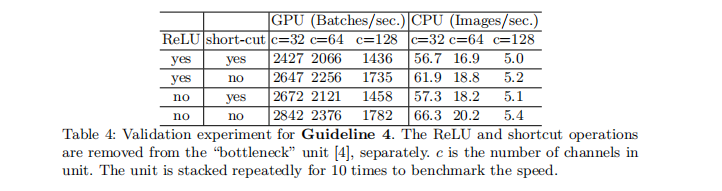
因此论文做了实验4,实验4是运行了10次ResNet的bottleneck来计算的,short-cut表示的就是element-wise操作。同时作者这里也将depthwise convolution归为element-wise操作,因为depthwise-wise convolution也具有低FLOPS,高MAC的特点。实验结果如Table4所示。
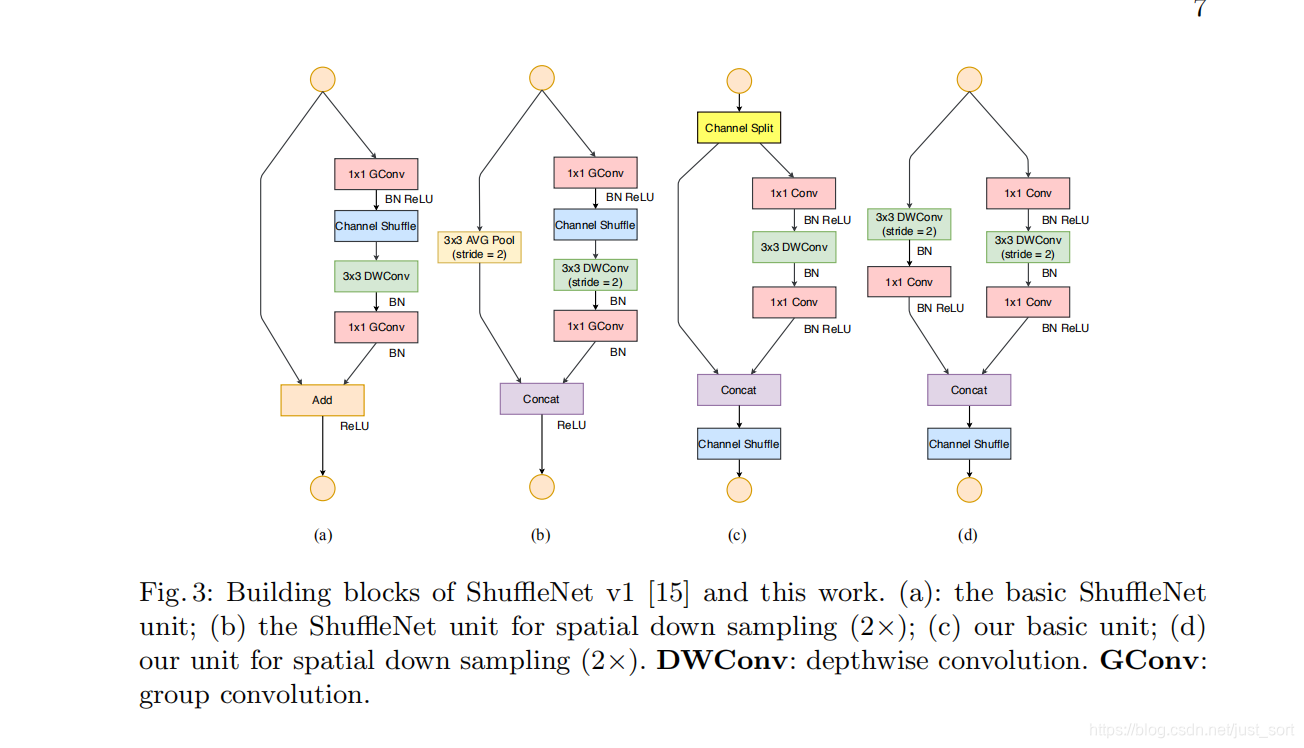
ShuffleNet V2 瓶颈结构设计¶
如Figure3所示。这张图中的(a)和(b)是ShuffleNet V1的两种不同的block结构,两者的差别在于(b)对特征图分辨率做了缩小。(c)和(d)是ShuffleNet V2的两种不同结构。从(a)和(c)对比可知(c)在开头增加了一个通道分离(channel split)操作,这个操作将输入特征通道数c分成了c-c'和c',在论文中c'取c/2,这主要是为了改善实验1。然后(c)取消了1\times 1卷积层中的分组操作,这主要为了改善实验2的结论,同时前面的通道分离其实已经算是变相的分组操作了。其次,channel shuffle操作移动到了concat操作之后,这主要为了改善实验3的结果,同时也是因为第一个1\times 1卷积层没有分组操作,所以在其后面跟channel shuffle也没有太大必要。最后是将element-wise add操作替换成concat,这和前面的实验4的结果对应。(b)和(d)的对比也是同理,只不过因为(d)的开始处没有通道分离操作,所以最后concat后特征图通道数翻倍。
ShuffleNet V2网络结构¶
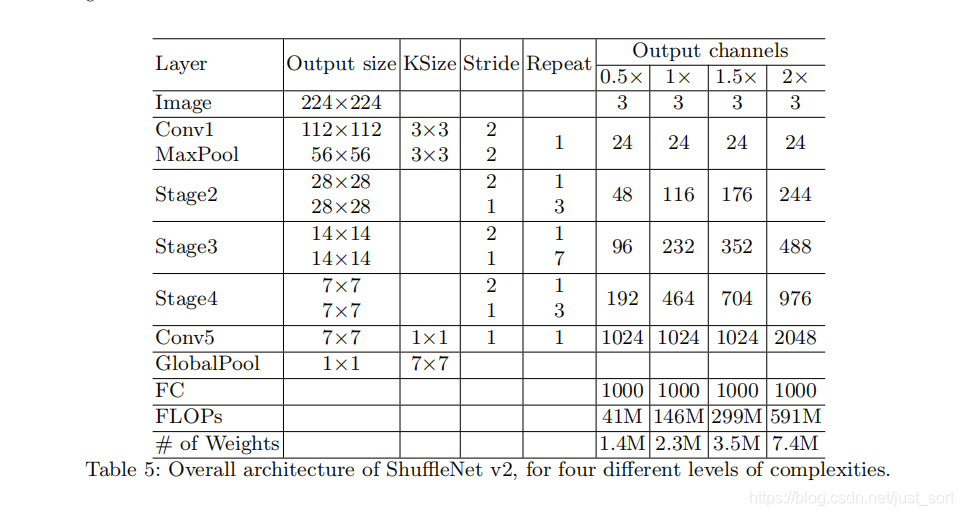
不同stage的输出通道倍数关系和上面介绍bottleneck结构吻合,每个stage都是由Figure3(c)和(d)所示的block组成,block的具体数量对应于Repeat列。
实验结果¶
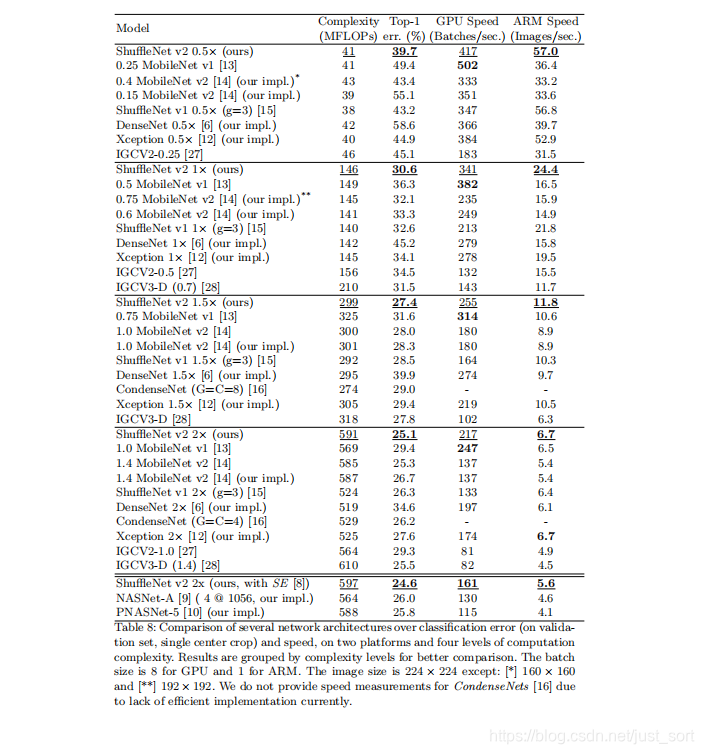
从表中可以看到,ShuffleNet V2在速度和精度上对比众多轻量级网络都是State of Art。
总结¶
论文的构思很像我们在工作时解决问题的方式,先是分析影响模型的速度可能有哪些因素,然后针对这些因素做出一系列实验,最后针对这些实验提出解决方案,最后得出了这个网络。这种思路在整个开发过程中都是通用的。
附录¶
- 论文原文:https://arxiv.org/pdf/1807.11164.pdf
- 代码实现:https://github.com/anlongstory/ShuffleNet_V2-caffe
- 参考1:https://blog.csdn.net/u014380165/article/details/81322175
- 参考2:https://zhuanlan.zhihu.com/p/69286266
推荐阅读¶
- 快2020年了,你还在为深度学习调参而烦恼吗?
- 卷积神经网络学习路线(七)| 经典网络回顾之AlexNet
- 卷积神经网络学习路线(八)| 经典网络回顾之ZFNet和VGGNet
- 卷积神经网络学习路线(九)| 经典网络回顾之GoogLeNet系列
- 卷积神经网络学习路线(十)| 里程碑式创新的ResNet
- 卷积神经网络学习路线(十一)| Stochastic Depth(随机深度网络)
- 卷积神经网络学习路线(十二)| 继往开来的DenseNet
- 卷积神经网络学习路线(十三)| CVPR2017 Deep Pyramidal Residual Networks
- 卷积神经网络学习路线(十四) | CVPR 2017 ResNeXt(ResNet进化版)
- 卷积神经网络学习路线(十五) | NIPS 2017 DPN双路网络
- 卷积神经网络学习路线(十六) | ICLR 2017 SqueezeNet
- 卷积神经网络学习路线(十七) | Google CVPR 2017 MobileNet V1
- 卷积神经网络学习路线(十八) | Google CVPR 2018 MobileNet V2
- 卷积神经网络学习路线(十九) | 旷世科技 2017 ShuffleNetV1
- 卷积神经网络学习路线(二十) | Google ICCV 2019 MobileNet V3
欢迎关注GiantPandaCV, 在这里你将看到独家的深度学习分享,坚持原创,每天分享我们学习到的新鲜知识。( • ̀ω•́ )✧
有对文章相关的问题,或者想要加入交流群,欢迎添加BBuf微信:

本文总阅读量次