跳转至

ResNet的堆叠与数值方法

本文主要从三个方面来讨论DNN堆叠和数值方法之间的联系，以ResNet为例，但不仅仅是ResNet。

  1. 为什么要这么做？数值方法和DNN之间的联系是什么？

  2. 如何去做这件事？实践上的区别和提升是什么？

  3. 实验中观察到了什么，总结出了什么？后续有什么猜测和计划？

ODE和DNN的联系 (为什么要结合数值方法来讨论DNN)

有关这一系列工作的起源详情请看LM-ResNet[1]的作者2prime大佬当时的一个总结介绍：https://zhuanlan.zhihu.com/p/51514687

如果没有兴趣从头了解，直接来看结论也是没有太大影响的。ODE和近几年大热的DNN冥冥之中有着千丝万缕的联系。像ResNet, DenseNet，设计的时候似乎并没有考虑到数值形式，是后来被归纳进去的。

有的则依据ODE的理论进行了设计，比如LM-ResNet，依据的是线性多步。随着越来越多的网络被归纳进来，就不禁让人疑惑，ODE理论是否能够为NN的设计提供宏观上的指导？

神经网络合OED理论之间的联系

一般来说，我们在讨论与对比两个网络的时候，理论依据其实是稍显欠缺。虽然我们通常可以找到一些说法，比如扩大了感受野，融合了多重特征。但这些都更像是一种对结果和现象的解释和补充。

当然了，我不是说DNN完全不具备理论，当然有很多出色的理论解释。不过总体上，DNN在很多时候仍旧比较黑盒。

Dynamical system是几个解释理论之一，如上图所示，许多网络设计都被概括在其中。18年的时候，NODEs更是获得了NIPS18的Best paper。

Neural Ordinary Differential Equations [2] (DNN和ODE之间的联系到底是什么)

它的核心内容是把DNN看做离散化特例，那么如果DNN的层数拓展到无限深，每一层到下一层之间的步长无限小，就自然化为了连续的形式。 NODEs把input到output的mapping过程化为一个在特定点求解ODE的初值问题，引入了ODE求解器来完成，从而实现了O(1)参数量。

Neural Ordinary Differential Equations论文介绍

非常精彩漂亮的一篇文章，并且提供了一个ODESolver library，极大的引发了人们对这个方向的关注。

那么看到这里结论就比较清楚了。Dynamical system的观点是，DNN是在以一种离散化的方式实现常微分方程。许多不同的网络设计则对应或者部分对应了求数值解的数值方法。

NODEs的视角是从离散到连续，而我们所讨论的堆叠方式则是反过来，从连续到离散。

为什么要从连续回到离散？（为什么要这么做）

NODEs已经归纳出了连续的方式，为什么还要重新回到离散呢？ 这是因为目前的情况下，完全连续所需要的计算量确实太大了。如果采用的方法高阶，更是会成倍增长。我们根据高阶办法反过来对现在常用的网络进行调整和修改，是为了实现有理论支持的，离散DNN设计，有依据地对网络进行提升和改进。实验也证明，在不引入额外参数的情况下，很多地方都可以依据数值方法而获益。

在使用NODEs的求解器的时候，我们可以大概观察到一个正比的关系。在求解精度设置一致的情况下，如果求解器所使用的方法是更高阶的数值方法，那么最后NN的性能大多数情况下会有所提升。但是在NODE定参数的情况下，这样做会急剧提升浮点运算次数，从实践上看，似乎不是那么划算。

Block堆叠和数值方法 （如何去做这件事）

长久以来，DNN的设计都以sub-net为主。VGG风格的两层3x3或者是bottleneck。这其实很好理解，ResNet突然把深度从十几层拉到1000层，人为的设计每一层确实显得不那么合理。这种从ResNet开启的2-3层乘以X就形成了XXNet(subnet,[S1,S2,S3,S4])的模型构筑风格。在最新的ResNet-RS中甚至有单个stage可以堆叠84个ResBlock。我们认为，在不考虑sub-net设计的情况下，blocks之间的关联也应该得到重视。

因为前人已经做了很多Sub-net设计的工作，因此这次考虑数值方法的时候，我们的视角更多的放在了block之间的链接上。在layer之间每两层就要加一个shortcut，如果把2-3层的sub-net看作是一层layer，直接前向堆叠几十次的做法感觉上收益会迅速递减。

在这里插入图片描述

有一张数值方法的图可以很好的表达为什么我们可以从高阶的堆叠方式中获取收益。

LR与初始状态 （直接堆叠的缺陷）

以ResNet为例，kaiming大神提出ResNet的时候是为了解决深层不进反退问题。虽然ResNet非常简洁优雅地，极大地缓解了这个现象，并成为DL里程碑式网络，但在他的论文中结果其实也显示，1000层的ResNet还是退了。在我的实验中，不仅1000层的ResNet退了，不到100层的ResNet也出现了退化情况。这并不是说它们不能够取得比浅层更好的结果，而是它们对LR和初始状态这样的超参数非常敏感。

梯度的消失和爆炸都与链式法则密切相关，细微的差别在极深的网络中会被传播放大，而如上图所示，欧拉法对比更高阶的方法更容易有误差。在CIRAR-10上，如果你用0.1LR的SGD训练一个小于40层的网络，效果非常好。但随着深度的持续增加，你就会观察到ResNet的前期收敛明显变得慢了，在极深的情况下仍旧会出现梯度爆炸这个老问题。

这时候如果适当调节学习率，问题就会得到缓解，我相信大家在各种项目中也饱受过学习率之苦，都有过类似的经验。可正因为微调一下学习率就解决了问题，这才让人很容易忽视背后的问题。我们经过试验发现，在大lr导致较深ResNet早期收敛变慢的时候，高阶的ResNet仍旧可以一切如常，快速收敛。其现象与上图所示一致。我们特意寻找到ResNet会梯度爆炸的设置，高阶堆叠的ResNet同样可以正常快速的收敛。

基于这个现象，我们对鲁棒性也进行了进一步的测试。假设一个非常简单的情况，Conv(3,64)，然后堆叠N个(64,64)维度的VGG风格双层3x3的block。整个过程中，仅有一次stride=2的feature下采样。对比两种情况：

1，下采样发生在Conv(3,64)阶段，在升维的过程中，下采样。

2.在第一个Conv(64,64)layer下采样。结果一个简单变化，Baseline ResNet的性能就发生了较大的波动，而高阶堆叠的ResNet则非常稳定。

同参数的堆叠对比 （实质上的提升）

高阶方法之所以繁琐，是因为在同步长情况下进行了更多次运算，计算了更多的中间状态以获得更为精确的数值。这也是为什么前文说到，NODEs中调用求解器，高阶办法需要几倍的浮点运算次数。

而我们设计的对比实验中，在离散的情况下，则是把反复堆叠的低阶办法看作是一种另类的高阶办法。以实际参数量和符点运算次数相等的情况来做公平对比，因此虽然名义上是高阶堆叠的ResNet，但由于Block的数量不同，在对比的过程中是完全同层数，深度，参数量和计算量的。

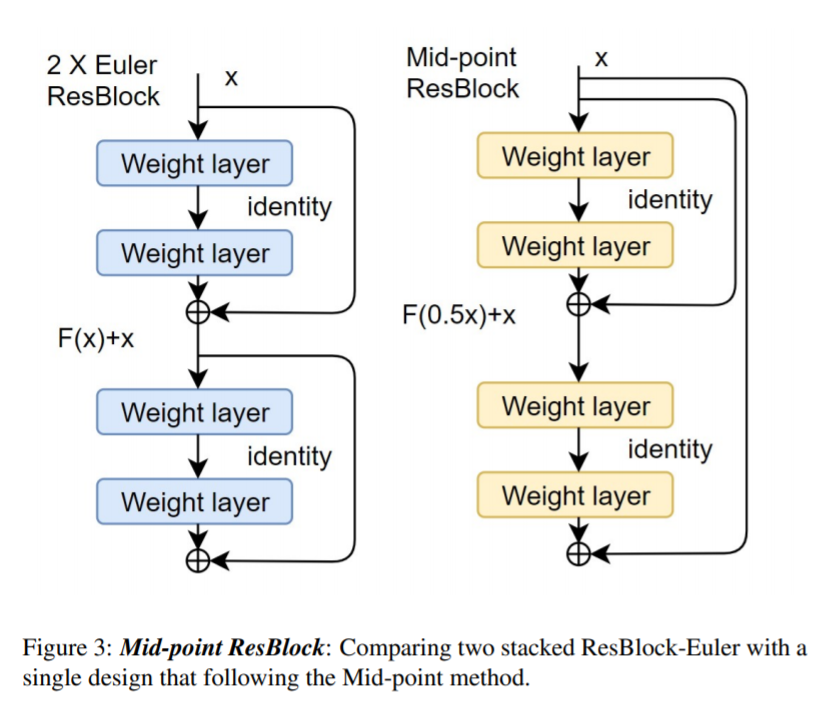
image

以ResNet-50为例，如采用VGG风格的2层3x3设计。标准ResNet也就是欧拉前向法，就应当是堆叠24次。Res-50(2+2x24)。若采用二阶办法，则只堆叠12次来公平对比，为2+4x12。

在这里插入图片描述

若为四阶，则是2+8x6。 如此一来，高阶办法的弊端就得到了极大的缓解。而即便在这种情况下，这种堆叠方式同样可以带来显著的提升。

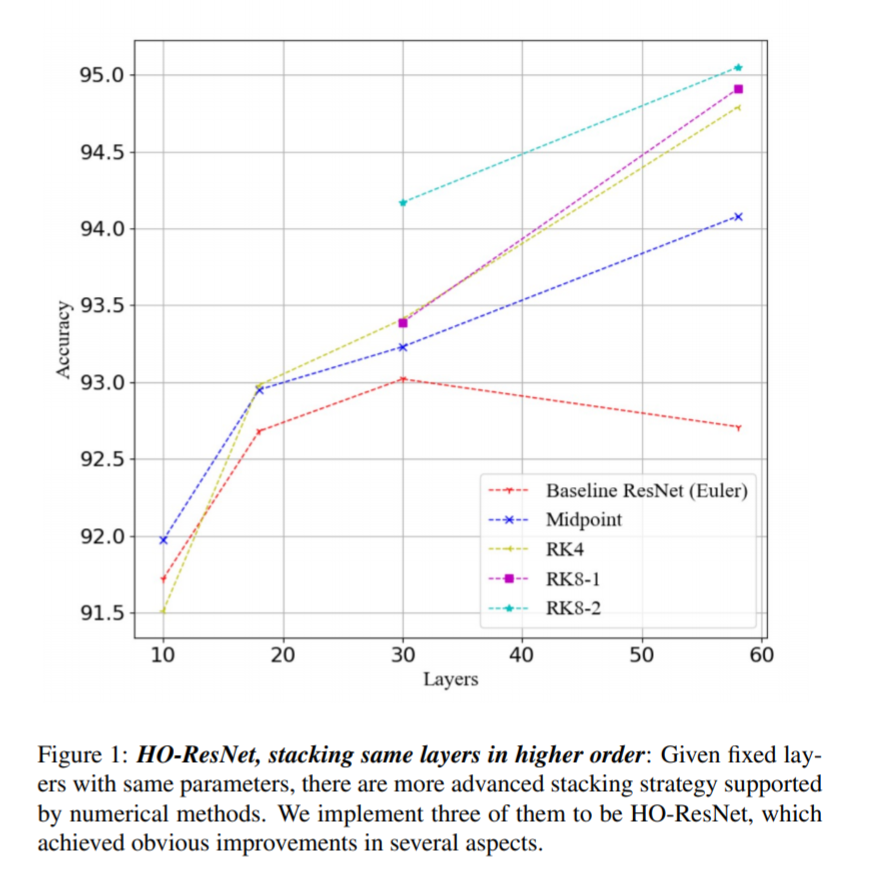
image

这种提升在浅层的时候差距很小，但随着深度的增加逐渐拉大，我们观测到的这个现象，也是符合上面不同阶数值方法的误差情况的。

在具有一定深度的情况下，不论是具体性能还是收敛的情况，都随着方法的阶数上升而获得了相应的提升。大家总说训网络是玄学，炼丹，这次能有这么清晰，性能按阶数逐步增强，差距随深度加深变大，这么符合理论的结果出现，说实话我个人也是吃了一惊。

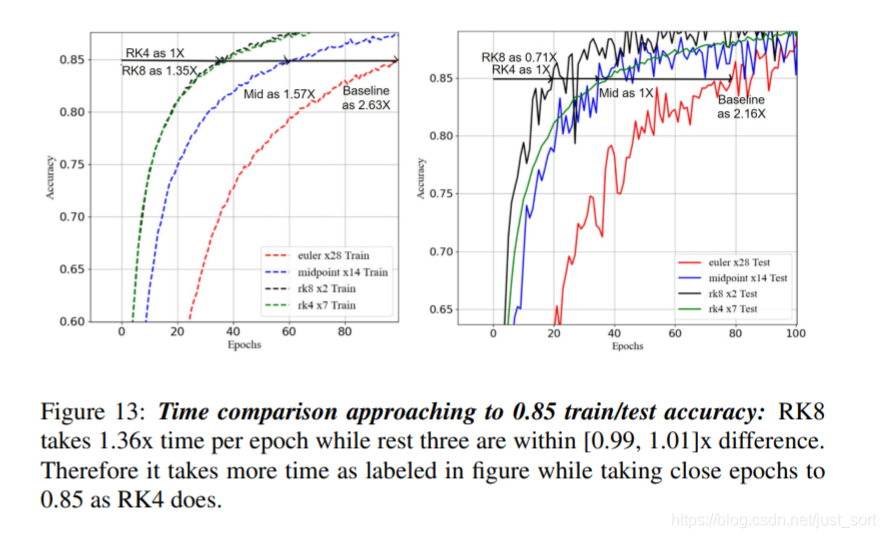
在这里插入图片描述

在CIFAR10上的实验结果

有关实验的一些事情 （观察到了什么）

退化现象

从上面的总结图中，看到ResNet在58层相比30多层退化了，这主要是因为我没有改动任何设置。如果微调学习率，增加训练epoch，还是可以取得更高的结果的。当时写预印本的时候后面100多层的实验也还没做完。实际上如果继续对比100层的情况，二阶和三阶办法也出现了退化或者说无提升的情况。这也是符合误差情况的，在预料之中。四阶办法则能够继续保持提升。不过我估计再加点深度，恐怕也会有退化情况出现。

所以说ResNet并没有彻底解决退化问题，只是缓解。而高阶ResNet同样没有彻底解决退化问题，仍然也只是缓解。这其实可以理解，数值解比起解析解总归有误差的，只要有误差，极深的NN必然会链式放大它。只不过随着阶数的提升，使用高阶堆叠的模型可以对LR等超参数更加鲁棒，因为传播出去的误差被极大的抑制了。

嵌套

堆叠的高阶block可以看做layer继续嵌套建立全局关系，如此一来网络设计就不是sub-net x N的格式，而是整体设计。单纯的堆叠对比，高阶办法的提升很明显，这让我们觉得也许block堆叠越少越好。但直接嵌套的方法并没有取得特别好的效果，早期的收敛加快了，但最后的性能基本上在误差浮动范围之内，没有观察到区别。

自适应系数

二阶，三阶和四阶方法是固定系数的，二分之一，三分之二，二加减根号二之类的。在更高阶方法中，block内的中间状态在shortcut出去的时候会有抑制系数。这个系数会根据每次迭代返回的误差值动态调整。我们目前的实验中暂时还没有找到一个特别好用的变化方法。个人感觉这种形式和SEblock以及多头注意力都有点联系。

数据集

数据集确实太小了，我太穷了嗷。因为要对比不同深度的几个不同阶方法，cifar-10基本上是极限了。常见的数值方法还有好几种，现在还在跑着呢。ImageNet只能指望别人去验证了。目前在Cifar-10上确实非常理想。

下游任务

下游任务其实也试过好几个，但由于负担不起所以没能写进文章里。对U-Net是有提升的，对transformer基本上没有。我个人觉得一可能是因为多头注意力和输入抑制非常类似，再加上我跑的transformer堆叠block也不多，所以没有观察到明显提升。

有关后续工作 （我们的猜测和计划）

堆叠设计的应用范围

因为我们的视角并不在意sub-net的设计，也不被各种trick影响。所以可以应用的范围很广，如果拆去各个任务水一下，应该还是挺好水的。

我们对比的时候基本上把trick去了个精光，因为确实看了很多文章觉得work，后面发现不知道是什么trick在work。

到底是什么在work

主要区别大概是这些：

  1. 高阶办法中的shortcut总是从初始点介入。

  2. 高阶办法中，一个block内的各层状态经常被小于1的系数抑制。

  3. 在非常高阶的办法中，中间hidden state的状态会依赖更多的中间层。

我自己控制变量测了一下，如果直接在ResNet上修改，2的提升是最方便也最明显的。

从block堆叠引申出去

我们后续对常见的10种数值办法进行了测试，发现如果把相同的层数以不同阶数的方式链接起来，在同设置下收敛和性能的提升基本上是随阶数提升而增长的。

虽然对同一设计进行反复堆叠是比较常见的情况，但是如果没有像Backbone里那样堆叠太多次，使用高阶办法的效果就不会特别明显。

不过数值方法也只是很小的一部分内容，对于比较浅层的设计，我们相信还有很多其他数值方法或者其他领域的理论值得探索。

可视化权重surface或者loss surface [3]

根据[3]在17年对常见的DNN进行的可视化，ResNet和DenseNet引入的诸多链接极大地平滑了 loss surface。我们后续计划对不同深度，不同阶数的链接方式做Loss surface的对比和可视化。

虽然暂时还没有结果，但我们猜测高阶的loss surface会更加光滑和平缓。

重参数化

二阶方法对RepVGG是有提升的，但更高阶就没有了。说明NN中的高阶堆叠还是依赖非线性的。这和一个block含有几层layer比较好的结果类似，2-3层比较理想，多了少了都会降。

我们的预印本： https://arxiv.org/pdf/2103.15244.pdf

[1] https://arxiv.org/pdf/1710.10121.pdf LM-ResNet链接

[2] https://arxiv.org/pdf/1806.07366.pdf NODEs链接

[3] https://arxiv.org/pdf/1712.09913.pdf Landscape可视化链接

欢迎关注GiantPandaCV, 在这里你将看到独家的深度学习分享，坚持原创，每天分享我们学习到的新鲜知识。( • ̀ω•́ )✧

有对文章相关的问题，或者想要加入交流群，欢迎添加BBuf微信：

二维码

本文总阅读量次