前言¶

之前做的一些滤波，例如高斯，双边，均值，导向滤波均是在时域下做的滤波。而同态滤波是在频域下来做滤波，用于改善动态范围很大但是暗区细节又不清楚的图像。

原理¶

对于一般的图像，有这样一个模型 $f(x,y)=i(x,y)r(x,y)$ 。其中f(x, y)代表原图像，i(x,y)代表照射强度，r(x,y)代表反射强度。一般的图像光照是均匀变化的，所以i应该是低频分量，而不同的物体对光的反射是具有突变型的，所以r(x,y)是高频分量。现在同时对上式两边同时取对数，在做Fourier变化，得到线性组合的频率域：

$ln f(x,y)=ln i(x,y)+lnr(x,y)$

$FFT(lnf(x,y))=FFT(lni(x,y))+FFT(lnr(x,y))$

我们希望对低频能量进行压制，这样就降低了动态范围，而要对高频分量进行提高，这样会增强图像的对比度。因此，同态滤波器的传递函数一般在低频部分小于1，高频部分大于1。

算法过程¶

对原图像f(x,y)取对数，目的是使得图像模型中的乘法运算转化为简单的加法运算： $z(x,y)=lnf(x,y)=lni(x,y)+lnr(x,y)$
再对对数函数做傅里叶变换，将图像转换到频域
$F(z(x,y))=F[lni(x,y)]+F[lnr(x,y)]$ 即 $Z=I+R$
选择适当的传递函数，压缩照射分量 $i(x,y)$ 的变化范围，削弱 $I(u,v)$ ，增强反射分量 $r(x,y)$ 的对比度，所以总结起来就是这个滤波器需要对低频能量进行压制，以降低动态范围，同时要对高频进行提高，以增强图像对比度。所以同态滤波器的传递函数如下：

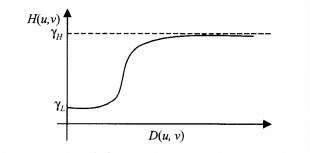
在这里插入图片描述

假设用一个同态滤波器函数 $H(u,v)$ 来处理原图像f(x,y)的对数的傅里叶变换 $Z(u,v)$ 得到： $S(u,v)=H(u,v)Z(u,v)=H(u,v)I(u,v)+H(u,v)R(u,v)$ ，逆变换到时域得： $s(x,y)=F^{-1}(S(u,v))$ ，所以 $f'(x,y)=exp(s(x,y))$ ， $f'(x,y)$ 代表滤波后的图像。整个算法的过程可以用下面的流程图来表示：

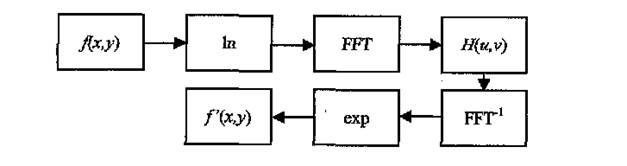
在这里插入图片描述

C++ opencv实现¶

传统的同态滤波器有高斯同态滤波 $H(u,v)_1=(Rh-Rl)[1-exp(-c(D(u,v)/D_0)^{2n})]+Rl$ ，巴特沃斯同态滤波器 $H(u,v)_2=(Rh-Rl)[1/(1+[D_0/cD(u,v)]^{2n})]+RI$ ,指数型同态滤波器： $H(u,v)_3=(Rh-Rl)exp(-c[D_0/D(u,v)])^n+RI$ 。其中 $D(u,v)=[(u-u_0)^2+(v-v_0)^2]^{\frac{1}{2}}$ ,Rh,RI分别为高频和低频增益，D0为截止频率，c是控制斜面锐化的常数。这里实现了第一种滤波器，也就是高斯滤波。

Mat HomoFilter(cv::Mat src){
    src.convertTo(src, CV_64FC1);
    int rows = src.rows;
    int cols = src.cols;
    int m = rows % 2 == 1 ? rows + 1 : rows;
    int n = cols % 2 == 1 ? cols + 1 : cols;
    copyMakeBorder(src, src, 0, m - rows, 0, n - cols, BORDER_CONSTANT, Scalar::all(0));
    rows = src.rows;
    cols = src.cols;
    Mat dst(rows, cols, CV_64FC1);
    //1. ln
    for(int i = 0; i < rows; i++){
        double *srcdata = src.ptr<double>(i);
        double *logdata = src.ptr<double>(i);
        for(int j = 0; j < cols; j++){
            logdata[j] = log(srcdata[j] + 0.0001);
        }
    }
    //2. dct
    Mat mat_dct = Mat::zeros(rows, cols, CV_64FC1);
    dct(src, mat_dct);
    //3. 高斯同态滤波器
    Mat H_u_v;
    double gammaH = 1.5;
    double gammaL = 0.5;
    double C = 1;
    double  d0 = (src.rows / 2) * (src.rows / 2) + (src.cols / 2) * (src.cols / 2);
    double  d2 = 0;
    H_u_v = Mat::zeros(rows, cols, CV_64FC1);
    for(int i = 0; i < rows; i++){
        double * dataH_u_v = H_u_v.ptr<double>(i);
        for(int j = 0; j < cols; j++){
            d2 = pow(i, 2.0) + pow(j, 2.0);
            dataH_u_v[j] = (gammaH - gammaL) * (1 - exp(-C * d2 / d0)) + gammaL;
        }
    }
    H_u_v.ptr<double>(0)[0] = 1.1;
    mat_dct = mat_dct.mul(H_u_v);
    //4. idct
    idct(mat_dct, dst);
    //exp
    for(int i = 0; i < rows; i++){
        double  *srcdata = dst.ptr<double>(i);
        double *dstdata = dst.ptr<double>(i);
        for(int j = 0; j < cols; j++){
            dstdata[j] = exp(srcdata[j]);
        }
    }
    dst.convertTo(dst, CV_8UC1);
    return dst;
}

主函数：

int main(){
    //
    Mat src = cv::imread("./1.png");
   imshow("origin", src);
    int originrows = src.rows;
    int origincols = src.cols;
    Mat dst(src.rows, src.cols, CV_8UC3);
    cvtColor(src, src, COLOR_BGR2YUV);
    vector <Mat> yuv;
    split(src, yuv);
    Mat nowY = yuv[0];
    Mat newY = HomoFilter(nowY);
    Mat tempY(originrows, origincols, CV_8UC1);
    for(int i = 0; i < originrows; i++){
        for(int j = 0; j < origincols; j++){
            tempY.at<uchar>(i, j) = newY.at<uchar>(i, j);
        }
    }
    yuv[0] = tempY;
    merge(yuv, dst);
    cvtColor(dst, dst, COLOR_YUV2BGR);
    imshow("result", dst);
    waitKey(0);
}

效果：

在这里插入图片描述

可以看到图片的整体亮度被拉到人眼可以接受的范围里面了，但是缺点是有些地方出现了白点。再看一组效果：

在这里插入图片描述

我的这个代码效果很不好，如果真的要使用同态滤波需要认真取做研究，可以参考https://github.com/lilingyu/homofilter

本文总阅读量次