Piecewise Linear Unit:分段线性激活函数
前言¶
激活函数在神经网络里是一个重要的组件,大家最常用的是ReLU,其变种在各种任务/模型中都有较好的效果。Swish这种搜索得到的激活函数,在部分数据集上也能超越ReLU,但是搜索效率不够高。
为此我们提出了Piecewise Linear Unit,分段线性激活函数,通过公式设计+可学习参数,能够达到SOTA的结果。

介绍¶
早期的激活函数都是由手工设计的,ReLU凭借其简单,不存在饱和梯度的特性,能够让神经网络快速地收敛。
随后有更多的激活函数被设计出来,他们大部分是形状固定(fixed shape)或带有一部分可学习参数,如 Leaky ReLU, PReLU, ELU, SELU。但是它们在不同任务上效果不同,因此限制了他们的应用范围。
谷歌提出的Swish激活函数是通过搜索得到的,在跨任务场景下展现了更好的性能。然而这种搜索方式过于昂贵,很少人会专门针对自己的数据集重新搜索,所以大多数情况下用的是谷歌搜索得到的Swish版本。
近期也有基于上下文的激活函数提出,说人话就是一种动态的激活函数。
微软于ECCV 2020提出Dynamic ReLU,根据全局信息对ReLU进行参数化,动态调整斜率。
同样是在ECCV 2020,旷视研究院的马宁宁博士提出Funnel ReLU,给ReLU加入了depthwise卷积,捕捉了一个window内的信息。
方法¶
Piecewise Linear Unit的定义¶

上图是一个pwlu的示意图,具体有以下参数:
- 分段数 N
- 左边界B_L,右边界B_R
- 每一段对应的Y轴值,Y_P
- 最左边界的斜率K_L,最右边界的斜率K_R
我们从[B_L, B_R]均匀划分出N段,每一段都有其自己的斜率
往复杂点考虑,我们可以用公式说明上述的关系:

其中

在这个定义下,PWLU有以下特性:
- PWLU可以表示任意连续,有边界的scalar function
- PWLU变换连续,利于求导
- 可以最大限度利用可学习参数
- 由于我们划分段是N等分的,所以在计算,推理中是efficient的
梯度定义¶
这里就不用论文复杂的公式了,很明显梯度就是各个段的斜率。
Learning the Piecewise Linear Unit¶
在PWLU训练之前,我们需要保证其正确地初始化。
一个很直接地方法是将PWLU初始设置为ReLU,即
- B_R = -B_L
- K_R = 1, K_L = 0
这种初始化方法可能会带来以下问题:
输入边界不对齐¶
PWLU中 B_R 和 B_L 是两个很重要的参数,他们限制了可学习的区域。显然,这个区域需要和输入的分布对齐。
举个例子:
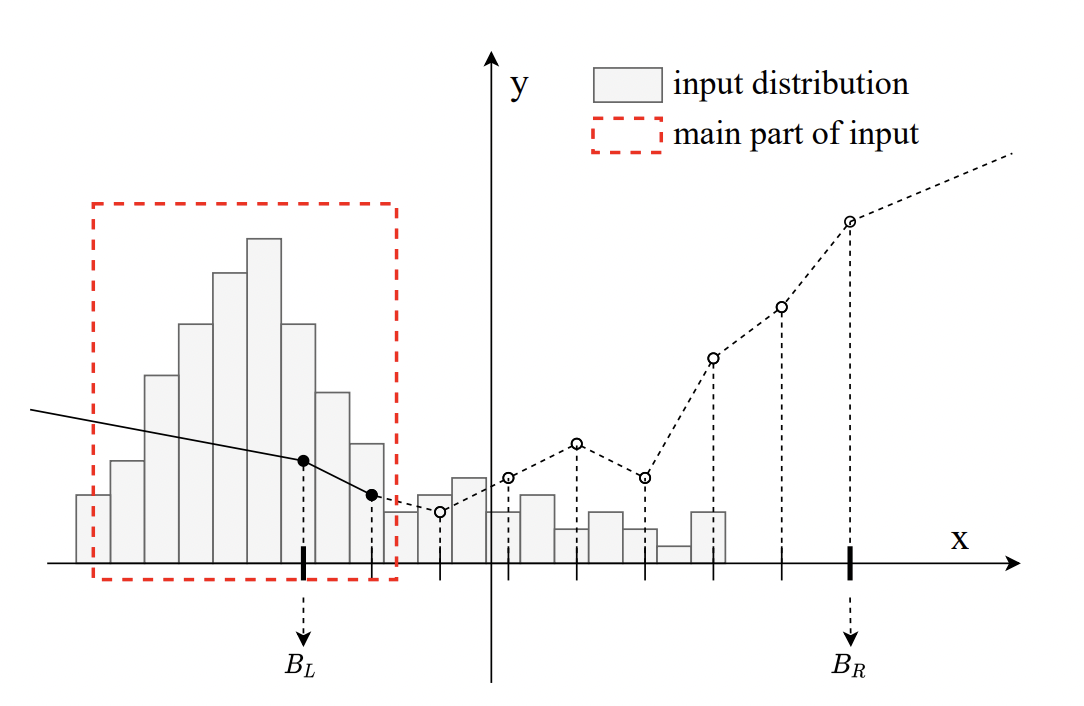
图中输入分布靠左边,那么显然PWLU的右半边就没有起作用,造成参数浪费,影响性能。
解决方法就是通过数学统计重新对齐
具体分为两个阶段:
- 阶段1: 在前面几轮,首先将PWLU设置为ReLU形式,并停止参数更新。计算移动平均得到的均值和方差
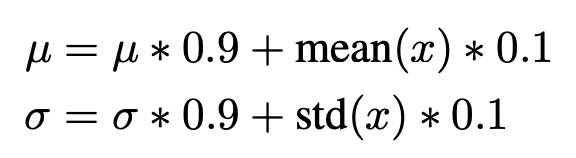
- 阶段2: 开始PWLU的训练,应用3-sigma原则,设置
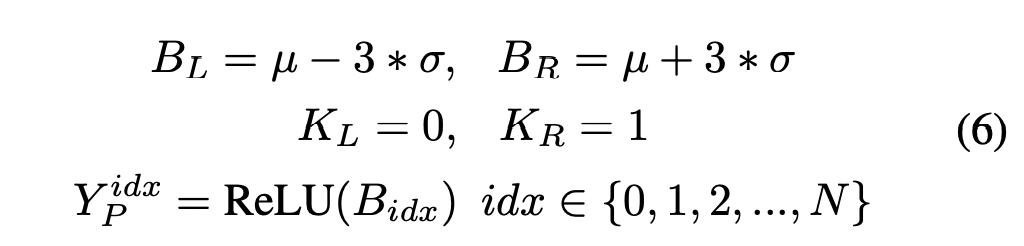
经过前面几轮统计得到的均值和方差,能得到输入的分布,进而应用到PWLU上,对输入边界进行对齐
实验结果¶
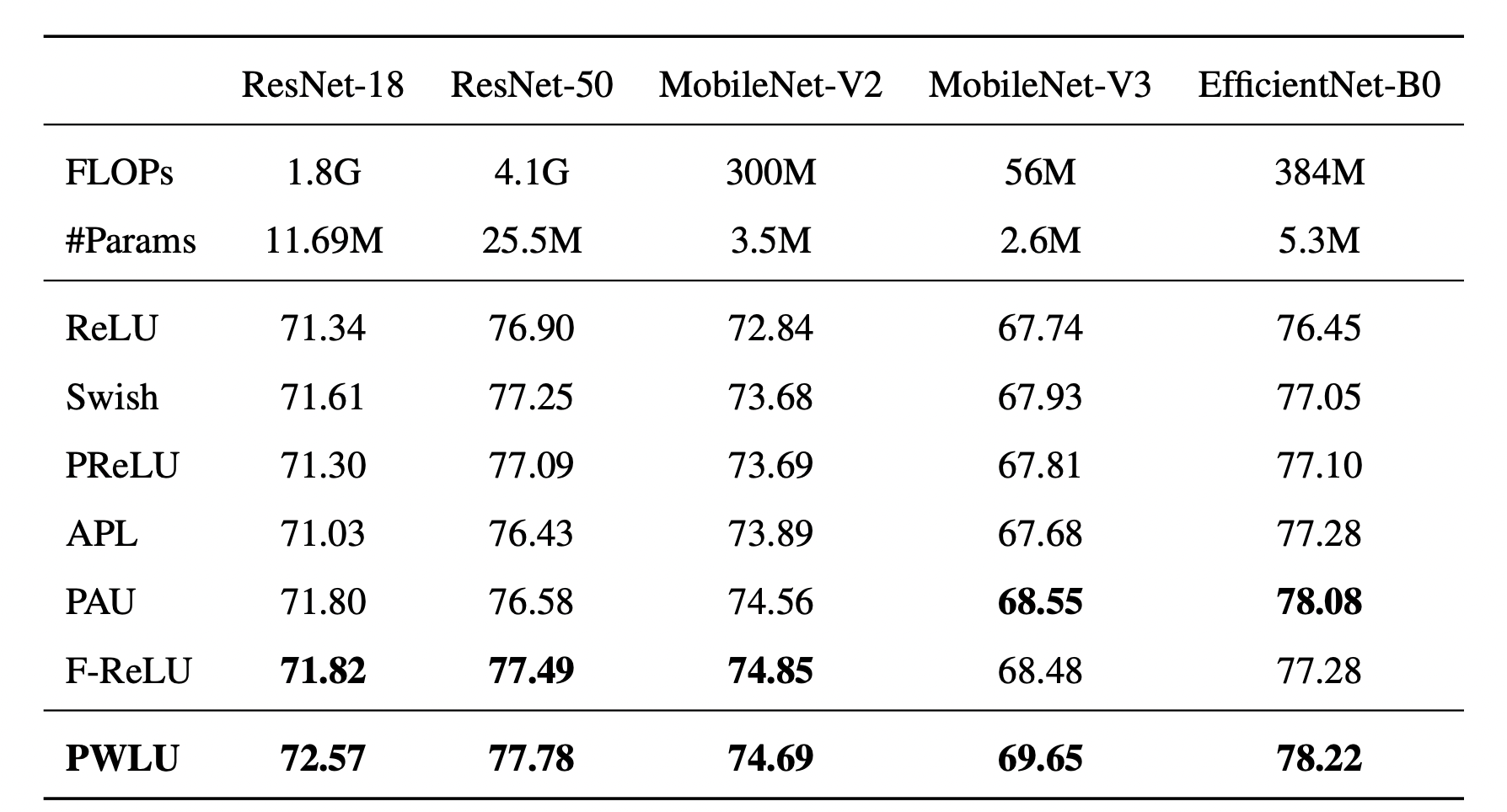
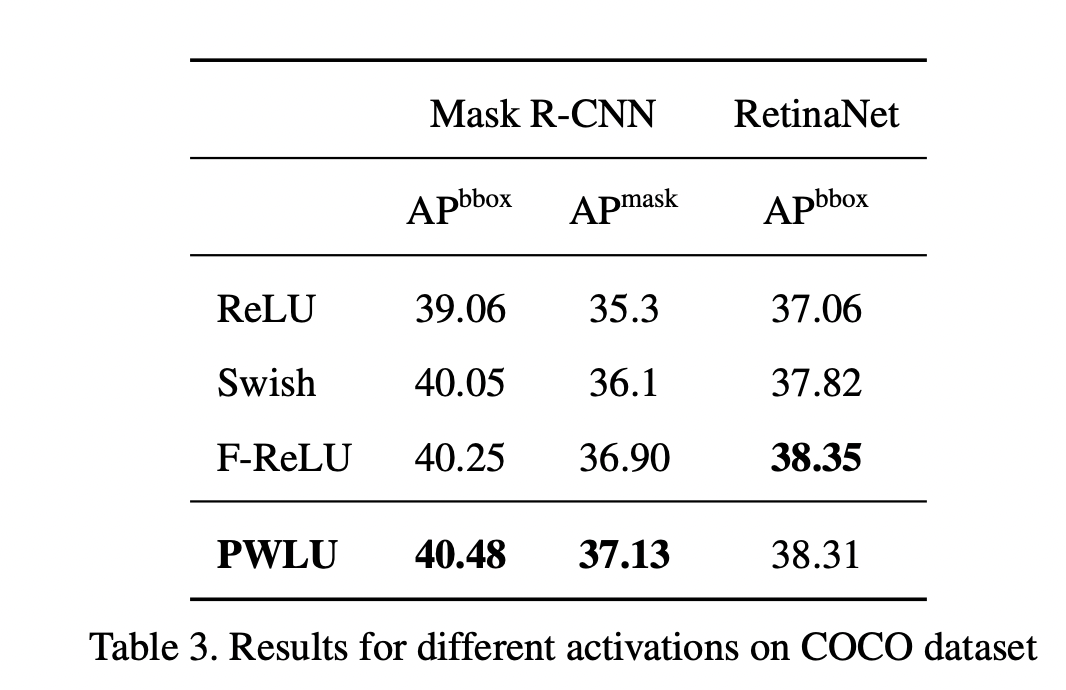
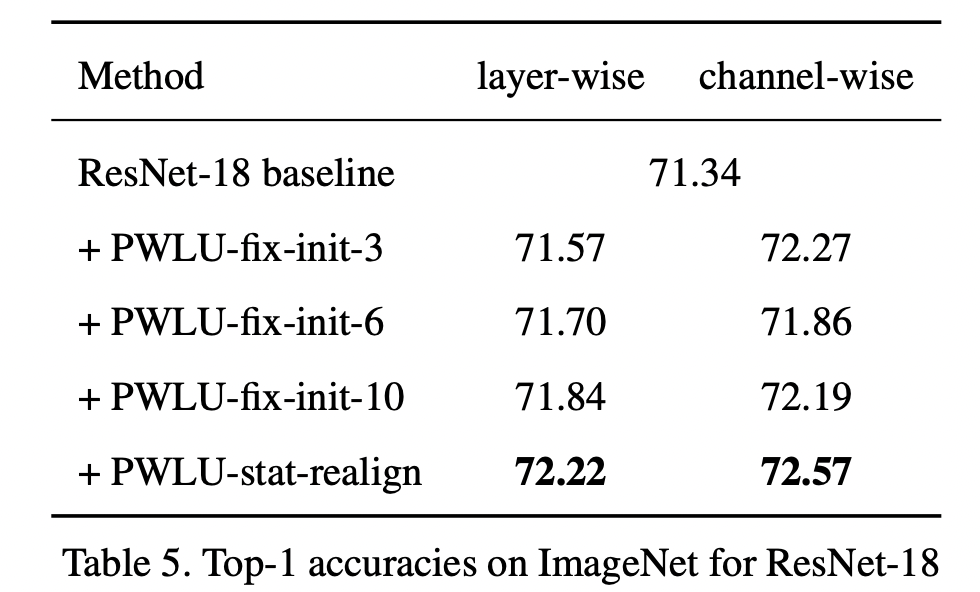
可以看到效果还是不错的,另外作者还做了消融实验,来表明边界对齐的有效性(其中fix-init-X,表示将输入边界固定为[-X, X])
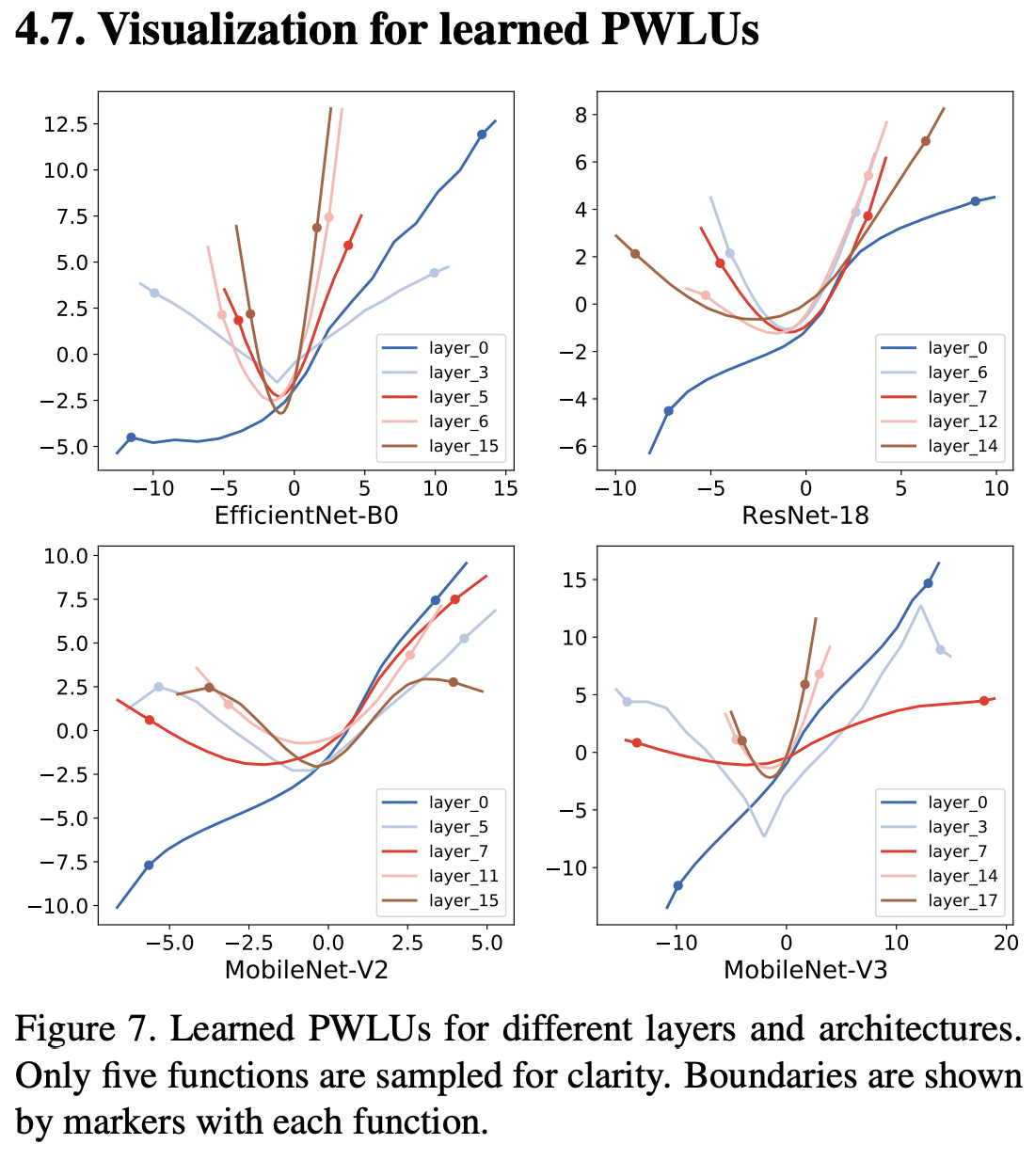
可视化结果¶
我觉得本文的可视化结果是最有趣的一点,通过可视化可以发现较浅的网络层,PWLU表现的更像是一个线性函数,而在较深的网络层,PWLU表现的很抽象,是一个U形函数
非官方代码实现¶
github上有一个非官方代码实现,目前看来实现的有些错误,还不是很完善,仅供参考:
https://github.com/MrGoriay/pwlu-pytorch/blob/main/PWLA.py
总结¶
个人感觉这篇文章还是有点意思的,想法并不复杂,实验也做的很充分。最后一张可视化图更是很有趣
期待作者开源相关代码,也能够方便比较和其他几个激活函数,比较下性能和推理速度。
本文总阅读量次