前言¶
昨天在介绍Center Loss的时候提到了这两个损失函数,今天就来介绍一下。Contrastive Loss是来自Yann LeCun的论文Dimensionality Reduction by Learning an Invariant Mapping,目的是增大分类器的类间差异。而Triplet Loss是在FaceNet论文中的提出来的,原文名字为:FaceNet: A Unified Embedding for Face Recognition and Clustering,是对Contrastive Loss的改进。接下来就一起来看看这两个损失函数。论文原文均见附录。
问题引入¶
假设我们现在有2张人脸图片,我们要进行一个简单的对比任务,就是判断这两张人脸图片是不是对应同一个人,那么我们一般会如何解决?一种简单直接的思路就是提取图片的特征向量,然后去对比两个向量的相似度。但这种简单的做法存在一个明显的问题,那就是CNN提取的特征“类间”区分性真的有那么好吗?昨天我们了解到用SoftMax损失函数训练出的分类模型在Mnist测试集上就表现出“类间”区分边界不大的问题了,使得遭受对抗样本攻击的时候很容易就分类失败。况且人脸识别需要考虑到样本的类别以及数量都是非常多的,这无疑使得直接用特征向量来对比更加困难。
Contrastive Loss¶
针对上面这个问题,孪生网络被提出,大致结构如下所示:
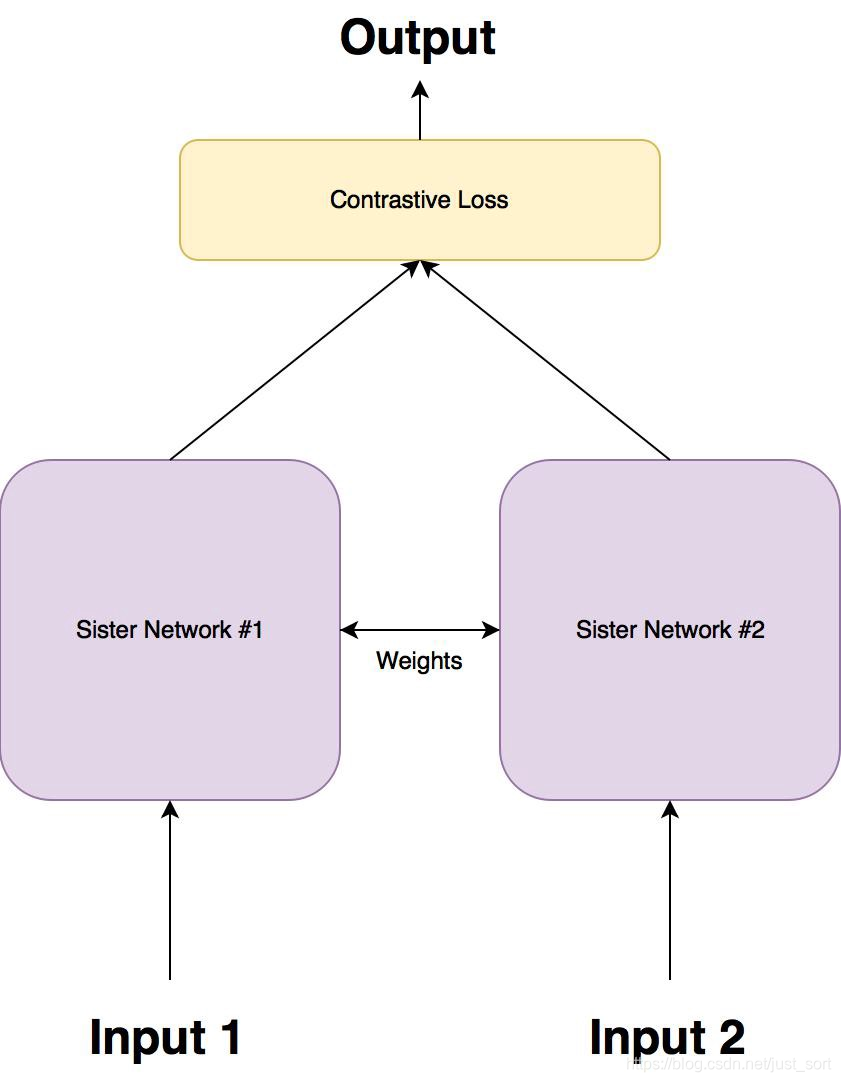
然后孪生网络一般就使用这里要介绍的Contrastive Loss作为损失函数,这种损失函数可以有效的处理这种网络中的成对数据的关系。
Contrastive Loss的公式如下:

其中W是网络权重,Y是成对标签,如果X_1,X_2这对样本属于同一个类,则Y=0,属于不同类则Y=1。D_W是X_1与X_2在潜变量空间的欧几里德距离。当Y=0,调整参数最小化X_1与X_2之间的距离。当Y=1,当X_1与X_2之间距离大于m,则不做优化(省时省力)当X1与 X2 之间的距离小于m, 则增大两者距离到m。下面的公式(4)是将上面的L展开写了一下,如下所示:
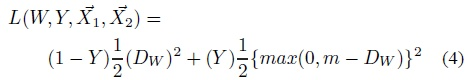
而下面的Figure1展示的就是损失函数L和样本特征的欧氏距离之间的关系,其中红色虚线表示相似样本的损失值,而蓝色实线表示的是不相似样本的损失值。
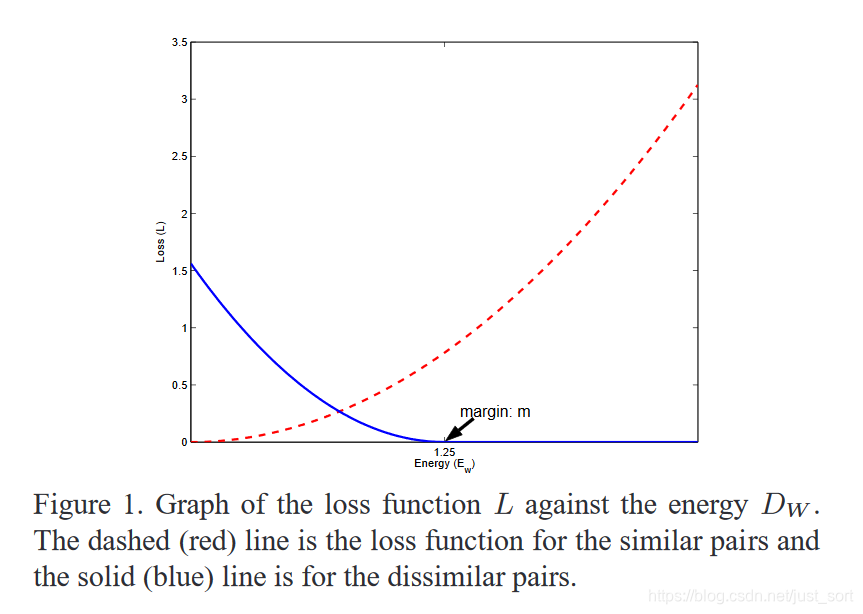
在LeCun的论文中他用弹簧在收缩到一定程度的时候因为受到斥力的原因会恢复到原始长度来形象解释了这个损失函数,如下图:
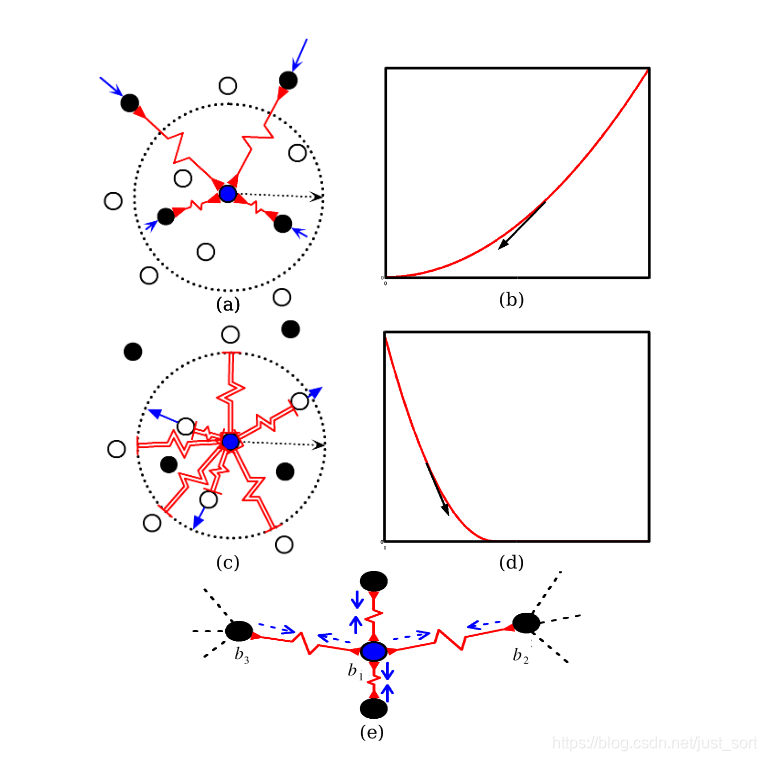
代码实现:
# Custom Contrastive Loss
class ContrastiveLoss(torch.nn.Module):
"""
Contrastive loss function.
Based on: http://yann.lecun.com/exdb/publis/pdf/hadsell-chopra-lecun-06.pdf
"""
def __init__(self, margin=2.0):
super(ContrastiveLoss, self).__init__()
self.margin = margin
def forward(self, output1, output2, label):
euclidean_distance = F.pairwise_distance(output1, output2)
loss_contrastive = torch.mean((1-label) * torch.pow(euclidean_distance, 2) + # calmp夹断用法
(label) * torch.pow(torch.clamp(self.margin - euclidean_distance, min=0.0), 2))
return loss_contrastive
Triplet Loss¶
原理¶
Triplet Loss是Google在2015年发表的FaceNet论文中提出的,论文原文见附录。Triplet Loss即三元组损失,我们详细来介绍一下。
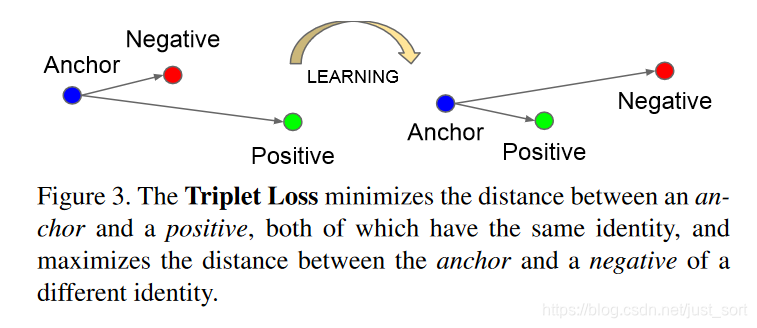
- Triplet Loss定义:最小化锚点和具有相同身份的正样本之间的距离,最小化锚点和具有不同身份的负样本之间的距离。
- Triplet Loss的目标:Triplet Loss的目标是使得相同标签的特征在空间位置上尽量靠近,同时不同标签的特征在空间位置上尽量远离,同时为了不让样本的特征聚合到一个非常小的空间中要求对于同一类的两个正例和一个负例,负例应该比正例的距离至少远
margin。如下图所示:
因为我们期望的是下式成立,即:
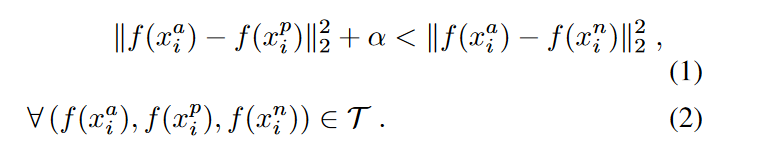
其中\alpha就是上面提到的margin,T就是样本容量为N的数据集的各种三元组。然后根据上式,Triplet Loss可以写成:
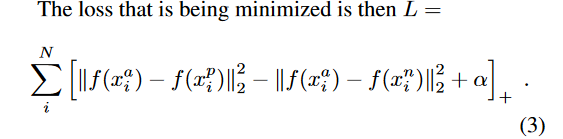
对应的针对三个样本的梯度计算公式为:
\frac{\partial L}{\partial f(x_i^a)}=2*(f(x_i^a)-f(x_i^p))-2*(f(x_i^a)-f(x_i^n))=2*(f(x_i^n)-f(x_i^p)) \frac{\partial L}{\partial f(x_i^p)}=2*(f(x_i^a)-f(x_i^p))*(-1)=2*(f(x_i^p)-f(x_i^a)) \frac{\partial L}{\partial f(x_i^n)}=2*(f(x_i^a)-f(x_i^n))*(-1)=2*(f(x_i^a)-f(x_i^p))
FaceNet¶
我们将三元组重新描述为(a,p,n),那么最小化上面的损失就是就是让锚点a和正样本的距离d(a,p)->0,并使得锚点a和负样本的距离大于d(a,p)+margin,即d(a,n)>d(a,p)+margin。那么三元组的总体距离可以表示为: L=max(d(a,p)-d(a,n)+margin,0)。
FaceNet网络可以更加形象的表示为下图:

所以网络的最终的优化目标是要让a,p的距离近,而a,n的距离远。下面定义一下三种不同优化难度的三元组样本。
easy triplets:代表L=0,即d(a,p)+margin<d(a,n),无需优化,a,p初始距离就很近,a,n初始的距离很远。hard triplets:代表d(a,n)<d(a,p),即a,p的初始距离很远。semi-hard triplets:代表d(a,p)<d(a,n)<d(a,p)+margin,即a,n的距离靠得比较近,但是有一个mergin。 这三种不同的triplets可以用下图来表示:
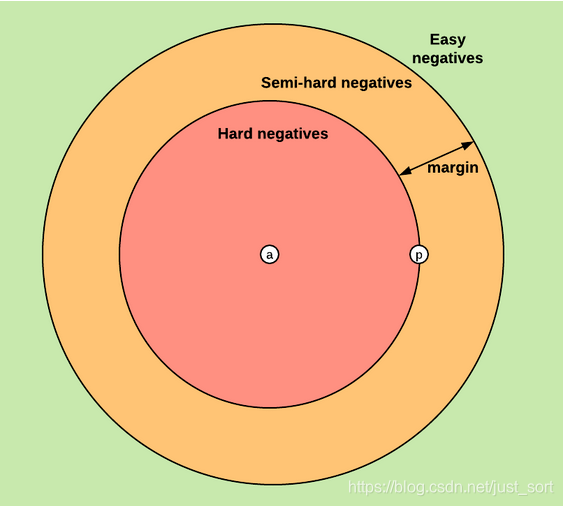
然后FaceNet的训练策略是随机选取semi-hard triplets来进行训练的,当然也可以选择hard triplets或者两者结合来训练。关于FaceNet更多的训练细节我们就不再介绍了,这一节的目的是介绍Triplet Loss,之后在人脸识别专栏再单独写一篇介绍FaceNet训练测试以及网络参数细节的。
代码实现¶
简单提供一个Triplet Loss训练Mnist数据集的Keras代码,工程完整地址见附录:
def triplet_loss(y_true, y_pred):
"""
Triplet Loss的损失函数
"""
anc, pos, neg = y_pred[:, 0:128], y_pred[:, 128:256], y_pred[:, 256:]
# 欧式距离
pos_dist = K.sum(K.square(anc - pos), axis=-1, keepdims=True)
neg_dist = K.sum(K.square(anc - neg), axis=-1, keepdims=True)
basic_loss = pos_dist - neg_dist + TripletModel.MARGIN
loss = K.maximum(basic_loss, 0.0)
print "[INFO] model - triplet_loss shape: %s" % str(loss.shape)
return loss
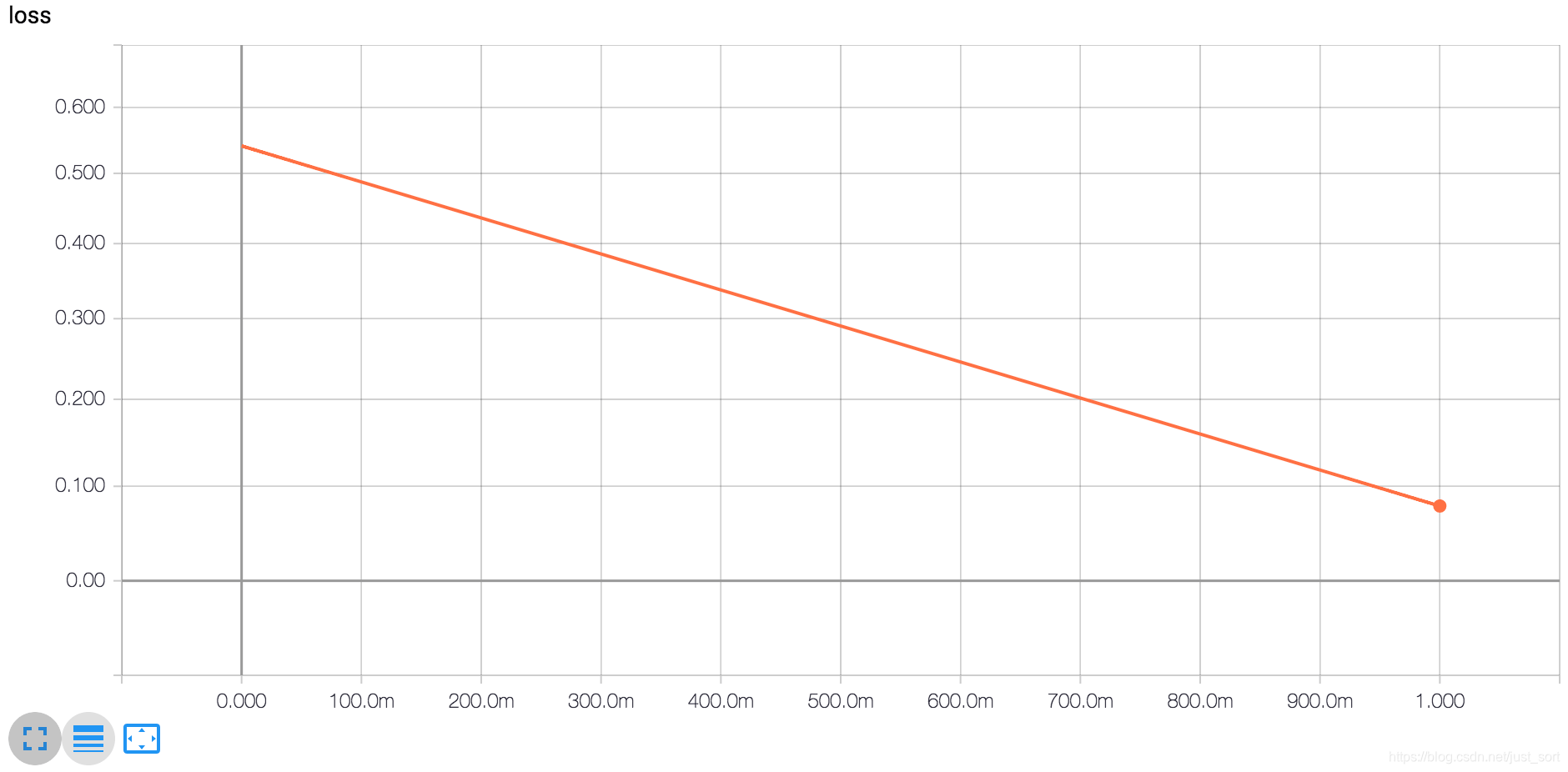
可以来感受一下Triplet Loss训练Mnist时Loss下降效果,几乎是线性下降:
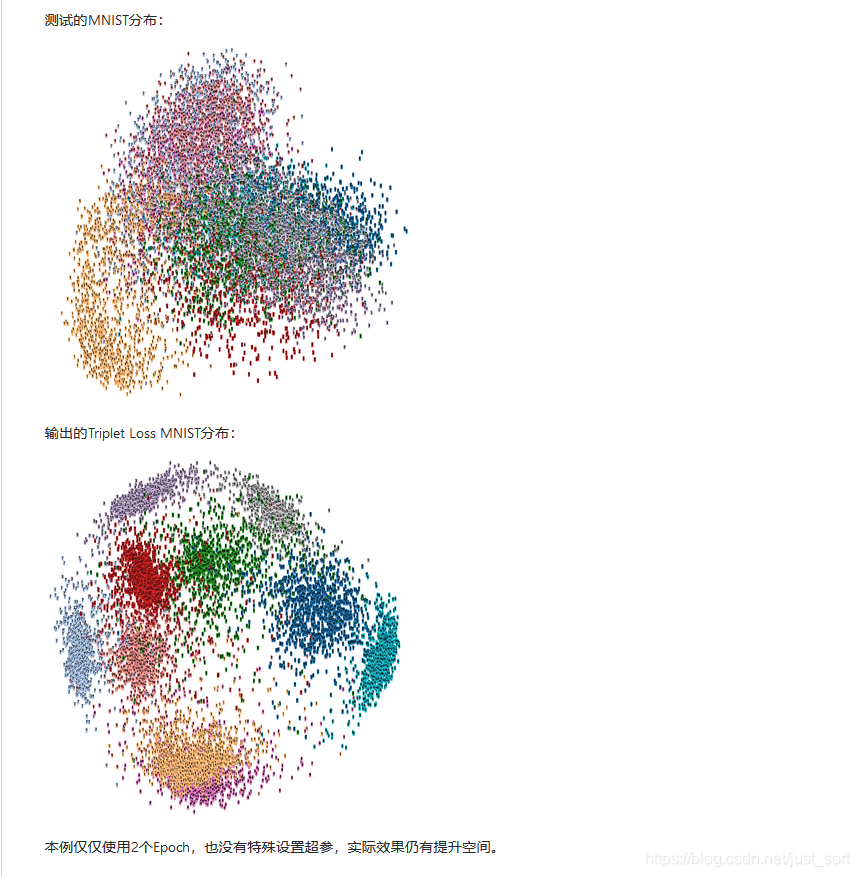
另外看一下作者只跑了2个Epoch之后的降维可视化结果,截图如下,可以看到已经类别已经聚集得特别好了:
附录¶
- Contrasstive Loss原文:http://www.cs.toronto.edu/~hinton/csc2535/readings/hadsell-chopra-lecun-06-1.pdf
- Triplet Loss原文:https://arxiv.org/abs/1503.03832
- 参考:https://zhuanlan.zhihu.com/p/76515370
- Triplet Loss代码实现:https://github.com/SpikeKing/triplet-loss-mnist
推荐阅读¶
- 【损失函数合集】ECCV2016 Center Loss
- 目标检测算法之RetinaNet(引入Focal Loss)
- 目标检测算法之AAAI2019 Oral论文GHM Loss
- 目标检测算法之CVPR2019 GIoU Loss
- 目标检测算法之AAAI 2020 DIoU Loss 已开源(YOLOV3涨近3个点)
欢迎关注GiantPandaCV, 在这里你将看到独家的深度学习分享,坚持原创,每天分享我们学习到的新鲜知识。( • ̀ω•́ )✧
有对文章相关的问题,或者想要加入交流群,欢迎添加BBuf微信:

本文总阅读量次