前言¶

时间来到2015年，何凯明团队提出Residual Networks(ResNet，残差网络)，这个网络横扫了2015年的各类CV比赛。在ImageNet的分类，定位，回归以及COCO的检测，分割比赛中均获得冠军。ResNet的论文地址和作者的源码见附录。

贡献¶

引入残差网络(跳跃连接)，这个残差结构实际上就是一个差分方放大器，使得映射 $F(x)$ 对输出的变化更加敏感。这个结构不仅改善了网络越深越难训练的缺点还加快了模型的收敛速度。

网络结构¶

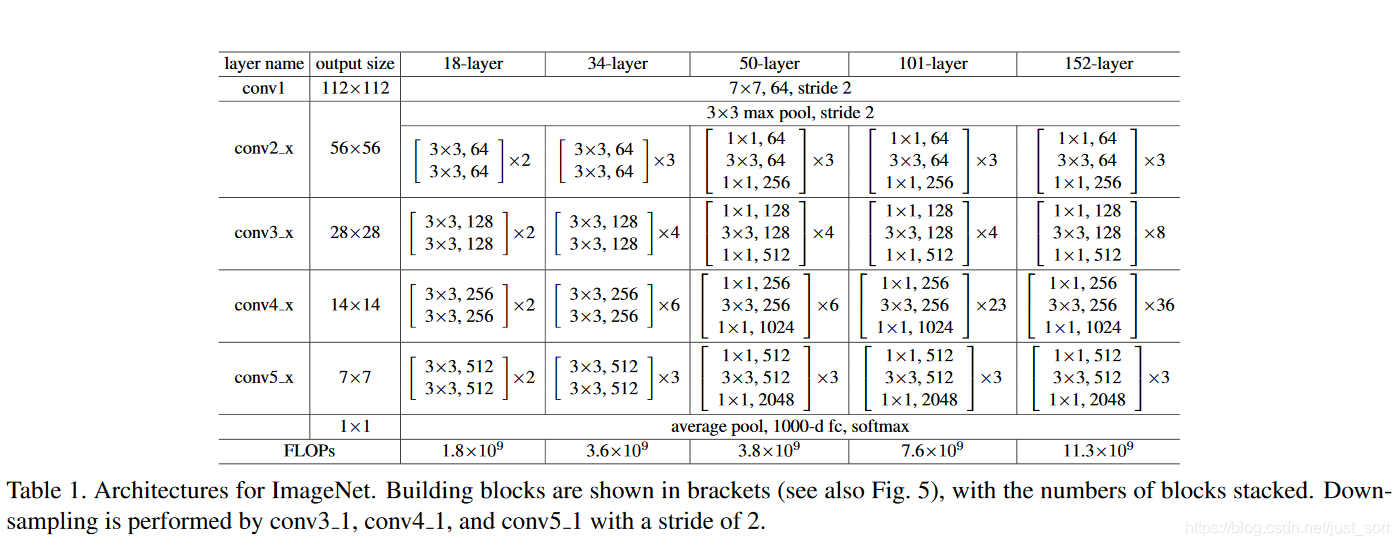
如下表所示，论文设计了18、34、50、101、152五种不同深度的ResNet，用的都是 $1\times 1$ 和 $3\times 3$ 的小卷积核。

在这里插入图片描述

深入理解¶

什么是残差？¶

在ResNet之前普遍认为网络的深度越深，模型的表现就更好，因为CNN越深越能提取到更高级的语义信息。但论文的实验发现，通过和浅层网络一样的方式来构建深层网络，结果性能反而下降了，这是因为网络越深越难训练。实验如Figure1所示：

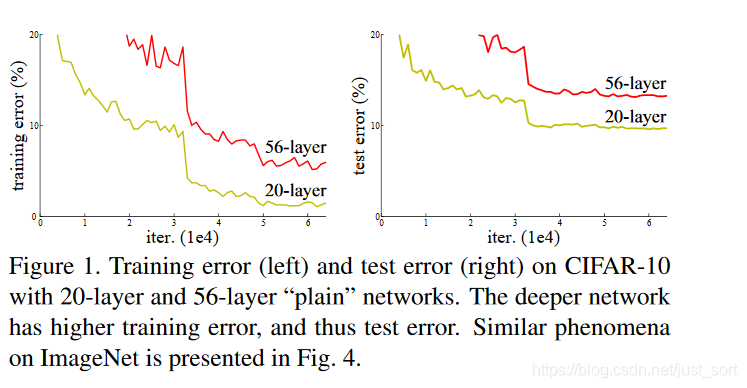
在这里插入图片描述

因此网络的深度不能随意的加深，前面介绍的GoogLeNet和VGG16/19均在加深深度这件事情上动用了大量的技巧。那么到底什么是残差呢？

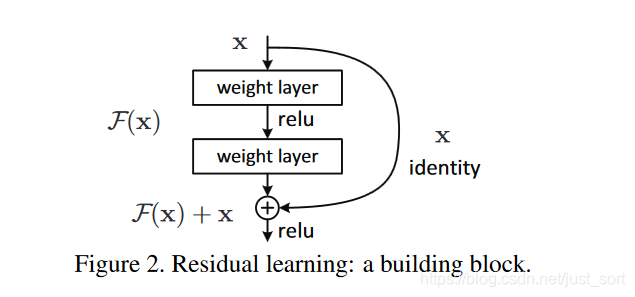
首先，浅层网络都是希望学习到一个恒等映射函数 $H(x)=x$ ，其中 $=$ 指的是用 $H(x)$ 这个特征/函数来代表原始的 $x$ 的信息，但随着网络的加深这个恒等映射变得越来越难以拟合。即是用BN这种技巧存在，在深度足够大的时候网络也会难以学习这个恒等映射关系。因此ResNet提出将网络设计为 $H(x)=F(x)+x$ ，然后就可以转换为学习一个残差函数 $F(x)=H(x)-x$ ，只要残差为 $0$ ，就构成了一个恒等映射 $H(x)=x$ ，并且相对于拟合恒等映射关系，拟合残差更容易。残差结构具体如Figure2所示，identity mapping表示的就是恒等映射，即是将浅层网络的特征复制来和残差构成新的特征。其中恒等映射后面也被叫作跳跃连接(skip connrection)或者短路连接(shortcut connection)，这一说法一直保持到今天。同时我们可以看到一种极端的情况是残差映射为 $0$ ，残差模块就只剩下 $x$ ，相当于什么也不做，这至少不会带来精度损失，这个结构还是比较精巧的。

在这里插入图片描述

残差为什么有效？¶

为什么残差结构是有效的呢？这是因为引入残差之后的特征映射对输出的变化更加敏感，也即是说梯度更加，更容易训练。从图2可以推导一下残差结构的梯度计算公式，假设从浅层到深层的学习特征 $y=x+F(x,W)$ ，其中 $F(x,W)$ 就是带权重的卷积之后的结果，我们可以反向求出损失函数对 $x$ 的提取 $\frac{dloss}{dx}=\frac{dloss}{dy} \times \frac{dy}{dx}=\frac{dloss} { dy} *(1+\frac{dF(x,W)}{dx})$ ，其中 $\frac{dloss}{dy}$ 代表损失函数在最高层的梯度，小括号中的 $1$ 表示残差连接可以无损的传播梯度，而另外一项残差的梯度则需要经过带有可学习参数的卷积层。另外残差梯度不会巧合到全部为 $-1$ ，而且就算它非常小也还有 $1$ 这一项存在，因此梯度会稳定的回传，不用担心梯度消失。同时因为残差一般会比较小，残差学习需要学习的内容少，学习难度也变小，学习就更容易。

ResNet的两种残差单元设计¶

ResNet设计了两种残差单元，如下图所示。

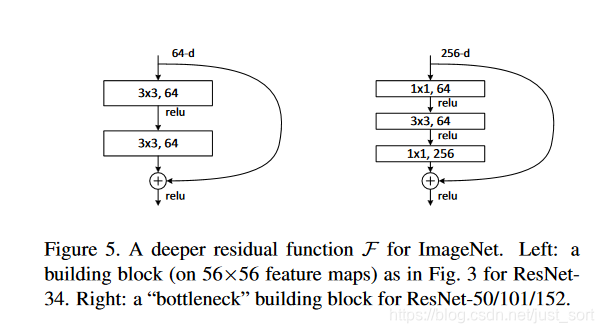
在这里插入图片描述

可以看到左边的残差结构用在浅层的Resnet如Resnet34，而右边的结构用在深层网络如ResNet-50/101/152，同时右边的结构又叫bottleneck，大概翻译是瓶颈结构，这种先降维再做卷积，之后再升维回去的方式也是为了升维但不增加参数数目。

残差连接在维度不匹配时咋办？¶

细心的同学会发现在论文中提供的ResNet34的结构中不仅仅有实线，而且有虚线，如下所示：

在这里插入图片描述

这个实线代表的是维度匹配的shortcut连接，而维度不匹配的用虚线来代替。维度匹配时可以直接用 $F(x)+x$ 来做映射，而维度不匹配的时候要强行让维度匹配或者不要shortcut连接，强行让维度匹配有两种做法：

F(x)+Wx，投影到新的空间，W就是一定数量的1x1卷积核，这种表现稍好，但会增加参数和计算量。
zero padding 增加通道维度法。

至于为什么会存在维度不匹配？因为卷积核的步长为2来做了下采样。

实验¶

验证残差结构的有效性¶

Figure4左图的plain网络是没有用残差结构的，而右图是用了残差结构的ResNet。两个网络都是基于VGG19改造的，并在ImageNet上训练，细线是训练误差，粗线是验证误差。可以看到，随着迭代次数的增加，plain的34层比18层的效果逐渐变差，而ResNet的34层比18层效果显著提升，由此可以证明残差结构是有效的。

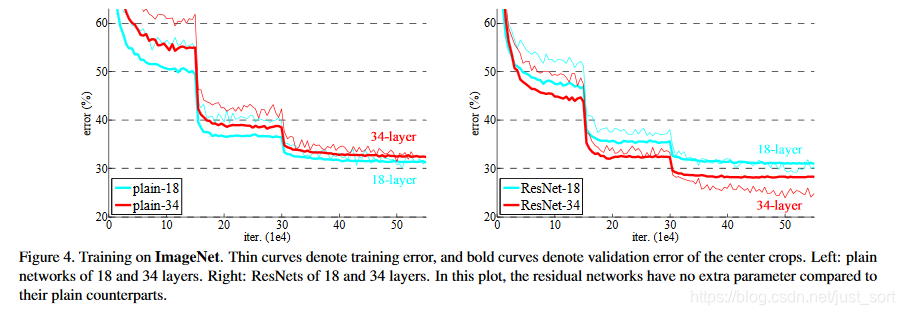
在这里插入图片描述

实验结果¶

和其他SOTA分类网络的对比结果如下：

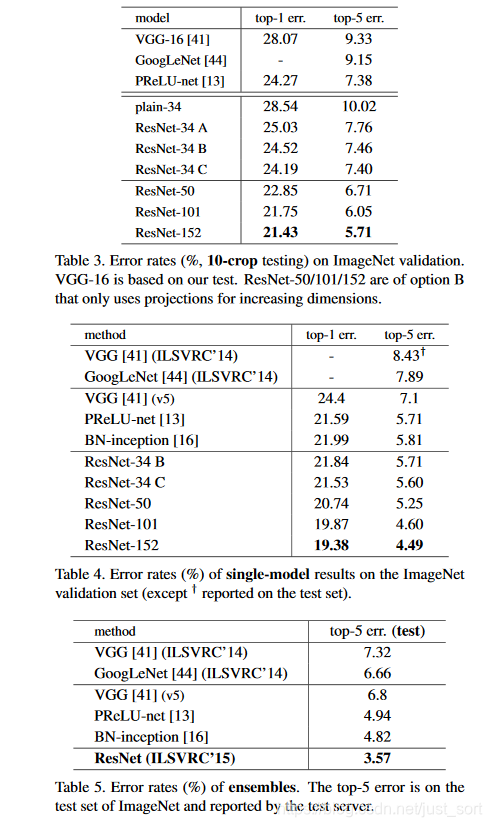
在这里插入图片描述

代码实现¶

看一个ResNet50的Keras代码实现好了。

def Conv2d_BN(x, nb_filter,kernel_size, strides=(1,1), padding='same',name=None):
    if name is not None:
        bn_name = name + '_bn'
        conv_name = name + '_conv'
    else:
        bn_name = None
        conv_name = None

    x = Conv2D(nb_filter,kernel_size,padding=padding,strides=strides,activation='relu',name=conv_name)(x)
    x = BatchNormalization(axis=3,name=bn_name)(x)
    return x

def Conv_Block(inpt,nb_filter,kernel_size,strides=(1,1), with_conv_shortcut=False):
    x = Conv2d_BN(inpt,nb_filter=nb_filter[0],kernel_size=(1,1),strides=strides,padding='same')
    x = Conv2d_BN(x, nb_filter=nb_filter[1], kernel_size=(3,3), padding='same')
    x = Conv2d_BN(x, nb_filter=nb_filter[2], kernel_size=(1,1), padding='same')
    if with_conv_shortcut:
        shortcut = Conv2d_BN(inpt,nb_filter=nb_filter[2],strides=strides,kernel_size=kernel_size)
        x = add([x,shortcut])
        return x
    else:
        x = add([x,inpt])
        return x

def ResNet50():
    inpt = Input(shape=(224,224,3))
    x = ZeroPadding2D((3,3))(inpt)
    x = Conv2d_BN(x,nb_filter=64,kernel_size=(7,7),strides=(2,2),padding='valid')
    x = MaxPooling2D(pool_size=(3,3),strides=(2,2),padding='same')(x)

    x = Conv_Block(x,nb_filter=[64,64,256],kernel_size=(3,3),strides=(1,1),with_conv_shortcut=True)
    x = Conv_Block(x,nb_filter=[64,64,256],kernel_size=(3,3))
    x = Conv_Block(x,nb_filter=[64,64,256],kernel_size=(3,3))

    x = Conv_Block(x,nb_filter=[128,128,512],kernel_size=(3,3),strides=(2,2),with_conv_shortcut=True)
    x = Conv_Block(x,nb_filter=[128,128,512],kernel_size=(3,3))
    x = Conv_Block(x,nb_filter=[128,128,512],kernel_size=(3,3))
    x = Conv_Block(x,nb_filter=[128,128,512],kernel_size=(3,3))

    x = Conv_Block(x,nb_filter=[256,256,1024],kernel_size=(3,3),strides=(2,2),with_conv_shortcut=True)
    x = Conv_Block(x,nb_filter=[256,256,1024],kernel_size=(3,3))
    x = Conv_Block(x,nb_filter=[256,256,1024],kernel_size=(3,3))
    x = Conv_Block(x,nb_filter=[256,256,1024],kernel_size=(3,3))
    x = Conv_Block(x,nb_filter=[256,256,1024],kernel_size=(3,3))
    x = Conv_Block(x,nb_filter=[256,256,1024],kernel_size=(3,3))

    x = Conv_Block(x,nb_filter=[512,512,2048],kernel_size=(3,3),strides=(2,2),with_conv_shortcut=True)
    x = Conv_Block(x,nb_filter=[512,512,2048],kernel_size=(3,3))
    x = Conv_Block(x,nb_filter=[512,512,2048],kernel_size=(3,3))
    x = AveragePooling2D(pool_size=(7,7))(x)
    x = Flatten()(x)
    x = Dense(1000,activation='softmax')(x)

    model = Model(inputs=inpt,outputs=x)
    return model

后记¶

不知不觉卷积神经网络学习路线已经做到第10期了，这个系列我大概会做30期左右，非常感谢大家对GiantPandaCV公众号的支持，希望可以一起学习进步。

附录¶

论文原文：https://arxiv.org/abs/1512.03385
作者源码：https://github.com/KaimingHe/deep-residual-networks
参考：https://zhuanlan.zhihu.com/p/65565361

卷积神经网络学习路线往期文章¶

欢迎关注我的微信公众号GiantPandaCV，期待和你一起交流机器学习，深度学习，图像算法，优化技术，比赛及日常生活等。

图片.png

本文总阅读量次