前言¶

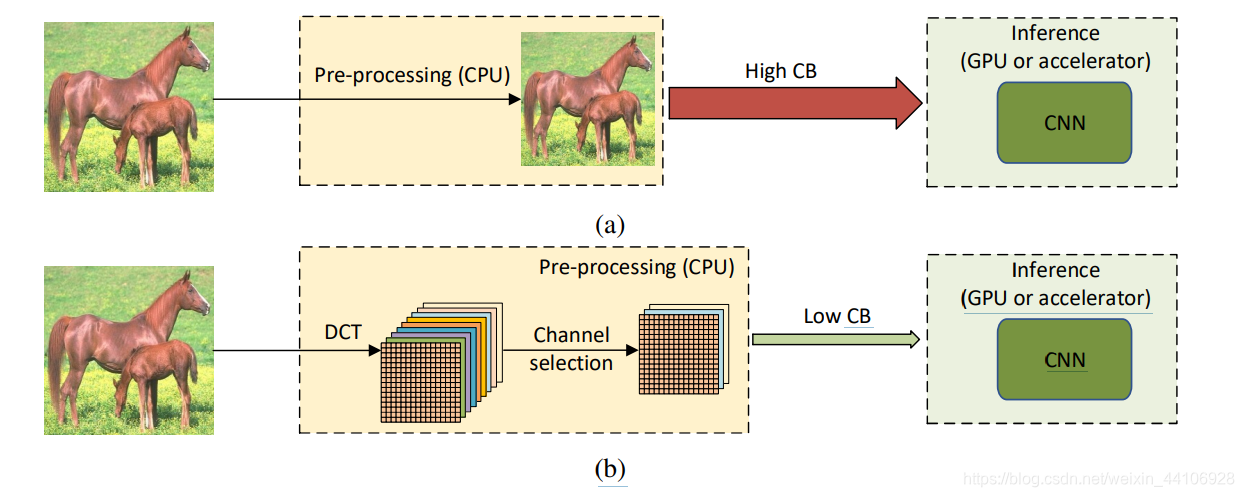
传统的CNN都是在图像的空间域上进行特征学习，受限于显存限制，CNN的输入图像不能太大，最常见的尺寸就是224x224。而常用的预处理(Resize)，以及CNN中的下采样，会比较粗暴的损失数据的信息。阿里达摩院联合亚利桑那州大学提出了基于DCT变换的模型，旨在通过DCT变换保留更多原始图片信息，并减少CPU与GPU的通信带宽，最后的实验也证明该模型的有效性

原始论文地址：Learning in the Frequency Domain 代码地址 DCTNet

介绍¶

大部分CNN模型只能接受 224x224大小的RGB图片，然而现实中存在大量高清图片(1920x1080)，甚至最常用的ImageNet数据集，平均图片大小来到了 482x415。

RGB格式图片大小通常比较大，在CPU和GPU传输需要较大通信带宽，并且难以部署。同时我们预处理里面的缩放以及下采样，会带来信息的损失以及精度的下降。

本文，我们尝试在频域内维持高分辨率的原始图片，进行DCT变换，并通过动/静态的通道选择方法，对输入通道进行蒸馏(最高可蒸馏87.5%在Resnet)，并保持较高精度。

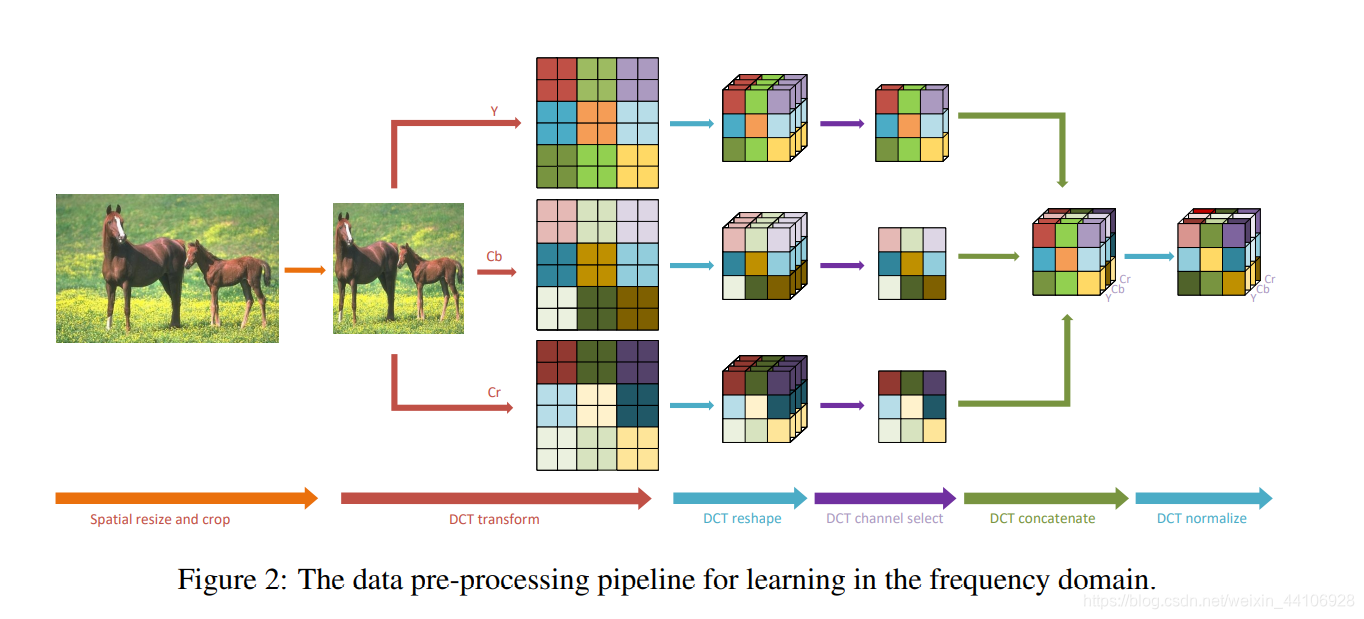
在这里插入图片描述

方法¶

在这里插入图片描述

上图是整个图像处理流程，我们依然在CPU上对图片进行预处理。

首先将RGB格式转化为YCbCr格式
然后做DCT变换转换到频域
然后我们将相同频率的二维DCT变换系数分组到一个通道，形成一个立方体(Cube)。
为了进一步降低推理时间，我们从中选出比较重要的几个通道作为输入。其中方法包含动态选择和静态选择
最后将这些Tensor给连结到一起并归一化。

我们这里遵循JPEG的8x8分块形式，将一张图片分成8x8的小方块，在单独对每个小方块上做DCT变换

然后我们将所有8×8块中相同频率的分量分组到一个通道，保持分块在每个频率上的空间对应关系。

因此 Y，Cb，Cr每个通道都提供了8x8=64的通道。

处理后的图片形状变为

$(H/8,W/8,C*64)$

使用了这种处理方法，意味着在相同开销下，我们的输入图片可以比原始的大8倍！

例如，对于MobileNetv2，我们可以输入896x896x3的图片，处理完后为112x112x192大小，再通过第一个卷积模块对通道数进行调整。

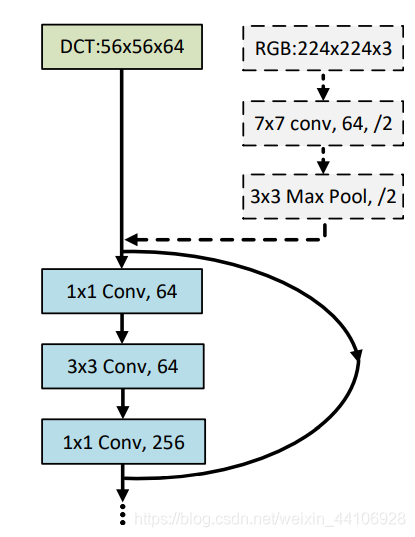
如下图所示，我们将上述DCT处理步骤替换到ResNet中，仅需把前面三个卷积，池化模块（步长为2）给去除即可。其他结构保持不变。

在这里插入图片描述

DCT（补充）¶

具体可以参考详解离散余弦变换（DCT） DCT即离散余弦变换，实际上就是将输入信号限定为实偶信号的离散傅里叶变换(DFT)

公式为

$X[K] = \Sigma_{n=0}^{N-1}X[n]*(cos{\frac{2\pi kn}{N}})$

推广到常规的图像处理中，DCT的计算复杂度还是比较高的，JPG压缩里面就对DCT变换进行了改进，选择对图像分块处理。具体做法是：

先将图像分成8x8的图块
对每一个图块做DCT变换
最后将图块拼接回来

这种分块处理的操作一定程度上提高了DCT变换的效率

动态通道选择¶

考虑到各个频率通道对预测的贡献率，我们设计了一种模块，来动态的选择较为重要的通道，从而达到蒸馏的目的。

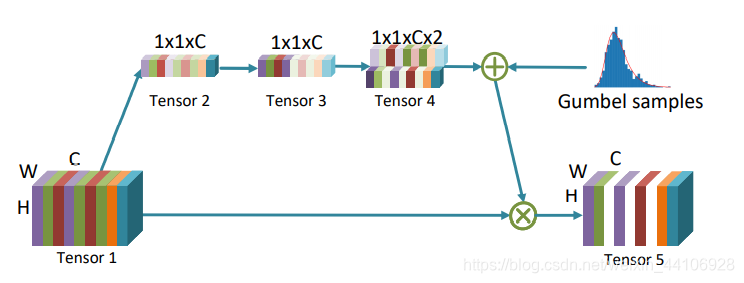
在这里插入图片描述

该模块类似SEBlock，具体处理流程如下

先用全局平均池化层(Global Average Pool)，将Tensor调整到1x1xC的形式，得到Tensor2
使用1x1的卷积核进行计算，得到Tensor3
通过两个可训练参数，对Tensor3进行相乘，得到形状为1x1x2C的Tensor4。这两个训练参数对通道进行采样，比如Tensor4的某个通道的值分别为7.5和2.5，那么代表有75%的概率对应Tensor5的通道输出为0

该模块实际上是一个门控模块(Gate Module)，门控模块的挑战在于，在Tensor4中进行采样这一过程是不可微分的，因此我们转化成Gumbel Softmax的形式

Gumbel Softmax¶

具体可以参考

PyTorch 32.Gumbel-Softmax Trick Gumbel softmax在可微NAS的作用是什么？常规直接采样是无法求导，也缺乏随机性的，我们可以引入一个新的参数 $\epsilon$ ，假定其符合某个分布，即

$\epsilon \in U(0,1)$

我们假设采样对应的概率分布向量是P，做以下操作

$G_i=-log(-log(\epsilon_{i}))$
$Z_{j}= \frac{exp(\frac{log(p_{i})+g_{i}}{\tau})}{\Sigma_{j=1}^{k}exp\frac{log(p_{j})+g_{j}}{\tau})}$

这里的 $\tau$ 是一个超参数，取值越小，最后softmax结果越接近one-hot形式。 通过引入随机变量以及softmax，我们就能巧妙的将采样过程构建成随机且可导了

静态通道选择¶

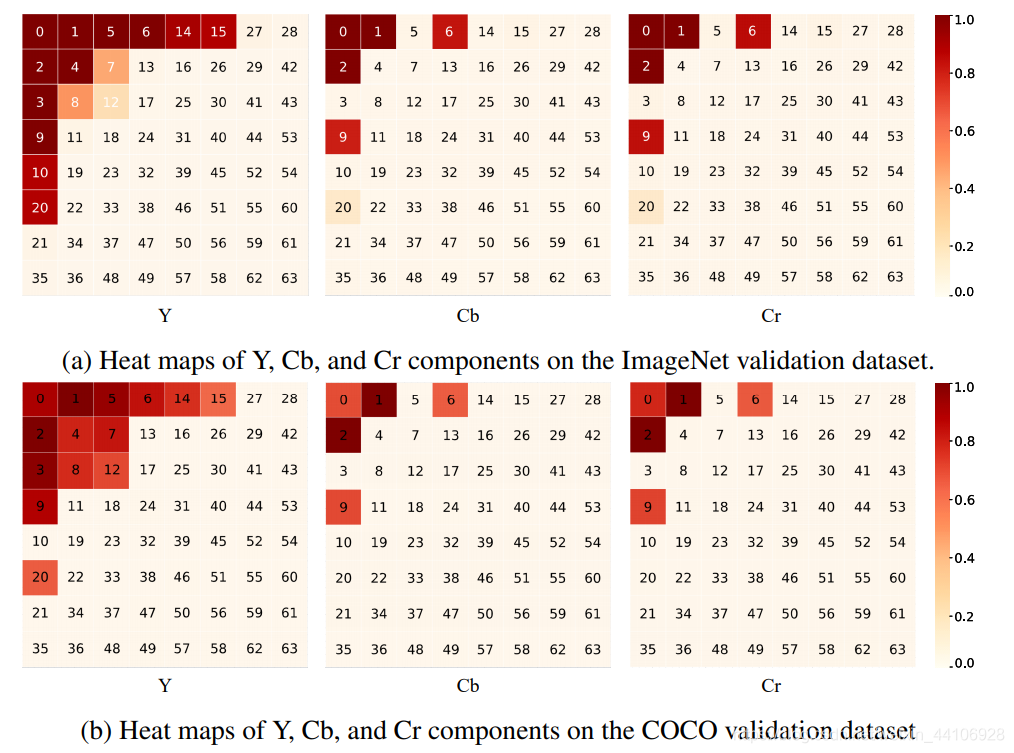
在推理阶段，我们可以使用静态通道选择的方法。我们从统计角度上对CNN感兴趣的通道进行了分析，得出的结论如下 1. 大部分低频通道被选取的频率大于高频通道 2. Y通道对应的内容被选取的频率大于其他两个Cb，Cr通道 3. 通道选取热力图表明，在不同任务比如分类，分割。频率通道被选取的模式是很相似的，这意味着我们的方法能扩大到更复杂的视觉任务上 4. 一些低频通道被选取的频率要稍小于高频通道，比如在Cb，Cr上，6，9被选择的频率要高于5，3。

在这里插入图片描述

最后我们在损失函数中加了一项正则化项用于平衡选择通道的数量，公式为

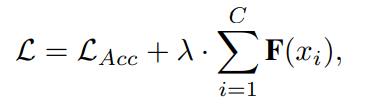
在这里插入图片描述

其中第一项是准确率对应的Loss，第二项则对应选择的通道数

实验部分¶

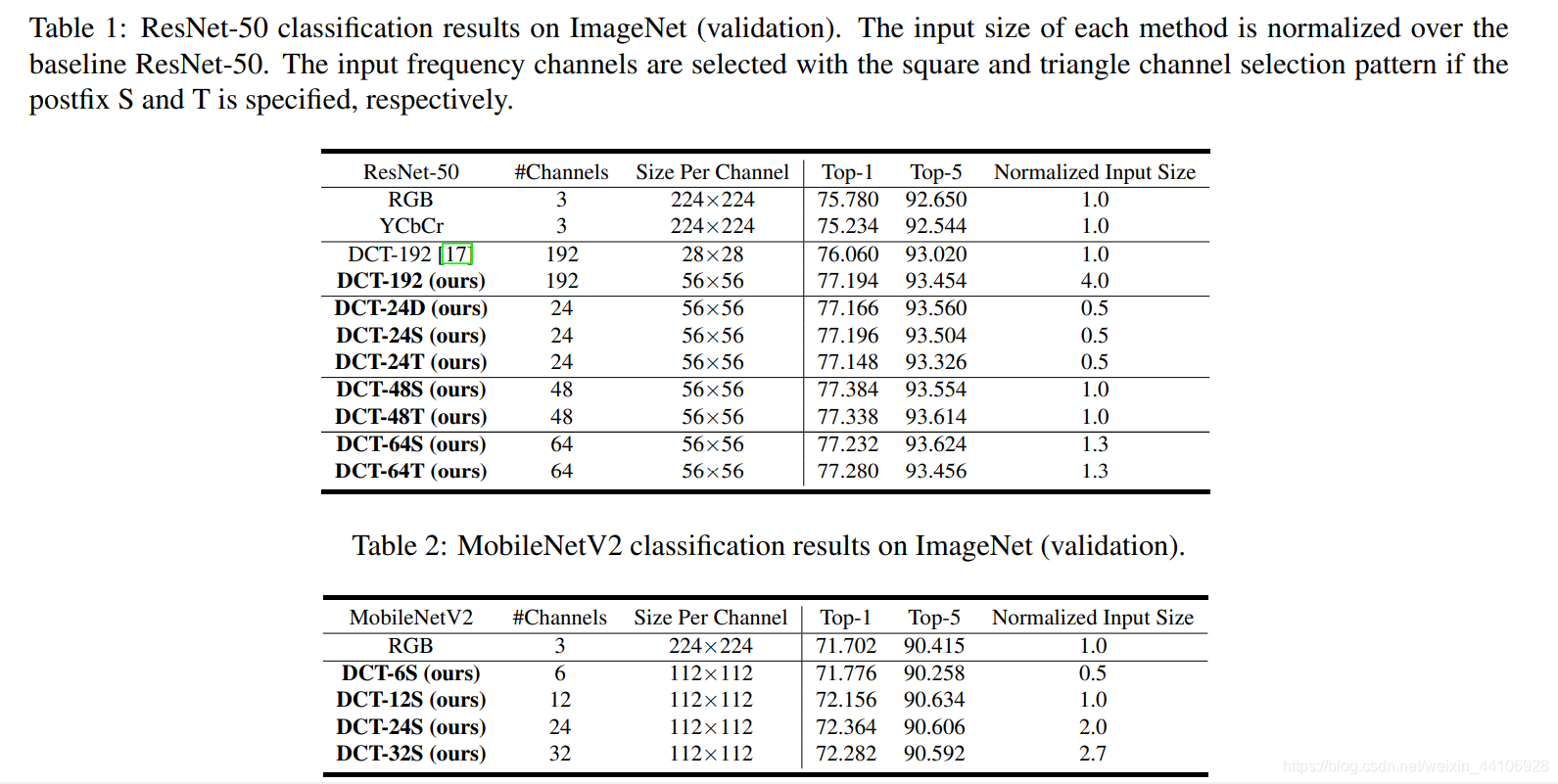
这里就不细讲了，基本上替换常见的模型后都有一定提升

这里的24，48，64就是静态选取通道的结果，也可以很明显看到即使选取通道数较少，准确率也是很高的。

在这里插入图片描述

总结¶

阿里达摩院这一篇论文出发点非常好，作者考虑在频域上重建高分辨率图像，并对通道进行统计，做了通道选择，进一步降低了训练和推理的输入数据量。替换到常用CNN结构中也十分简单，最后的实验也表明了该方法的有效性。

拓展阅读（个人实验）¶

YCbCr转换¶

这里参考的是 RGB与YCBCR颜色空间转换及python实现

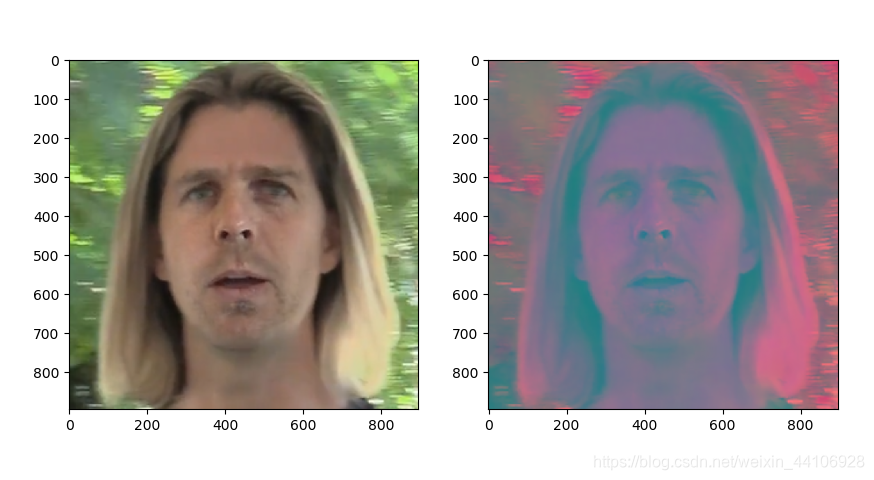
其中RGB转换成YCbCr只需要通过一个矩阵运算

在这里插入图片描述

效果如下

在这里插入图片描述

分块DCT实验¶

这里输入图片大小为224x224x3，以8x8分块进行DCT变换，然后将8x8的系数展开成64大小的张量。

原本输入到DCT的图片（3个通道每一个通道单独输入进去）维度是

$shape=(224,224,1)$

经过变换，展开得到

$shape=(28,28,64)$

最后分别将三个通道的结果，添加到一个list

示例代码如下

import numpy as np
import cv2
import matplotlib.pyplot as plt


def rgb2ycbcr(rgb_image):
    rgb_image = rgb_image.astype(np.float32)
    # 1：创建变换矩阵，和偏移量
    transform_matrix = np.array([[0.257, 0.564, 0.098],
                                 [-0.148, -0.291, 0.439],
                                 [0.439, -0.368, -0.071]])
    shift_matrix = np.array([16, 128, 128])
    ycbcr_image = np.zeros(shape=rgb_image.shape)
    w, h, _ = rgb_image.shape
    # 2：遍历每个像素点的三个通道进行变换
    for i in range(w):
        for j in range(h):
            ycbcr_image[i, j, :] = np.dot(transform_matrix, rgb_image[i, j, :]) + shift_matrix
    return ycbcr_image


img = cv2.imread('./1.png')
img = rgb2ycbcr(img)
img = cv2.resize(img, (224, 224))

dct_list = []
dct_mat = []

for index in range(3):
    img_perchannel = np.float32(img[:, :, index])
    dct = np.zeros_like(img_perchannel)
    dct_matrix = np.zeros(shape=(28, 28, 64))
    for i in range(0, img_perchannel.shape[0], 8):
        for j in range(0, img_perchannel.shape[1], 8):
            dct[i:(i + 8), j:(j + 8)] = np.log(np.abs(cv2.dct(img_perchannel[i:(i + 8), j:(j + 8)])))
            dct_matrix[i // 8, j // 8, :] = dct[i:(i + 8), j:(j + 8)].flatten()

    dct_list.append(dct)
    dct_mat.append(dct_matrix)


img_num = 9
for i in range(img_num):
    img = dct_mat[0][:, :, i] # 这里只展示Y通道dct变换出来的图片
    plt.subplot(img_num // 3, 3, i + 1)
    plt.imshow(img)

plt.show()

下图分别是Y，Cb，Cr三通道对应的DCT图，这里只打印了前9张。

实际上每个通道经过上述处理后，有64张图，即 (28, 28, 64)

Y通道图¶

在这里插入图片描述

Cb通道图¶

在这里插入图片描述

Cr通道图¶

在这里插入图片描述

前言¶

介绍¶

方法¶

DCT（补充）¶

动态通道选择¶

Gumbel Softmax¶

静态通道选择¶

实验部分¶

总结¶

拓展阅读（个人实验）¶

YCbCr转换¶

分块DCT实验¶

Y通道图¶

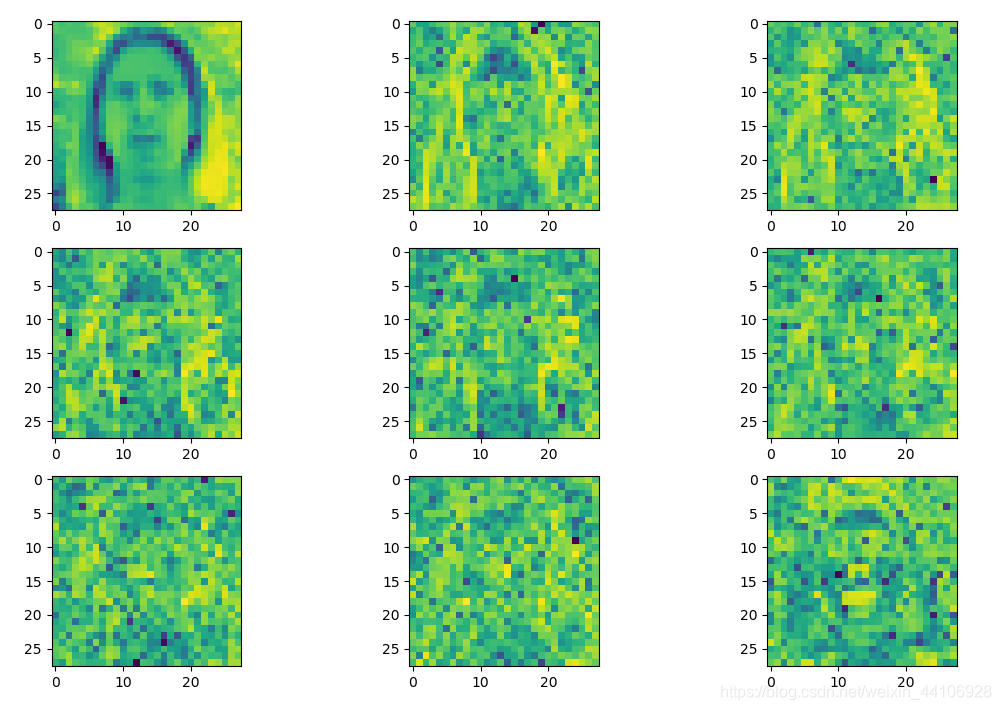
Cb通道图¶

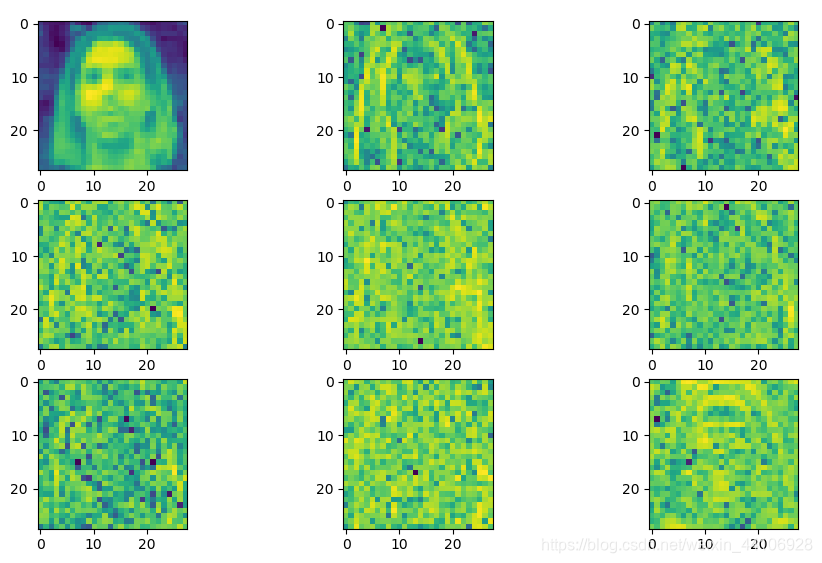
Cr通道图¶

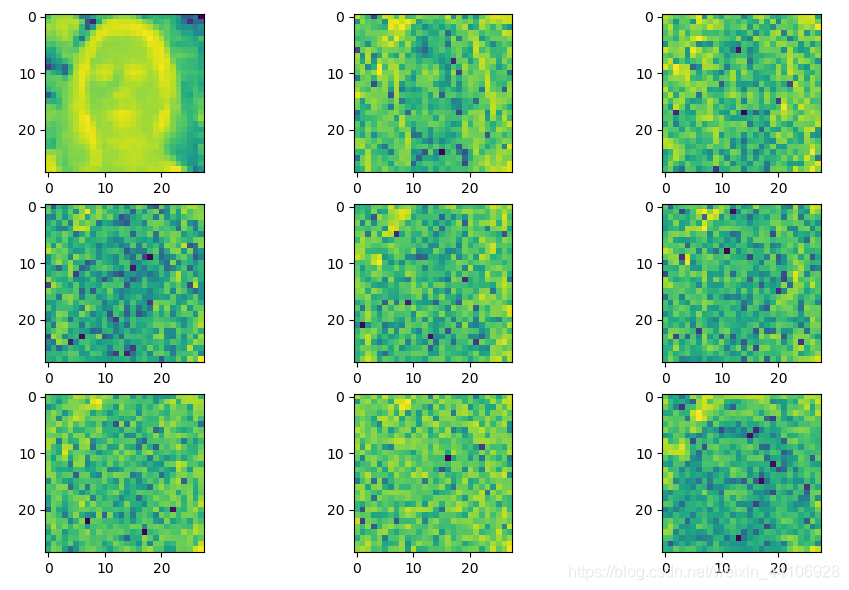
相关资料¶