优化与深度学习之间的关系¶

在深度学习任务中，我们常常会为模型定义一个损失函数，损失函数表征的是预测值和实际值之间的差距，再通过一定的优化算法减小这个差距

然后绝大多数情况下，我们的损失函数十分复杂，不像我们解数学题能得到一个确定，唯一的解析解。而是通过数学的方法去逼近一个解，也称数值解

局部最小值和全局最小值¶

假设我们的损失函数是

$f(x) = x*cos(\pi*x)$

import matplotlib.pyplot as plt
import numpy as np

x = np.arange(-2, 2, 0.01)
print(x)
f = x*np.cos(np.pi*x)
plt.plot(x, f)
plt.show()

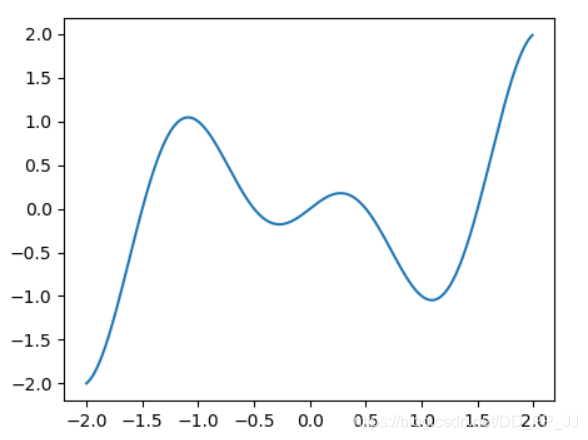
我只画出了区间(-2, 2)的函数图像，通过观察图像，我们发现该函数有两个波谷，分别是局部最小值和全局最小值。

到达局部最小值的时候，由损失函数求得的梯度接近于0，我们很难再跳出这个局部最小值，进而优化到全局最小值，即x=1处，这也是损失函数其中的挑战

鞍点¶

假设我们的损失函数为

$f(x) = x^3$

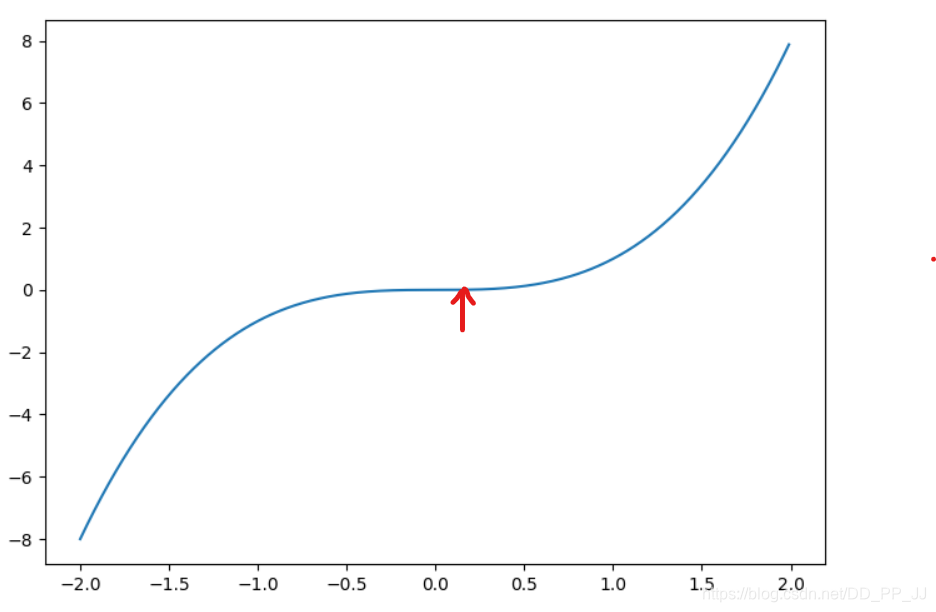
文章所标的点，即是鞍点（saddle point)，形状像马鞍处。

它的特点也是两边的梯度趋近于0，但并不是真正的最小值点

在深度学习优化过程中，这两种情况很常见，我们需要尽可能地通过数学方式去逼近最优

梯度下降为什么有效¶

这里需要用到高数里面的泰勒展开公式

$f(x+\epsilon) = f(x) + \epsilon*f(x)'$

其中

$f(x)'代表x处的梯度$

由于ε是个极小值，所以我们可以用梯度乘上一个很小的数，去替代

$令\epsilon = -n*f(x)’$

$f(x-n*f(x)’) = f(x)-n*f(x)'^2$

由于梯度的平方是恒大于0的，因此有

$f(x - n*f(x)') < f(x)$

看到这里大家应该就明白了，其中n代表的是超参数学习率，我们通过让x减去一个常数乘以学习率，使得目标损失函数值得到下降

接下来我会以函数

$f(x) = x*cos(\pi*x)$

作为一个梯度下降例子

以下是我的画图代码

import matplotlib.pyplot as plt
import numpy as np

def gradient_optimizer(eta):
    x = 0.5
    results = [x]
    for i in range(5):
        # 函数x*np.cos(np.pi*x)的导数为np.cos(np.pi * x) - x * np.sin(np.pi * x)
        x -= eta * (np.cos(np.pi * x) - x * np.sin(np.pi * x))
        results.append(x)
    return results


res = gradient_optimizer(0.1)


def fx(arr):
    ans = []
    for num in arr:
        ans.append(num * np.cos(np.pi * num))
    return ans


def plot():
    x = np.arange(-2, 2, 0.01)
    y = x * np.cos(np.pi * x)
    res_y = fx(res)
    plt.plot(x, y)
    plt.plot(res, res_y, '-o')
    plt.show()


plot()

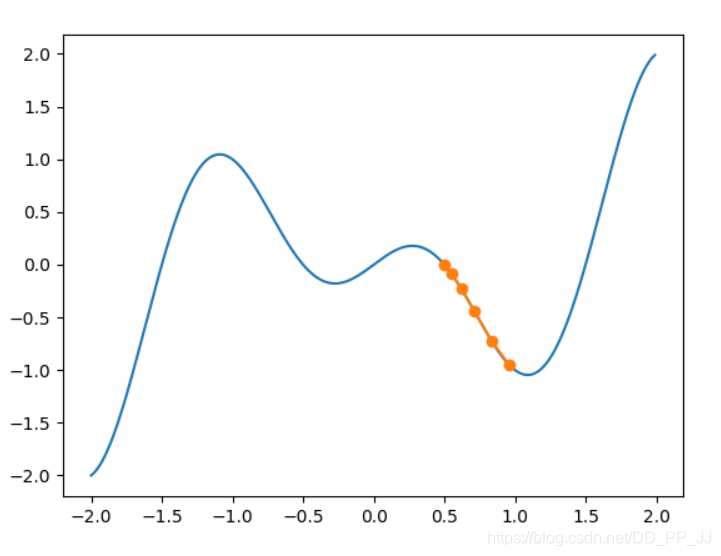
函数从x=0.5开始，很顺利的优化到了全局最小值的地方

那么我们换到x = -1.0，并增加迭代步伐，再次观察梯度下降情况

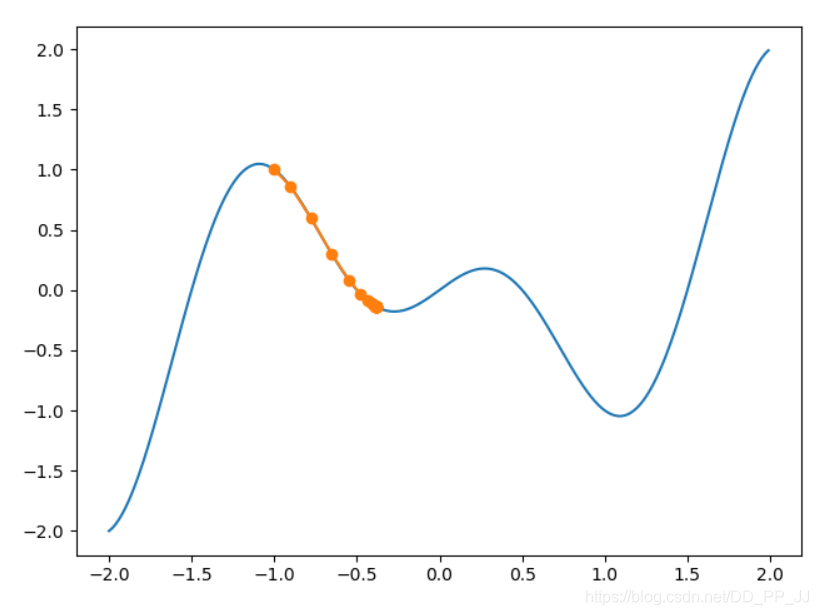
我们将迭代步伐调至20，可见我们卡在局部最小值，无法跳出

那么我们试试增大学习率，看能不能跳出来

我将eta设置为1.000542（PS:。。这个函数太刁钻了，调了半天学习率才达到想要的结果）

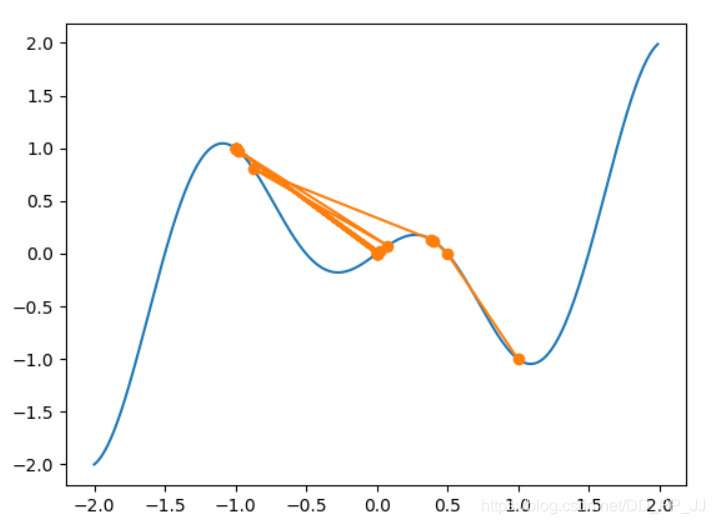
可以看见再经历过一系列震荡后，我们的函数成功到达了全局最小值点，当然背后是我找这个参数的心酸。

我们再把学习率参数调大一点点，将eta设置为1.0055

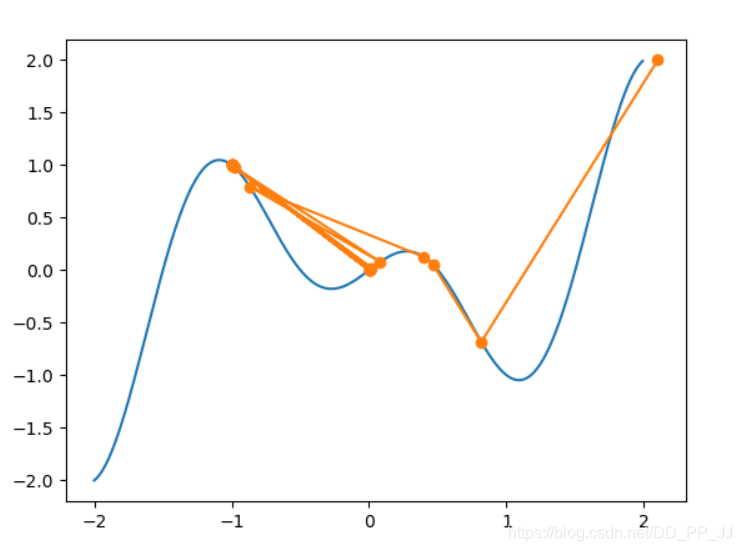
这里我们也可以看得出学习率的关系

当学习率很小，我们下降较为平滑，但容易卡在局部最小值点

当学习率很大，我们梯度优化过程中会十分剧烈，可能达到全局最小值点，但也很可能距离优化目标越来越远

随机梯度下降SGD¶

假设我们有n个样本数据，那么每次进行梯度下降，我们需要分别对每个数据计算其梯度。

时间复杂度为O(n)，当样本很多的时候，这个计算开销是非常大的。

随机梯度下降则是在梯度下降每次迭代当中，随机采取一个样本，计算其梯度，作为整体梯度进行下降，我们的计算开销也就下降到了O(1)

为了梯度值更稳定，我们也可以选择小批量随机梯度下降，以一小批样本的梯度作为整体的梯度估计

动量法Momentum¶

我们实际优化的函数会十分复杂，最常见的函数是多维的情况。当函数在某个方向上变化十分剧烈，则对应方向上的梯度变化也十分剧烈，为了达到收敛，需要更多时间步迭代。

梯度变化剧烈的另外一个原因是，我们单一地考虑了当前的梯度，而忽略了以前的梯度情况。

当我们把以前的梯度加入到当前梯度计算中，会缓解这种问题，加速收敛

动量法引入了一个速度变量，初始化为0，由以下两个公式进行变量维护

$v_t = \gamma*v_{t-1} + \eta_t*g_t \\ x_t = x_{t-1} - v_t$

指数移动平均¶

这里参考的是mxnet出品的动手学教程

我们假设有下面公式

$y{t} = (1-\gamma)*x_t + \gamma*y_{t-1}$

继续展开得到

$y_t = (1-\gamma)*x_t + (1-\gamma)*\gamma*x_{t-1} + \gamma^2*y_{t-2}\\ y_t = (1-\gamma)*x_t + (1-\gamma)*\gamma*x_{t-1} + (1-\gamma)*\gamma^2*x_{t-2} + \gamma^3*y_{t-2}\\ 令 n = \frac{1} {(1-\gamma)}\\ 则 (1-1/n)^n = \gamma^{1/(1-\gamma)} 这里直接是变量替换\\ 而我们由高数的常见的极限公式可得\\ lim_{n \to \infty}(1- \frac{1}{n})^n = \frac{1}{e} = 0.37 \\ 而\gamma \rightarrow 1，则 n \rightarrow \infty \\ 举个例子，取\gamma = 0.9，则根据前面的极限公式 0.9^{10} \rightarrow 0.37 \\ 如果我们把0.37看作是个很小的数，那我们可以忽略了更高阶的系数，比如0.9^{11}, 0.9^{12}等等\\ 换句话说，当\gamma = 0.9，我们只关注近十个阶数的系数$

简单来说，指数移动平均就是计算近几个时间步的加权平均，时间越近，对应的权重就越大

接下来我们对动量法的速度变量进行变形

$v_t = (1-\gamma)*(\frac{\eta}{1-\gamma}*g_t) + \gamma*v_{t-1}$

我们相当于是对

$(\frac{\eta}{1-\gamma}*g_t)$

这一项做了移动平均。因此动量法能综合考虑一定量时间步内的梯度情况

AdaGrad算法¶

在前面两种优化算法里，自变量的每一个元素都是使用同一学习率来自我迭代。

而在前面我们对学习率讨论中，不同学习率所带来的优化效果也不同。

因此我们在思考能否提出一个自适应学习率调整的优化算法

AdaGrad算法维护一个状态变量

通过以下两个公式进行迭代更新

$s_t = s_{t-1} + g_t \odot g_t \\ x_t = x_{t-1} + \frac{\eta} {\sqrt{s_t + \epsilon}} \odot g_t \\ \epsilon 是一个很小的值，防止除0$

我们可以看到状态变量S每次都是通过梯度按元素平方进行迭代，这样每个变量就有自己特定的学习率，而且状态变量放置在分母下，能逐步调小学习率，不需要人为进行调整。

缺点就是可能模型还未收敛，学习率已经过小，很难找到合适的数值解

RMSProp算法¶

既然AdaGrad缺点是因为平方函数是个递增函数，一直迭代会让学习率持续下降。

那么我们不妨将动量法的移动平均思想，用于处理状态变量s

因此RMSProp算是结合了Adagrad和Momentum的思想

计算公式如下

$s_t = \gamma*s_{t-1} +(1-\gamma) * g_t \odot g_t \\ x_t = x_{t-1} + \frac{\eta} {\sqrt{s_t + \epsilon}} \odot g_t \\ \epsilon 是一个很小的值，防止除0$

移动平均并不是一个单调递增的函数，因此它能更好地调节学习率

Adam算法¶

Adam算法则是结合了RMSProp和Momentum算法

它在RMSProp算法基础上也对梯度变量做了指数加权移动平均

公式如下

$v_t = \beta_1*v_{t-1} + (1-\beta_1)*g_t \\ s_t = \beta_2*s_{t-1} + (1-\beta_2)* g_t \odot g_t$

这里对速度变量做的指数移动平均与动量法的方法有点区别

在t较小的时候，各个时间步权值之和不为1

$当\beta_1 = 0.9 \\ v1 = 0.1*g_t$

因此需要做个偏差修正

$v_t = \frac {v_t}{1-\beta1} \\ s_t = \frac {s_t}{1-\beta2} \\$

然后调整每个元素的学习率

$g_t' = \frac{\eta*v_t}{\sqrt{s_t}+\epsilon} 这里\epsilon是一个很小的数 \\ x_t = x_{t-1} - g_t'$

本文总阅读量次