Rethinking and Improving the Robustness of Image Style Transfer¶

图像风格化鲁棒性的再思考和提升¶

Paper Link：https://link.zhihu.com/?target=https%3A//openaccess.thecvf.com/content/CVPR2021/supplemental/Wang_Rethinking_and_Improving_CVPR_2021_supplemental.pdf

Paper Author: Pei Wang;Yijun Li;Nuno Vasconcelos

知乎/github：Owen718

总结写在前面¶

我们知道风格迁移模型中常用预训练VGG模型作为风格迁移损失的提取器，不知道大家有没有想过为什么是VGG?VGG已经很“老”了，和今天大量的新backbone，如我们常用的ResNet相比，VGG实在不算出众。但大量的实验证明，VGG在风格迁移任务上表现的非常出色，并且，随机权重的VGG，也可以有着不错的迁移效果。关于随机权重VGG应用于风格迁移任务，已经有人研究过了。我们反观更热门的ResNet，其效果对比图如下图所示（ $p-$ 表示预训练， $r-$ 表示随机权重），ResNet的效果非常的差。

风格迁移效果对比图，图片来自论文

知乎上也有曾探讨这个问题的帖子，但并没有提到问题的本质，大多是猜测和推理。这篇CVPR21 Oral的论文则深入探究了这一问题，并给出了问题的答案和一个简单而有效的解决方案：

产生这一问题的原因：Residual Connections
许多残差连接导致的结果：残差连接将生成小熵的特征图(“produce feature maps of small entropy”)。
解决方案：通过基于 $Softmax$ 的平滑变换，去平滑所有激活，从而避免低熵的峰值激活。

以下具体解读论文的重点部分内容。

为什么残差连接反而引起了迁移任务上性能的退化？¶

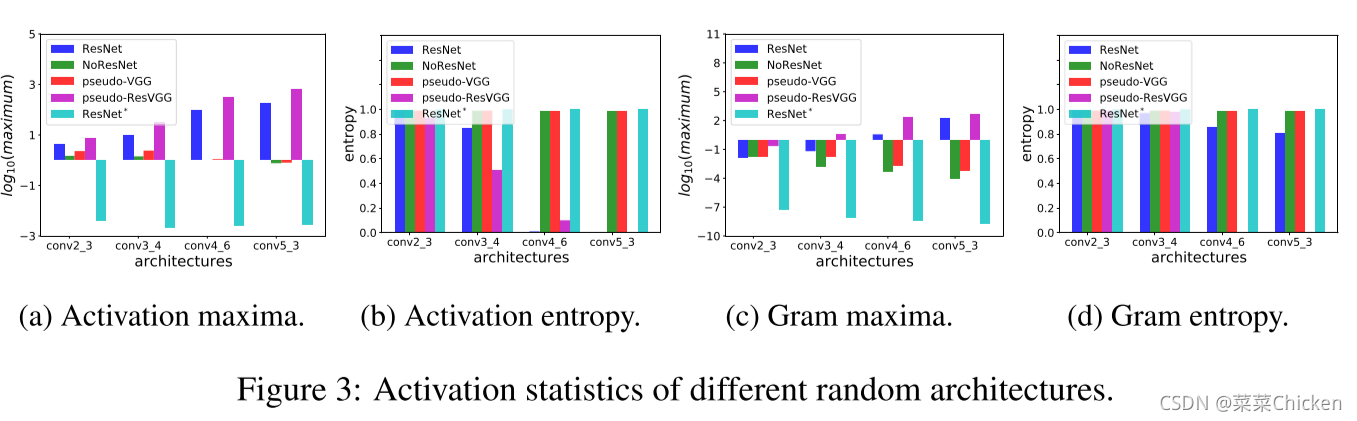
统计对比实验的结果图，图片来自论文

作者做了一系列针对特定层特征的统计对比实验，如图中所示。图中的层就是用来计算 $Content loss$ 和 $Style loss$ 的那些层,其中的ResNet就是普通标准配置的ResNet，NoResNet是不带残差连接的ResNet，pseudo-VGG是作者改造的、层数更深的VGG，pseudo-ResVGG是带残差的、更深的VGG，带星号的，则是使用了作者提出的 $Stylization With Activation smoothinG$ (SWAG)技术。我们可以总结出以下几点原因：

Peaky maximum:图（a）中可以看到，图中带残差连接的模型，随着网络层数的加深，maximum值也在不断加大，而反观不带残差的普通VGG等，其值不断减小。
Small entropy：图（b）中可以看到，不使用SWAG的话，带残差的模型，随着网络层数的加深，熵值急剧减小。
对Gram maxima和Gram entropy而言，也有类似的结论。可参考图c和d。针对这一现象，作者给出了两种可能的解释。

两种可能的解释¶

L2 loss的离群值敏感性¶

让我们回顾一下 $Style loss$ :

$\mathcal{L}_{\text {style }}\left(\mathbf{x}_{0}^{s}, \mathbf{x}\right)=\sum_{l=1}^{L} \frac{w_{l}}{4 D_{l}^{2} M_{l}^{2}}\left\|G^{l}\left(F^{l}(\mathbf{x})\right)-G^{l}\left(F^{l}\left(\mathbf{x}_{0}^{s}\right)\right)\right\|_{2}^{2}$

可以看到，使用了L2 loss，L2损失有一个特点，即其对离群值有着敏感性。当导出的 $Gram$ 矩阵为"峰值"（低熵）时，优化将集中于那些峰值上，而较少关注那些其余的值，也就是说， $Gram$ 矩阵峰值确定了通道维度上高度相关的强激活位置，因此导致了对一些风格样式过度优化（overfit)，却忽略了其余大部分的风格样式。带残差的model无法捕获纹理和风格感知所需的远距离相关特征。

知识蒸馏角度理解——成对的高熵更易学习¶

让我们将风格迁移这一优化过程看成是一种知识提炼的过程：

$\mathcal{L}_{\text {style }}\left(\mathbf{x}_{0}^{s}, \mathbf{x}\right)=\sum_{l=1}^{L} \frac{w_{l}}{4 D_{l}^{2} M_{l}^{2}}\left\|G^{l}\left(F^{l}(\mathbf{x})\right)-G^{l}\left(F^{l}\left(\mathbf{x}_{0}^{s}\right)\right)\right\|_{2}^{2}$

$L_{style}$ 中的 $G^l(F(^l(x)))$ 可以看作是学生网络， $G^l(F(^l(x_0^s)))$ 可以看作是教师网络。

如果接触过蒸馏的话，应该会知道，Soft features相比于Hard features更易被优化。这是因为高熵的教师模型，其输出分布在训练期间产生的梯度变化更小，自然就更易于学习。同样的道理，既然我们已经知道了带残差的model，输出的features，熵是小的，那么我们就可以使用类似于蒸馏中的 $Softmax$ 方法去“软化”特征。也就是后面即将提到的，作者提出的 $SWAG$ 技术，其实就是让训练期间的梯度变化更小、更易学习。

那么，为什么残差连接会导致 Peaky maximum？¶

让我们看一下paper中给出的结构图：

带残差的结构示意图，图片来自原论文

首先，上一级的输出是经过 $ReLU$ 的，是恒正的输出，而BN后的残差连接，将使得maximum的feature部分更“Peaky”， $ReLU$ 恒正，这也导致最小值很可能永远是0，或逼近0，而最大值却不断在变大,而BN并不能有效的降低当前features中的那些maximum，maximum一级一级越来越大，也就导致maximum越来越Peaky了。

Stylization With Activation smoothinG(SWAG)¶

解决方案其实也非常简单，前文其实已经说过了。作者提出使用基于 $Softmax$ 的平滑变换来平滑所有激活，从而避免熵的峰值激活即可：

$\sigma\left(F_{i k}^{l}(\mathbf{x})\right)=\frac{e^{F_{i k}^{l}(\mathbf{x})}}{\sum_{m, n} e^{F_{m n}^{l}(\mathbf{x})}}$

我们来看一下使用SWAG后的两个损失函数：

$\mathcal{L}_{\text {content }}\left(\mathbf{x}_{0}^{c}, \mathbf{x}\right)=\frac{1}{2}\left\|\sigma\left(F^{l}(\mathbf{x})\right)-\sigma\left(F^{l}\left(\mathbf{x}_{0}^{c}\right)\right)\right\|_{2}^{2}$

$\begin{aligned} \mathcal{L}_{\text {style }}\left(\mathbf{x}_{0}^{s}, \mathbf{x}\right)=& \sum_{l}^{L} \frac{w_{l}}{4 D_{l}^{2} M_{l}^{2}} \| G^{l}\left(\sigma\left(F^{l}(\mathbf{x})\right)\right) \\ &-G^{l}\left(\sigma\left(F^{l}\left(\mathbf{x}_{0}^{s}\right)\right) \|_{2}^{2}\right. \end{aligned}$

作者在paper中还有一些效果对比图，挺有意思，大家可以去看一看。

总结¶

这篇Paper其实挺好理解的，给出的解决方案也非常简单，但作者对于实验现象的逐步归纳和分析与扎实的领域功底，非常值得学习，也消除了我之前的一些困惑。

本文总阅读量次