基于模型驱动的单图像去雨深度神经网络¶

A Model-driven Deep Neural Network for Single Image Rain Removal

paper link:https://openaccess.thecvf.com/content_CVPR_2020/papers/Wang_A_Model-Driven_Deep_Neural_Network_for_Single_Image_Rain_Removal_CVPR_2020_paper.pdf

github link:https://github.com/hongwang01/RCDNet

Background¶

深度学习技术在单图去雨任务上取得了很好的性能，但是并没有足够的课解释性，且并没有很好的结合雨条纹的特征（连续、形状相似），针对这些问题，作者提出了一种模型驱动的网络。
一张雨图中重复出现的雨条纹在局部上有着相似的特征：例如形状、粗细、位置。因此可以利用这一先验来恢复图像，即问题转变成从这些局部的类似退化中估计出rainy kernel。虽然中特定的场景中（说白了就是合成数据集），这种依赖于客观先验的假设相当work，但是在真实场景中，这种方法并不适应复杂、多样的雨条纹。因此作者提出将rain layer做一个分解，核心思路就是rain layer分解为雨核和雨图，rain layer可以由二者卷积而成。

Method¶

对于一张雨图，其形成可描述为：

$O=B+R$

其中 $B$ 代表背景层， $R$ 代表雨层。大部分深度学习算法直接学习 $O$ 到 $B$ 的映射或 $O$ 到 $R$ 的映射。

作者提出，雨层其实可以表示为雨核集合与雨图局部重复图（ $M_n$ ）的卷积：

$R^c = \sum^N_{n=1}{C_n^c \otimes M_n,c=1,2,3}$

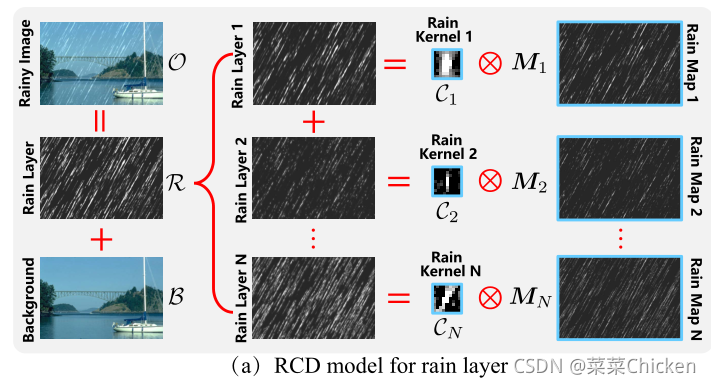
分解示意图，图片来自原论文

因此，式 $O=B+R$ 可以重写为：

$O = B+\sum^N_{n=1}{C_n \otimes M_n}$

因此，可以用卷积集合（paper原文中描述为：convolutional dictionary),来表示雨条纹重复和类似的局部模式，数量不多的核就可以很好的表示多种的雨条纹退化模式，这些核可以从大量的数据中学习得来。与雨核不同，雨图必须随输入的雨量图像而变化，因为雨条纹的位置和偏移是完全随机的。因此，为了得到干净的输出图像，固定雨核 $C_n$ ，问题的关键是准确估计 $M_ns$ 和 $B$ 。优化问题可以被表示为：

$\min _{\mathcal{M}, \mathcal{B}}\left\|\mathcal{O}-\mathcal{B}-\sum_{n=1}^{N} \mathcal{C}_{n} \otimes \boldsymbol{M}_{n}\right\|_{F}^{2}+\alpha g_{1}(\mathcal{M})+\beta g_{2}(\mathcal{B})$

其中， $\mathcal{M}$ 是来自 $M_ns$ 的张量， $g1$ 和 $g2$ 是用于保留先验结构信息的正则项。

估计雨图M与背景B¶

作者采用一种多个重复的成对子网络组合来构成多阶段的架构设计，整体的架构设计在下一节解释，先解释一下单个阶段的成对子网络设计和网络设计后的解释性原理。

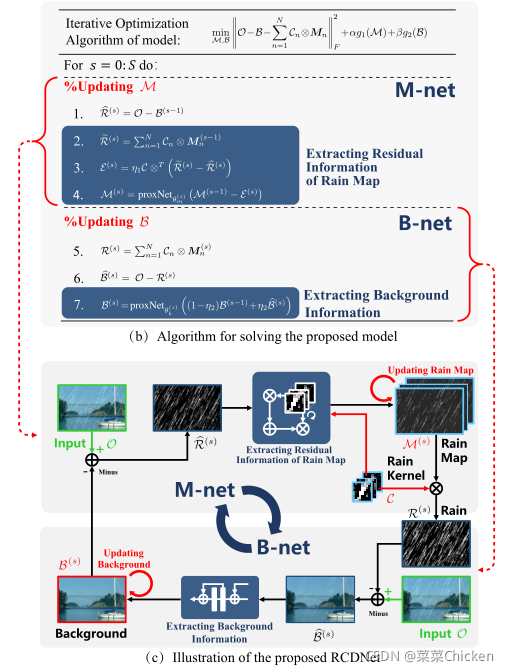
子网络示意图，图片来自原论文

上图中，估计雨图的部分即M-net，估计背景的部分即B-net，箭头指向对应的网络。通过求解优化问题表示式的二次逼近，雨图更新式可以表示为：

$\min _{\mathcal{M}} \frac{1}{2}\left\|\mathcal{M}-\left(\mathcal{M}^{(s-1)}-\eta_{1} \nabla f\left(\mathcal{M}^{(s-1)}\right)\right)\right\|_{F}^{2}+\alpha \eta_{1} g_{1}(\mathcal{M})$

其中， $\mathcal{M}^{(s-1)}$ 为上一阶段的更新结果。 $\eta_{1}$ 为步长参数

$f(\mathcal{M}^{(s-1)}) = \left\|\mathcal{O}-\mathcal{B}^{(s-1)}-\sum_{n=1}^{N} \mathcal{C}_{n} \otimes \boldsymbol{M}_{n}^{(s-1)}\right\|_{F}^{2}$ 。

与一般的正则项对应，上式的解为：

$\mathcal{M}^{(s)}=\operatorname{prox}_{\alpha \eta_{1}}\left(\mathcal{M}^{(s-1)}-\eta_{1} \nabla f\left(\mathcal{M}^{(s-1)}\right)\right)$

我们将下式代入上式中：

$\nabla f\left(\mathcal{M}^{(s-1)}\right)=\mathcal{C} \otimes^{T}\left(\sum_{n=1}^{N} \mathcal{C}_{n} \otimes \boldsymbol{M}_{n}^{(s-1)}+\mathcal{B}^{(s-1)}-\mathcal{O}\right)$

式中的 $\mathcal{C} \in \mathbb{R}^{k \times k \times N \times 3}$ 是一个4维张量， $\otimes^{T}$ 表示转置卷积，最终我们可以获得雨图M的更新式：

$\begin{aligned} &\mathcal{M}^{(s)}= &\operatorname{prox}_{\alpha \eta_{1}}\left(\mathcal{M}^{(s-1)}-\eta_{1} \mathcal{C} \otimes^{T}\left(\sum_{n=1}^{N} \mathcal{C}_{n} \otimes \boldsymbol{M}_{n}^{(s-1)}+\mathcal{B}^{(s-1)}-\mathcal{O}\right)\right) \end{aligned}$

其中， $\operatorname{prox}_{\alpha \eta_{1}}(\cdot)$ 是依赖于正则项 $g1$ ，关于 $\mathcal{M}$ 的近似更新函数。

同理，关于背景 $\mathcal{B}$ 的二次逼近为：

$\min _{\mathcal{B}} \frac{1}{2}\left\|\mathcal{B}-\left(\mathcal{B}^{(s-1)}-\eta_{2} \nabla h\left(\mathcal{B}^{(s-1)}\right)\right)\right\|_{F}^{2}+\beta \eta_{2} g_{2}(\mathcal{B})$

其中

$\nabla h\left(\mathcal{B}^{(s-1)}\right)=\sum_{n=1}^{N} \mathcal{C}_{n} \otimes \boldsymbol{M}_{n}^{(s)}+\mathcal{B}^{(s-1)}-\mathcal{O}$

所以可以推出B的最终更新规则为：

$\begin{aligned} &\mathcal{B}^{(s)}= &\operatorname{prox}_{\beta \eta_{2}}\left(\left(1-\eta_{2}\right) \mathcal{B}^{(s-1)}+\eta_{2}\left(\mathcal{O}-\sum_{n=1}^{N} \mathcal{C}_{n} \otimes \boldsymbol{M}_{n}^{(s)}\right)\right) . \end{aligned}$

其中， $\operatorname{prox}_{\alpha \eta_{2}}(\cdot)$ 是依赖于正则项 $g2$ ，关于 $\mathcal{B}$ 的近似更新函数。

雨卷积字典网络¶

受low-level vision task比如反卷积、压缩感知和去雾等中利用的deep unfolding技术的启发，作者将上述方法的每个迭代步骤都展开作为相应的网络模块，从而构建多阶段迭代的可解释去雨网络。

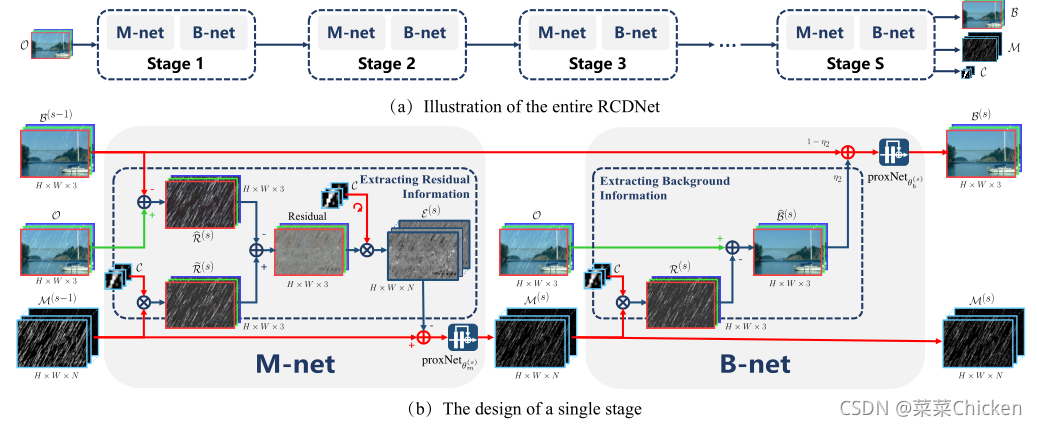
整体框架图，图片来自于原论文

如上图中所示，提出的网络由 $S$ 个阶段组成，对应算法的 $S$ 次迭代步骤。每个阶段通过两个子网络 $\mathcal{M}Net$ 和 $\mathcal{B}Net$ 实现雨图和背景图的更新。在网络的每个阶段，都会把上一个阶段得到的两个输出 $b^{s-1}$ 和 $M{s-1}$ 作为下一阶段的网络输入。展开算法的关键在于我们如何用卷积神经网络去近似关于 $\mathcal{M}$ 和 $\mathcal{B}$ 的更新函数 $\operatorname{prox}_{\alpha \eta_{1}}(\cdot)$ ， $\operatorname{prox}_{\alpha \eta_{2}}(\cdot)$ 。作者使用了ResNet块来近似两个函数，简单来说，首先可以将一个阶段的更新规则分解为多个步骤：

$\mathcal{M}$ ：

$\text { M-net : }\left\{\begin{array}{l} \widehat{\mathcal{R}}^{(s)}=\mathcal{O}-\mathcal{B}^{(s-1)} \\ \widetilde{\mathcal{R}}^{(s)}=\sum_{n=1}^{N} \mathcal{C}_{n} \otimes \boldsymbol{M}_{n}^{(s-1)} \\ \mathcal{E}^{(s)}=\eta_{1} \mathcal{C} \otimes^{T}\left(\tilde{\mathcal{R}}^{(s)}-\widehat{\mathcal{R}}^{(s)}\right) \\ \mathcal{M}^{(s)}=\operatorname{proxNet}_{\theta_{m}^{(s)}}\left(\mathcal{M}^{(s-1)}-\mathcal{E}^{(s)}\right) \end{array}\right.$

$\mathcal{B}$ ：

$\text { B-net : }\left\{\begin{array}{l} \mathcal{R}^{(s)}=\sum_{n=1}^{N} \mathcal{C}_{n} \otimes \boldsymbol{M}_{n}^{(s)} \\ \widehat{\mathcal{B}}^{(s)}=\mathcal{O}-\mathcal{R}^{(s)} \\ \mathcal{B}^{(s)}=\operatorname{prox} \operatorname{Net}_{\theta_{b}^{(s)}}\left(\left(1-\eta_{2}\right) \mathcal{B}^{(s-1)}+\eta_{2} \widehat{\mathcal{B}}^{(s)}\right) \end{array}\right.$

$\operatorname{prox}_{\alpha \eta_{1}}(\cdot)$ ， $\operatorname{prox}_{\alpha \eta_{2}}(\cdot)$ 由多个级联的resnet块组成，参数分别为： $\theta_b^s$ 和 $\theta_m^s$ 。雨核 $\mathcal{C}_{n}$ , $\theta_b^s$ 和 $\theta_m^s$ 等都从数据中自动学习得来。

作者巧妙的思路和推导使得两个子网络都有着很健壮的解释性，如上图中所示， $\mathcal{M}Net$ 首先通过上一阶段估计得到的背景与原图，得到雨层，当前阶段的雨层 $\widehat{\mathcal{R}}^{(s)}$ ，雨核与上一阶段的雨图利用转置卷积求得雨层 $\widetilde{\mathcal{R}}^{(s)}$ ，二者相减，从而计算出两个雨图的残差信息。接下来， $\mathcal{B}Net$ 利用当前阶段的雨核和雨图恢复出背景图，并用可训练参数 $\eta_{2}$ 做了一个上一阶段输出的 $B$ 和当前阶段计算出的 $B$ 的融合结果图作为当前阶段 $B$ 的更新结果送入残差网络 $\operatorname{prox}_{\alpha \eta_{2}}(\cdot)$ ：

$\mathcal{B}^{(s)} = \eta_{2} \mathcal{B}^{(s-1)} + (1- \eta_{2})\widehat{\mathcal{B}}^{(s)}$

Loss function¶

作者采用了每个阶段学习的背景和雨层的均方误差作为训练目标函数:

$L=\sum_{s=0}^{S} \lambda_{s}\left\|\mathcal{B}^{(s)}-\mathcal{B}\right\|_{F}^{2}+\sum_{s=1}^{S} \gamma_{s}\left\|\mathcal{O}-\mathcal{B}-\mathcal{R}^{(s)}\right\|_{F}^{2}$

指标结果¶

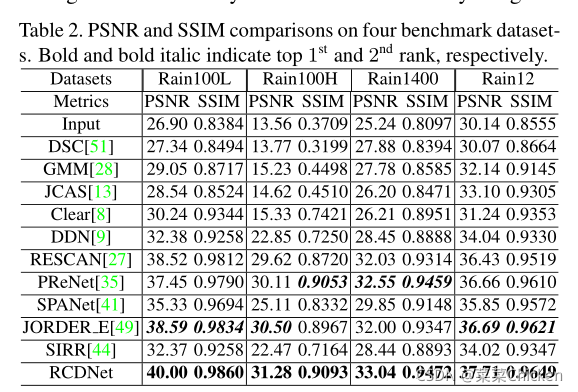
paper中展示了常用的几个数据集上的指标结果，指标非常不错。

指标对比图，图片来自论文原文

效果图展示¶

合成数据集上：

合成数据集上的效果对比图，图片来自原论文

真实雨图上：

真实雨图上的效果对比图，测试图来自互联网，图片来自论文原文。

结论¶

作者提出了一种利用雨条纹的内在先验结构的可解释网络，网络中的每个模块都可以与求解模型中一一对应而实现，网络不再是黑盒子了，变成了每一模块都能观察、分析的白盒子~让人感觉眼前一亮，非常值得细细学习和分析。

本文总阅读量次