前言¶

昨天盘点了一下目标检测算法的常见数据集还有评判标准，但目标检测过程还有一个后处理算法的重要性确常被忽略，今天我们就来盘点一下目标检测算法中的NMS相关知识吧。

NMS¶

介绍¶

非极大值抑制(Non-Maximum Suppression，NMS)，顾名思义就是抑制不是极大值的元素。在目标检测任务，例如行人检测中，滑动窗口经过特征提取和分类器识别后，每个窗口都会得到一个分数。但滑动窗口会导致很多窗口和其它窗口存在包含大部分交叉的情况。这个时候就需要用到NMS来选取那些邻域里分数最高，同时抑制那些分数低的窗口。

原理¶

在目标检测任务中，定义最后的候选框集合为 $B$ ，每个候选框对应的置信度是 $S$ ，IOU阈值设为 $T$ ，然后NMS的算法过程可以表示如下：

选择具有最大score的候选框 $M$
将 $M$ 从集合 $B$ 中移除并加入到最终的检测结果 $D$ 中
将 $B$ 中剩余检测框中和 $M$ 的交并比(IOU，昨天的推文有介绍)大于阈值 $T$ 的框从B中移除
重复上面的步骤，直到 $B$ 为空

代码实现¶

rgb大神实现Faster-RCNN中的单类别物体nms代码解释如下：

# --------------------------------------------------------
# Fast R-CNN
# Copyright (c) 2015 Microsoft
# Licensed under The MIT License [see LICENSE for details]
# Written by Ross Girshick
# --------------------------------------------------------

import numpy as np

def py_cpu_nms(dets, thresh):
    """Pure Python NMS baseline."""
    #x1、y1、x2、y2、以及score赋值
    x1 = dets[:, 0]
    y1 = dets[:, 1]
    x2 = dets[:, 2]
    y2 = dets[:, 3]
    scores = dets[:, 4]
    #每一个检测框的面积
    areas = (x2 - x1 + 1) * (y2 - y1 + 1)
    #按照score置信度降序排序
    order = scores.argsort()[::-1]
    #保留的结果框集合
    keep = []
    while order.size > 0:
        i = order[0]
        #保留该类剩余box中得分最高的一个
        keep.append(i)
        # 得到相交区域,左上及右下
        xx1 = np.maximum(x1[i], x1[order[1:]])
        yy1 = np.maximum(y1[i], y1[order[1:]])
        xx2 = np.minimum(x2[i], x2[order[1:]])
        yy2 = np.minimum(y2[i], y2[order[1:]])
        #计算相交的面积,不重叠时面积为0
        w = np.maximum(0.0, xx2 - xx1 + 1)
        h = np.maximum(0.0, yy2 - yy1 + 1)
        inter = w * h
        #计算IoU：重叠面积 /（面积1+面积2-重叠面积）
        ovr = inter / (areas[i] + areas[order[1:]] - inter)
        # 保留IoU小于阈值的box
        inds = np.where(ovr <= thresh)[0]
        # 因为ovr数组的长度比order数组少一个,所以这里要将所有下标后移一位
        order = order[inds + 1]

    return keep

效果¶

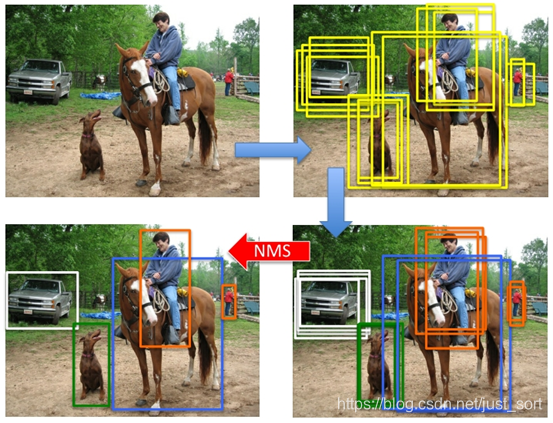
在这里插入图片描述

Soft-NMS¶

上面说的NMS算法有一个缺点就是当两个候选框的重叠度很高时，NMS会将具有较低置信度的框去掉，也就是将其置信度变成0，如下图所示，红色框和绿色框是当前的检测结果，二者的得分分别是0.95和0.80。如果按照传统的NMS进行处理，首先选中得分最高的红色框，然后绿色框就会因为与之重叠面积过大而被删掉。

在这里插入图片描述

因此为了改善这个缺点，Soft-NMS被提出，核心思路就是不要粗鲁地删除所有IOU大于阈值的框，而是降低其置信度。这个方法的论文地址为：https://arxiv.org/pdf/1704.04503.pdf 。算法伪代码如下：

在这里插入图片描述

正如作者所说，改一行代码就OK了。这里的 $f$ 函数可以是线性函数，也可以是高斯函数。我们来对比一下： - 线性函数：

$s_i=\begin{cases} s_i, && \text{iou}( \mathcal M,b_i) < N_t \\ s_i(1-\text{iou}(\mathcal M,b_i)), && \text{iou}(\mathcal M,b_i)\ge N_t \end{cases}$

高斯函数： $<span><span class="MathJax_Preview">s_i=s_ie^{-{\text{iou}(\mathcal M,b_i)^2}\over \sigma},\forall b_i\not \in \mathcal D</span><script type="math/tex">s_i=s_ie^{-{\text{iou}(\mathcal M,b_i)^2}\over \sigma},\forall b_i\not \in \mathcal D$

代码实现¶

作者的代码如下：

def cpu_soft_nms(np.ndarray[float, ndim=2] boxes, float sigma=0.5, float Nt=0.3, float threshold=0.001, unsigned int method=0):
    cdef unsigned int N = boxes.shape[0]
    cdef float iw, ih, box_area
    cdef float ua
    cdef int pos = 0
    cdef float maxscore = 0
    cdef int maxpos = 0
    cdef float x1,x2,y1,y2,tx1,tx2,ty1,ty2,ts,area,weight,ov

    for i in range(N):
        maxscore = boxes[i, 4]
        maxpos = i

        tx1 = boxes[i,0]
        ty1 = boxes[i,1]
        tx2 = boxes[i,2]
        ty2 = boxes[i,3]
        ts = boxes[i,4]

        pos = i + 1
    # get max box
        while pos < N:
            if maxscore < boxes[pos, 4]:
                maxscore = boxes[pos, 4]
                maxpos = pos
            pos = pos + 1

    # add max box as a detection 
        boxes[i,0] = boxes[maxpos,0]
        boxes[i,1] = boxes[maxpos,1]
        boxes[i,2] = boxes[maxpos,2]
        boxes[i,3] = boxes[maxpos,3]
        boxes[i,4] = boxes[maxpos,4]

    # swap ith box with position of max box
        boxes[maxpos,0] = tx1
        boxes[maxpos,1] = ty1
        boxes[maxpos,2] = tx2
        boxes[maxpos,3] = ty2
        boxes[maxpos,4] = ts

        tx1 = boxes[i,0]
        ty1 = boxes[i,1]
        tx2 = boxes[i,2]
        ty2 = boxes[i,3]
        ts = boxes[i,4]

        pos = i + 1
    # NMS iterations, note that N changes if detection boxes fall below threshold
        while pos < N:
            x1 = boxes[pos, 0]
            y1 = boxes[pos, 1]
            x2 = boxes[pos, 2]
            y2 = boxes[pos, 3]
            s = boxes[pos, 4]

            area = (x2 - x1 + 1) * (y2 - y1 + 1)
            iw = (min(tx2, x2) - max(tx1, x1) + 1)
            if iw > 0:
                ih = (min(ty2, y2) - max(ty1, y1) + 1)
                if ih > 0:
                    ua = float((tx2 - tx1 + 1) * (ty2 - ty1 + 1) + area - iw * ih)
                    ov = iw * ih / ua #iou between max box and detection box

                    if method == 1: # linear
                        if ov > Nt: 
                            weight = 1 - ov
                        else:
                            weight = 1
                    elif method == 2: # gaussian
                        weight = np.exp(-(ov * ov)/sigma)
                    else: # original NMS
                        if ov > Nt: 
                            weight = 0
                        else:
                            weight = 1

                    boxes[pos, 4] = weight*boxes[pos, 4]

            # if box score falls below threshold, discard the box by swapping with last box
            # update N
                    if boxes[pos, 4] < threshold:
                        boxes[pos,0] = boxes[N-1, 0]
                        boxes[pos,1] = boxes[N-1, 1]
                        boxes[pos,2] = boxes[N-1, 2]
                        boxes[pos,3] = boxes[N-1, 3]
                        boxes[pos,4] = boxes[N-1, 4]
                        N = N - 1
                        pos = pos - 1

            pos = pos + 1

    keep = [i for i in range(N)]
    return keep

效果¶

在这里插入图片描述左边是使用了NMS的效果，右边是使用了Soft-NMS的效果。

论文的实验结果¶

在这里插入图片描述可以看到在MS-COCO数据集上map$[0.5:0.95]可以获得大约1%的提升，如果应用到训练阶段的proposal选取过程理论上也能获得提升。顺便说一句，soft-NMS在不是基于Proposal的方法如SSD,YOLO中没什么提升。这里猜测原因可能是因为YOLO和SSD产生的框重叠率较低引起的。

后记¶

今天介绍了目标检测任务中的后处理过程最重要的NMS算法以及它的改进方案Soft-NMS算法，并提供了实现源码，希望大家能彻底理解这两个算法。

思考¶

NMS的阈值是否可以自适应？

欢迎关注我的微信公众号GiantPadaCV，期待和你一起交流机器学习，深度学习，图像算法，优化技术，比赛及日常生活等。

图片.png

本文总阅读量次