前言¶

这是卷积神经网络学习路线的第一篇文章，这篇文章主要为大家介绍卷积神经网络的组件以及直观的为大家解释一下卷积层是如何在图像中发挥作用的。

卷积神经网络的组件¶

从AlexNet在2012年ImageNet图像分类识别比赛中以碾压性的精度夺冠开始，卷积神经网络就一直流行到了现在。现在，卷积神经网络已经被广泛的应用在了图像识别，自然语言处理，语音识别等领域，尤其在图像识别中取得了巨大的成功。本系列就开始带大家一起揭开卷积神经网络的神秘面纱，尝试窥探它背后的原理。卷积神经网络的组件有输入层，卷积层，激活层，池化层，全连接层。

输入层¶

输入层(Input Layer)是将原始数据或者其他算法预处理后的数据输入到卷积神经网络，数据没有明确定义，可以是数字图像，可以是音频识别领域经过傅里叶变换的二维波形数据，也可以是自然语言处理中一维表示的句子向量。输入层的作用是将输入数据送入卷积神经网络进行特征提取，然后获得我们想要的结果。同时根据计算能力差异，机器存储能力差异和模型参数多少可以控制输入不同数量的数据。也就是我们常说的$batchsize$。

卷积层¶

卷积层(Convolution Layer)是卷积神经网络的核心组件，它的作用通常是对输入数据进行特征提取，通过卷积核矩阵对原始数据中隐含关联性进行抽象。原始的二维卷积算子的公式如下：

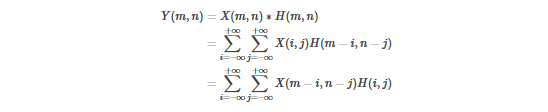
其中，$H(m, n)$表示卷积核，$X(m, n)$表示输入到卷积层的特征图。和原始的二维卷积算子不同，卷积神经网络首先是维度升至三维、四维卷积，跟二维卷积相比多了一个“通道”(channel)，每个通道还是按照二维卷积方式计算，而多个通道与多个卷积核分别进行二维卷积，得到多通道输出，需要“合并”为一个通道；其次是卷积核在卷积计算时没有“翻转”，而是与输入图片做滑动窗口“相关”计算。用公式重新表达如下：

$Y^l(m,n) =X^k(m,n)*H^{kl}(m,n) = \sum_{k=0}^{K-1}\sum_{i=0}^{I-1}\sum_{j=0}^{J-1}X^k(m+i,n+j)H^{kl}(i,j)$

这里假定卷积神经网络有$K$个输入通道和$L$个输出通道，所以一共需要$K\times L$个卷积核来实现通道数目的变换。从左到右看，$Y^l$表示第$l$个输出通道的二维特征图，$X^k$表示第$k$个输入通道的二维特征图，$H^{kl}$表示第$k$个卷积核的第$l$个通道。设卷积核大小是$I\times J$，每个输出通道的特征图大小是$M\times N$，则该层每个样本做一次前向传播时卷积层的计算量(Calculations)是$MAC=I\times J\times M\times N\times K\times L$。而卷积核的学习参数(Params)为$I\times J\times K\times L$。定义卷积层的计算量核参数量比值为$CPR=Calculations/Params=M\times N$。从这里可以看出，卷积层的输出特征图分辨率越大，CPR越高，也即是说参数利用率越高。

总结一下，卷积层的优点在于局部连接（有助于减少参数量）和权值共享。我们分别来举例说明一下：

• 局部连接 ：假设现在输入图片分辨率是100*100，然后隐藏层神经元有10^5个，如果全连接的话，那么每个隐藏层神经元都连接图像的一个像素点，就有$10^9$个连接，这个参数量是很大的。对于卷积层来讲，如果卷积核大小为$3\times 3$那么每个神经元只需要和原始图像中的一个$3\times 3$的局部区域连接，所以一共只有$9\times 10^5$个连接。可以看到通过局部连接，卷积层的参数量减少了很多。
• 权值共享：在上面的局部连接中，一个有$9\times 10^5$个参数。如果每个神经元对应的参数都相同的话，那么需要训练的参数实际上就只有$9$个了。这个就是$3\times 3$的卷积核。而权值共享的意思就是训练好的一个$3\times 3$卷积核表示了在图像中提取某种特征的能力，例如提取人脸上的眼睛，也就是说卷积核具有了这种能力，无论在图像的哪个地方都可以起作用。这只是一个卷积核的作用，作用肯定是有限的，那么如果我们用100个卷积核来提取特征，那么特征提取能力就会大大增强。同时参数两也不过才$3\times 3\times 100$。所以是非常cheap并且effective的。

激活层¶

激活层(Activation Layer)负责对卷积层抽取的特诊进行激活，由于卷积操作是把输入图像和卷积核进行相应的线性变换，需要引入激活层(非线性函数)对其进行非线性映射。激活层由非线性函数组成，常见的如$sigmoid$，$tanh$，$relu$。最常用的激活函数是$ReLU$，又叫线性整流器。公式表达为： $f(x)=\begin{cases} 0 & if& x<0 \\ x & if & x>=0\end{cases}$

池化层¶

所谓池化层(Pooling)就是将特征图下采用，作用是对感受域内的特征进行筛选，提取区域内最具代表性的特征，能够有效地降低输出特征尺度，进而减少模型所需要的参数量。按操作类型通常分为最大池化(Max Pooling)、平均池化(Average Pooling)和求和池化(Sum Pooling)，它们分别提取感受域内最大、平均与总和的特征值作为输出，最常用的是最大池化，也即是MaxPooling。根据相关研究，特征提取的误差主要来自于两点：

• 邻域大小受限造成的估计值方差增大。
• 卷积层参数误差造成估计均值的偏移。

一般来说，平均池化可以减少第一种误差，更多的保留图像的背景信息，而最大池化可以降低第二种误差，更多的保留图像的纹理信息。 总结一下，池化层优点有：

• 不变性，更关注是否存在某些特征而不是特征具体的位置。可以看作加了一个很强的先验，让学到的特征要能容忍一些的变化。（实际上这个容忍能力是非常有限的）
• 减少下一层输入大小，减少计算量和参数量。
• 获得定长输出。（文本分类的时候输入是不定长的，可以通过池化获得定长输出）
• 防止过拟合或有可能会带来欠拟合。

说了这么多池化的优点，那么它有什么缺点吗？ - 语义分割任务中，多次下采样会使得图像中某些目标细节丢失，结果不精细。

南大的一维物理学硕士在知乎上发表了一篇文章，题为CNN真的需要下采样（上采样）吗?大家可以看看，文章地址是：https://zhuanlan.zhihu.com/p/94477174。

全连接层¶

全连接层(Full Connected Layer)就是一个线性特征映射的过程，将多维的特征输入映射为二维的特征输出，高维表示样本批次($batchsize$)，低位常常对应任务目标(例如分类就对应每一个类别的概率)。

卷积层是如何在图像中起作用的？¶

首先说，这一部分基本看下面这篇论文就足够了。地址为：https://arxiv.org/abs/1311.2901 。想了解每个卷积层学到了什么，一个常见的想法就是把特征图可视化出来。那么怎么可视化呢？介绍一下论文的方法。

首先下面表示尺寸为$224\times 224$原图经过一个卷积层再经过ReLU处理，最后再经过一个步长为$2$的池化层变成了维度为$112\times 112\times 96$的特征图。

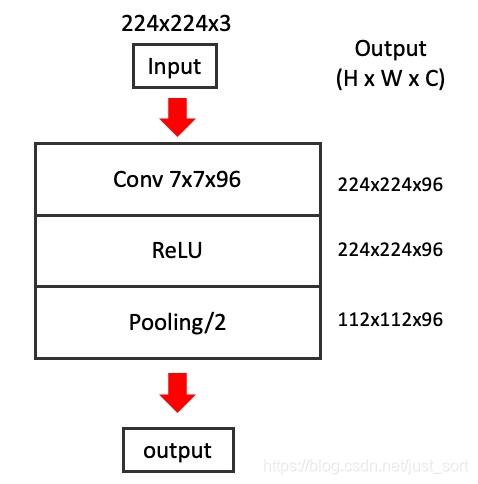
现在我们的目标是要可视化这个$112\times 112\times 96$的特征图，一个直观的想法是将$112\times 112\times 96$的特征图选定$1$个特征图保留，其他$95$个都置0，然后原路反操作回Input，再将像素反normalize到0-255范围，我们观察这个图像就可以了。这个过程可以用下图表示：

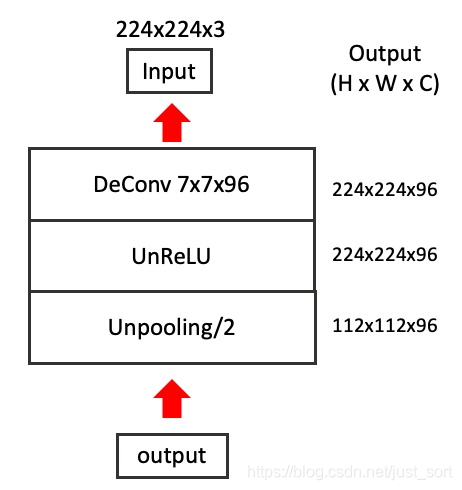
所以整个问题的关键就在于如何反卷积，反池化，以及反ReLU。反ReLU比较简单，就不说了。对于反Conv，论文用转置卷积代替了。由于后面的专栏会专门将转置卷积这里就不多说了。Unpooling要创意在于Pooling过程中，需要记录下Pooling后的每个数据的来源位置，在Unpooling过程中，按位置，将数据还原，其他补零。

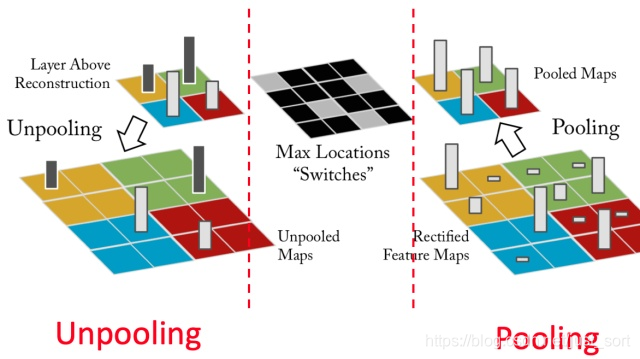
有了上诉操作，我们就可以获得每个feature map对应的原图了。下图给出了ZFNet的第三个卷积层随机挑选的12个feature map，在校验集上top9的激活值的可视化，右边是对应的原始输入图片。

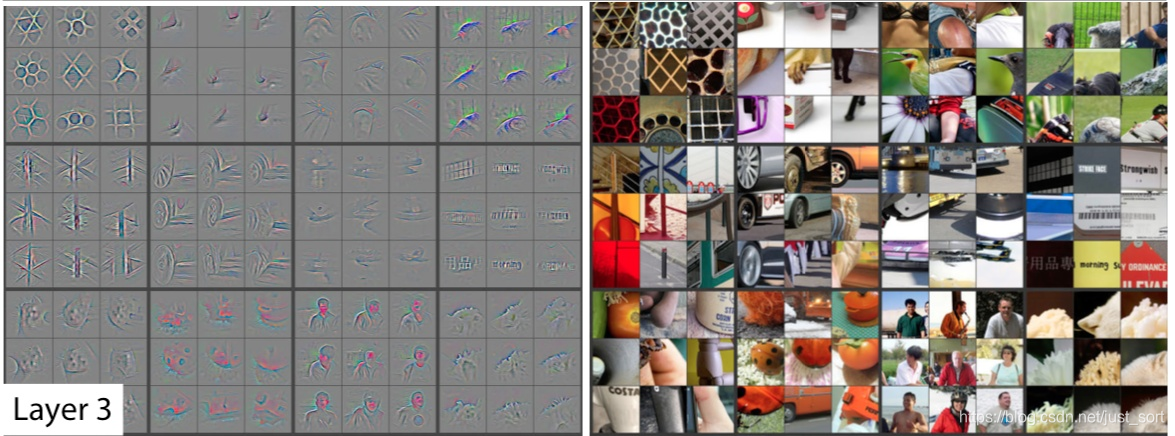
明显的一个feature map学习到的特征比较相似。而且都学习到了主要特征。其他细节请看论文。这里还有一个视频讲解这个论文的可视化过程和论文的一些细节，例如反卷积，池化，ReLU是分别如何实现的，但我上传不了，可以到我的公众号后台回复"视频"获取。

后记¶

本节是卷积神经网络学习路线（一），主要讲了卷积神经网络的组件以及卷积层是如何在图像中起作用的？希望对大家有帮助。

参考文章¶

https://zhuanlan.zhihu.com/p/82850456 https://blog.csdn.net/lc013/article/details/80237632

欢迎关注我的微信公众号GiantPandaCV，期待和你一起交流机器学习，深度学习，图像算法，优化技术，比赛及日常生活等。